1、单选题  某单位订阅了30份学习材料发放给3个部门，每个部门至少发放9份材料。问一共有多少种不同的发放方法?_____
A: 7
B: 9
C: 10
D: 12
参考答案: C
本题解释:正确答案是C考点排列组合问题解析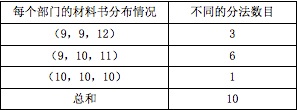

2、单选题  某高校从E、F和G三家公司购买同一设备的比例分别是20%、40%和40%，E、F和G三家公司所生产设备的合格率分别是98%、98%和99%，现随机购买到一台次品设备的概率是_____。
A: 0.013
B: 0.015
C: 0.016
D: 0.01
参考答案: C
本题解释:正确答案是C考点概率问题解析买到次品的概率为20%×2%+40%×20%+40%×1%=0.016，故正确答案为C。

3、单选题  有一排长椅总共有65个座位，其中已经有些座位上有人就坐。现在又有一人准备找一个位置就坐，但是此人发现，无论怎么选择座位，都会与已经就坐的人相邻。问原来至少已经有多少人就坐?_____
A: 13
B: 17
C: 22
D: 33
参考答案: C
本题解释:正确答案是C考点抽屉原理问题解析分析一下，无论怎么选择座位，都会与已经就坐的人相邻，意味着，长椅两端最靠边的位置上最多只空了1个座位，而中间人与人之间最多只空了2个座位。从至少已经有多少人就坐有角度来看，假设第2个座位上有人的话，第5、8、11……62、65个座位分别有人，这样的结果需要人最少。从总人数来说，也就是说每3个位置坐1人，所以很显然是22人，故正确答案为C。

4、单选题  共有20个玩具交给小王手工制作完成。规定，制作的玩具每合格一个得5元，不合格一个扣2元，未完成的不得不扣。最后小王共收到56元，那么他制作的玩具中，不合格的共有_____个。
A: 2
B: 3
C: 5
D: 7
参考答案: A
本题解释:正确答案是A考点不定方程问题解析设小王制作合格玩具x个，不合格玩具y个，未完成的有z个。则x+y+z=20，5x-2y=56。为不定方程组，将选项代入验证，仅当y=2时，x与z有正整数解。故正确答案为A。

5、单选题  某礼堂的观众座椅共96张，分东、南、西三个区域摆放。现从东区搬出与南区同样多的座椅放倒南区，再从南区搬出与西区同样多的座椅放到西区，最后从西区搬出与东区剩下的座椅数量相同的座椅放到东区，这时三个区域的座椅数量相同。则最初南区的座椅有_____张。
A: 24
B: 28
C: 32
D: 36
参考答案: B
本题解释:正确答案是B考点统筹规划问题解析第一次搬：东-南，2南，西;第二次搬：东-南，2南-西，2西;第三次搬：2东-2南，2南-西，2西-东+南。2东-2南=2南-西=2西-东+南，解得4南=7西，则南区座椅数肯定为7的倍数，只有B符合条件。故正确答案为B。标签数字特性