1、单选题  A、B、C、D、E是5个不同的整数，两两相加的和共有8个不同的数值，分别是17、25、28、31、34、39、42、45，则这5个数中能被6整除的有几个?_____
A: 4
B: 1
C: 2
D: 3
参考答案: C
本题解释:正确答案是C考点趣味数学问题解析设A<B<C<D<E，则必有A+B=17，A+C=25，C+E=42，D+E=45。两两相加，应该有10个数值，因此必有两个重复值。这10个数值相加，必为4的倍数，将题中8个数值相加得261，除以4余1，因此另外两个加和必然除以4余3，重复的两个数在28、31、34、39中，因此这两个数为28、39或28、31，28必为重复值，可知B+C=A+D=28，所以，A=7，B=10，C=18，D=21，E=24，能被6整除的有18、24两个。故正确答案为C。

2、单选题  自然数P满足下列条件：P除以10的余数为9，P除以9的余数为8，P除以8的余数为7。如果：100＜P＜1000，则这样的P有几个？_____
A: 不存在
B: 1个
C: 2个
D: 3个
参考答案: C
本题解释:正确答案是C解析由"除以10的余数为9，P除以9的余数为8，P除以8的余数为7"，满足差同减差，对应口诀可知其符合表达式为360n－1，由于100＜P＜1000，则100＜360n－1＜1000，所以n能取1、2，则满足条件的P有两个，即359和719，故正确答案为C。注释：同余问题需要掌握如下口诀：余同取余，和同加和，差同加差，最小公倍数做周期。口诀解释：余同取余，例如"一个数除以7余1，除以6余1，除以5余1"，可见所得余数恒为1，则取1，被除数的表达式为210n＋1；和同加和，例如"一个数除以7余1，除以6余2，除以5余3"，可见除数与余的和相同，取此和8，被除数的表达式为210n＋8；差同减差，例如"一个数除以7余3，除以6余2，除以5余1"，可见除数与余的差相同，取此差4，被除数的表达式为210n－4。特别注意前面的210是5、6、7的最小公倍数。余数与同余问题标签同余问题

3、单选题  某单位有3项业务要招标，共有5家公司前来投标、且每家公司都对3项业务发出了投标申请，最终发现每项业务都有且只有1家公司中标。如5家公司在各项业务中中标的概率均相等，问这3项业务由同一家公司中标的概率为多少：_____
A: 1/25
B: 1/81
C: 1/125
D: 1/243
参考答案: A
本题解释:正确答案是A，解析:根据概率的定义：所求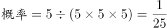

4、单选题  小张在做一道除法时，误将除数45看成54，结果得到的商是3，余数是7。问正确的商和余数之和是_____。
A: 11
B: 18
C: 26
D: 37
参考答案: D
本题解释:正确答案是D考点余数与同余问题解析由题意，被除数=54×3+7=169，于是正确的除法过程为169÷45=3••••••34，正确的商与余数之和为37。故正确答案为D。

5、单选题  小王和小张各加工了10个零件，分别有1个和2个次品。若从两人加工的零件里各随机选取2个，则选出的4个零件中正好有1个次品的概率为_____。
A: 小于25%
B: 25%-35%
C: 35%-45%
D: 45%以上
参考答案: C
本题解释:正确答案是C，全站数据:本题共被作答1次，正确率为100.00%解析由于只有1个次品，那么次品归属为谁，就应该分两种情况讨论。第一种情况，次品为小王的。那么从小王的9个正品选1个再从1个次品中选一个有C(1，9)×C(1，1)=9种情况，从小李的8个正品中选2个有C(2，8)=28种情况，两者相乘为252;第二种情况，次品为小李的。那么从小李的8个正品选1个再从2个次品中选一个有C(1，8)×C(1，2)=16种情况，从小王的9个正品中选2个有C(2，9)=36种情况，两者相乘为576;所以最终将2种情况相加得到828种情况。再计算总的情况，每人都从10个里面取2个有C(2，10)=45种情况，所以两者相乘一共有45×45=2025中情况，最后用828÷2025，估算得到C。故正确答案为C。速解本题主要考察排列组合的分类计算的思想。对于概率问题，一般都是用：(满足条件的特点排列组合数)÷(全部情况的排列组合数)考点排列组合问题概率问题笔记编辑笔记