1、单选题  有一条公路长900米，在公路的一侧从头到尾每隔10米栽一根电线杆，可栽多少根电线杆?_____。
A: 82
B: 76
C: 91
D: 102
参考答案: C
本题解释:参考答案:C
题目详解:根据题意，公路全长可以分成若干段，由于公路的两端都要求栽杆，这是植树问题的变形，为两端均植树问题。确定总长：900确定间距：10带入两端均植树问题的公式：棵数=总长÷间距+1=900÷10+1=91所以，选C。考查点:数量关系>数学运算>特殊情境问题>植树问题>两端均植树

2、单选题  如下图所示，街道ABC在B处拐弯，在街道一侧等距装路灯，要求A、B、C处各装一盏路灯，这条街道最少装多少盏路灯?_____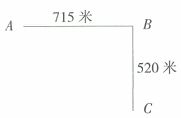A: 18
B: 19
C: 20
D: 21
参考答案: C
本题解释:参考答案:C
题目详解:根据题意，要求的是最少装灯的数量且路等间距相等，可知A--B和B--C间路灯的间距得相等;所以要求先715和520的最大公约数，715=5×11×13，

3、单选题  (2005广东下，第11题)要在一块边长为48米的正方形地里种树苗，已知每行相距3米，每竖列相距6米，四角各种一棵树，问一共可种多少棵树苗?_____
A: 128棵
B: 132棵
C: 153棵
D: 157棵
参考答案: C
本题解释:参考答案:C
题目详解:根据“每横行相距3米”、“四角各种一棵树”可知，应使用不封闭植树理论，且为两端均植树问题。两端均植树：点数=总长÷间距+1确定总长：48确定间距：3带入公式：点数=总长÷间距+1=48÷3+1=17根据“每竖列相距6米”，“四角各种一棵树”可知，应使用不封闭植树理论，且为两端均植树问题。两端均植树：点数=总长÷间距+1确定总长：48确定间距：6带入公式：点数=总长÷间距+1=48÷6+1=9总可种树：17×9=153棵。因此，选C。考查点:数量关系>数学运算>特殊情境问题>植树问题>两端均植树

4、单选题  某人要上某大厦的10楼，他从1楼到5楼用了100秒，按此速度，他到10楼还需要的时间为_____秒。
A: 225
B: 125
C: 100
D: 150
参考答案: B
本题解释:参考答案:B
题目详解:从1楼到5楼共有5-1=4段楼梯，每层楼梯花了100÷4=25秒。从5楼到10楼共有10-5=5段楼梯，从5楼道10楼需要时间为：25×5=125秒。考查点:数量关系>数学运算>特殊情境问题>植树问题>两端均植树

5、单选题  (2008山东，第41、2005广东下，第12题)把一根钢管锯成5段需要8分钟，如果把同样的钢管锯成20段需要多少分钟?_____
A: 32分钟
B: 38分钟
C: 40分钟
D: 152分钟
参考答案: B
本题解释:参考答案:B
题目详解:根据题意，画出5段钢管示意图，可知：A-----B------C------D------F------G把一根钢管锯成5段，实际只要锯4次就行;也就是说锯4次需要8分钟，所以每次需要8÷4=2分钟;20段需要锯19次，所以需要2×19=38分钟。所以，选B。考查点:数量关系>数学运算>特殊情境问题>植树问题>两端均不植树