1、单选题  如图，甲、乙、丙、丁四个长方形拼成正方形EFGH，中间阴影为正方形。已知，甲、乙、丙、丁四个长方形面积的和是32cm2，四边形ABCD的面积是20cm2。问甲、乙、丙、丁四个长方形周长的总和是_____。 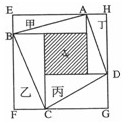A: 32cm
B: 56cm
C: 48cm
D: 68cm
参考答案: C
本题解释:正确答案是C考点几何问题解析根据已知，四边形ABCD的面积为甲、乙、丙、丁四个长方形面积的一半加上阴影部分小正方形的面积，所以小正方形的面积为20-32×1/2=4，正方形EFGH的面积为32+4=36，边长为6，甲、乙、丙、丁四个长方形周长的总和为2×(EA+AH+HD+DG+GC+CF+FB+BE)=2×6×4=48，故正确答案为C。

2、单选题  173×173×173-162×162×162=_____。
A: 926183
B: 936185
C: 926187
D: 926189
参考答案: D
本题解释:D【解析】利用简单的猜测法。173的尾数是3，3的立方为27;162的尾数是2，2立方为8。两者相减尾数为9，所以判断173和162的立方之差的尾数为9。所以答案为D项。

3、单选题  一个自然数，被7除余2，被8除余3，被9除余1，1000以内一共有多少个这样的自然数?_____
A: 5
B: 2
C: 3
D: 4
参考答案: B
本题解释:参考答案:B
题目详解:7、8的最小公倍数为56，根据"差同减差，公倍数做周期"可知：所有满足条件的数可表示为56n-5，也就是除以56余5;要让所有56n-5中满足被9除余1：最小数是n=3时：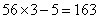

4、单选题  甲乙两个乡村阅览室，甲阅览室科技类书籍数量的1/5相当于乙阅览室该类书籍的1/4，甲阅览室文化类书籍数量的2/3相当于乙阅览室该类书籍的1/6，甲阅览室科技类和文化类书籍的总量比乙阅览室两类书籍的总量多1000本，甲阅览室科技类书籍和文化类书籍的比例为20:1，问甲阅览室有多少本科技类书籍?_____
A: 15000
B: 16000
C: 18000
D: 20000
参考答案: D
本题解释:答案：D.[解析]假设甲阅览室科技类书籍有20x本，文化类书籍有x本，则乙阅读室科技类书籍有16x本，文化类书籍有4x本，由题意有：（20x+x）-（16x+4x）=1000，解出x=1000，则甲阅览室有科技类书籍20000本。

5、单选题  在一个口袋中有l0个黑球、6个白球、4个红球.至少从中取出多少个球才能保证其中有白球? _____
A: 14
B: 15
C: 17
D: 18
参考答案: B
本题解释:【答案】B.解析：抽屉原理，最坏的情况是10个黑球和4个白球都拿出来了，最后第15次拿到的肯定是白球。