1、单选题  某停车场按以下方法收费：每4小时收5元，不足4小时按5元收取，每晚超过零时加收5元，并且每天早上8点开始重新计时，某天下午15时小王将车停入停车场，取车时缴纳停车费65元，小王停车时间t的范围是_____。
A: 如果A、B、P不在同一条直线上，汽车所在位置有3个，可位于A、B两地之间或A、B两地外侧
B: 如果A、B、P不在同一条直线上，汽车的位置有无穷多个
C: 如果A、B、P位于同一条直线上，汽车拉于A、B两地之间或两地外侧
D: 如果A、B、P位于同一条直线上，汽车位于A、B两地外侧，且汽车到A的距离为20千米
参考答案: D
本题解释:正确答案是B考点几何问题解析AB距离为40，AP和BP距离之和为60千米，若A、B、P三点在同一直线上，则P点位于AB外侧10千米处;若A、B、P三点不在同一直线上，则转化为A、B点固定，AP+BP=60即可，有无数种选择。故答案为B。

2、单选题  物美超市的收银台平均每小时有60名顾客前来排队付款，每一个收银台每小时能应付80名顾客付款。某天某时刻，超市如果只开设一个收银台，付款开始4小时就没有顾客排队了，问如果当时开设两个收银台，则付款开始几小时就没有顾客排队了?_____。
A: 2小时
B: 1.8小时
C: 1.6小时
D: 0.8小时
参考答案: D
本题解释:正确答案是D考点牛吃草问题解析假定超市原来排队的人数为N，每小时新增顾客人数为60人，只开1个收银台，4个小时后没有顾客排队，则N=(80×1-60)×4=80(人)。若开两个收银台，则a小时后就没顾客排队，80=(80×2-60)×a，a=0.8，故正确答案为D。

3、单选题  _____ A: A
B: B
C: C
D: D
参考答案: D
本题解释:正确答案是D考点几何问题解析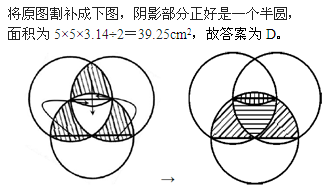

4、单选题  一个正方体木块放在桌子上，每一面都有一个数，位于对面两个数的和都等于13，小张能看到顶面和两个侧面，看到的三个数和为18;小李能看到顶面和另外两个侧面，看到的三个数的和为24，那么贴着桌子的这一面的数是多少?_____
A: 4
B: 5
C: 6
D: 7
参考答案: B
本题解释:正确答案是B考点趣味数学问题解析题目给出对面数字之和为13，则注意将其余条件中出现的对面合在一起。从这一点出发，可以看出若将小张与小王看到的面合在一起，则实际共看到2个顶面与4个不同的侧面。而四个不同侧面恰为两组对面，也即其数字之和为：13×2=26，因此顶面的数字为：(18+24-26)÷2=8，于是底面数字为：13-8=5，故正确答案为B。

5、单选题  有四个自然数A、B、C、D，它们的和不超过400，并且A除以B商是5余5，A除以C商是6余6，A除以D商是7余7。那么，这四个自然数的和是_____。
A: 216
B: 108
C: 314
D: 348
参考答案: C
本题解释:正确答案是C考点余数与同余问题解析由题意可知A=5B+5=6C+6=7D+7，则A为5、6、7的公倍数;5、6、7的最小公倍数为210，根据和不超过400，可知A=210，则可得B=210÷5-1=41、C=210÷6-1=34、D=210÷7-1=29，A+B+C+D=210+41+34+29=314，故正确答案为C。