1、单选题  一只木箱内有白色乒乓球和黄色乒乓球若干个。小明一次取出5个黄球、3个白球，这样操作N次后，白球拿完了，黄球还剩8个；如果换一种取法：每次取出7个黄球、3个白球，这样操作M次后，黄球拿完了，白球还剩24个。原木箱内共有乒乓球多少个？_____
A: 246个
B: 258个
C: 264个
D: 272个
参考答案: C
本题解释:正确答案是C解析乒乓球个数＝（3＋5）×N＋8＝8×（N＋1），即被8整除；乒乓球个数＝（7＋3）×M＋24＝10×（M＋2）＋4，即被10除余4；观察选项，只有C符合要求，故正确答案为C。

2、单选题  下图中的甲和乙都是正方形，BE=6厘米，EF=4厘米。那么，阴影部分ABC的面积是多少平方厘米?_____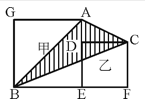A: 20
B: 24
C: 21
D: 18
参考答案: D
本题解释:正确答案是D考点几何问题解析

3、单选题  某市对52种建筑防水卷材产品进行质量抽检，其中有8种产品的低温柔度不合格，10种产品的可溶物含量不达标，9种产品的接缝剪切性能不合格，同时两项不合格的有7种，有1种产品这三项都不合格，则三项全部合格的建筑防水卷材产品有多少种?_____
A: 37
B: 36
C: 35
D: 34
参考答案: D
本题解释:正确答案是D考点容斥原理问题解析本题注意按照不合格得到三个类，进行容斥原理分析。分别设三项全部合格、仅一项不合格的产品有A、B种，根据题意可得B+7+1=52-A，3×1+2×7+1×B=8+10+9，解得A=34，B=10。故正确答案为D。公式：三集合容斥原理中，将只符合一个条件、只符合两个条件和三个条件都符合的分别看做三个整体，以A、B、C表示三个集合，以X、Y、Z分别表示只符合一个条件、只符合两个条件和三个条件都满足的部分，则有A+B+C=X+2Y+3Z及A∪B∪C=X+Y+Z成立。标签整体考虑公式应用

4、单选题  打印一份稿件，小张5小时可以打完这份稿件的1/3，小李3小时可以打完这份稿件的1/4，如果两人合打多少小时可以完成?_____
A: 6
B: 20/3
C: 7
D: 22/3
参考答案: B
本题解释:正确答案是B考点工程问题解析设总的稿件为60张，由题意，小张每小时打印1/15，小李每小时打印1/12，则小张、小李每小时分别能打印4张、5张。如果两个人合打，每小时打印9张，则打印完这份稿件需要60÷9=20/3(小时)，故正确答案为B。标签赋值思想

5、单选题  某城市居民用水价格为：每户每月不超过5吨的部分按4元/吨收取，超过5吨不超过10吨的部分按6元/吨收取，超过10吨的部分按8元/吨收取。某户居民两个月共交水费108元，则该户居民这两个月用水总量最多为多少吨?_____
A: 21
B: 24
C: 17.25
D: 21.33
参考答案: A
本题解释:正确答案是A考点分段计算问题解析在花费相同的情况下，要使两个月用水量最多，须使水价相对较便宜阶段的用水量最大，即两个月的“不超过5吨”和“5吨到10吨”部分的水量尽量多，通过计算2×(4×5+6×5)=100元，剩余180-100=8元，由于超出10吨的部分按8元/吨收取，故用水量为2×10+1=21吨。故正确答案为A。