1、单选题  一个半径为r的圆用一些半径为r/2的圆去覆盖，至少要用几个小圆才能将大圆完全盖住?_____
A: 5个
B: 6个
C: 7个
D: 8个
参考答案: C
本题解释:正确答案是C考点几何问题解析已知大圆半径为r，小圆半径为r/2，则4个小圆的面积恰好等于一个大圆的面积。为保证小圆尽可能的覆盖大圆，当4个小圆不重叠时，所覆盖大圆部分的面积必小于大圆自身面积，若用5个小圆覆盖大圆，因为小圆的直径等于大圆的半径，所以当5个小圆不重叠时，无法覆盖住大圆的圆周，而6个小圆则恰好盖住大圆圆周，此时中间空白处再加上1个小圆，可将大圆完全覆盖，所以共需要7个小圆，如下图所示。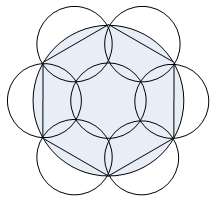

2、单选题  8个甲级队应邀参加比赛，先平均分成两组，分别进行单循环赛，每组决出前两名，再由每组的第一名，另一组的第二名进行淘汰赛，获胜者角逐冠、亚军，败者角逐第3、4名，整个赛程的比赛场数是_____。
A: 16
B: 15
C: 1
D: 13
参考答案: A
本题解释:正确答案是A考点排列组合问题解析

3、单选题  71/79，129/137，23/31，246/254中最大的是_____。
A: 71/79
B: 129/137
C: 23/31
D: 246/254
参考答案: D
本题解释:正确答案是D考点计算问题解析题干中四个分数可分别变形为1-8/79、1-8/137、1-8/31、1-8/254，易知1-8/254>1-8/137>1-8/79>1-8/31，于是题干中四个分数最大的是246/254。故正确答案为D。

4、单选题  某高校对一些学生进行问卷调查。在接受调查的学生中，准备参加注册会计师考试的有63人，准备参加英语六级考试的有89人，准备参加计算机考试的有47人，三种考试都准备参加的有24人，准备选择两种考试都参加的有46人，不参加其中任何一种考试的都15人。问接受调查的学生共有多少人?_____
A: 120
B: 144
C: 177
D: 192
参考答案: A
本题解释:正确答案是A考点容斥原理问题解析假设只参加一种考试的有X人，则可知：X+46×2+24×3=63+89+47，可知X=35，因此接受调查的学生共有35+46+24+15=120人。故正确答案为A。注：将只符合一个条件、只符合两个条件和三个条件都符合的分别看作三个整体，以A、B、C表示三个集合，以X、Y、Z分别表示只符合一个条件、只符合两个条件和三个条件都满足的部分，则有A+B+C=X+2Y+3Z及A∪B∪C=X+Y+Z成立。

5、单选题 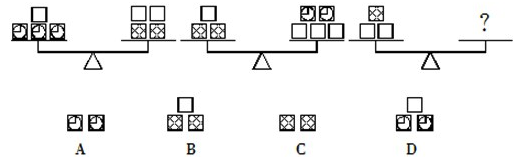 A: A
B: B
C: C
D: D
参考答案: A
本题解释:正确答案是A考点趣味数学问题解析设空白图案为a，交叉图案为b，钟表图案为c，故可得如下：a+c×3=a×2+b×2，a+b×2=c×2+a×3，解得c=3a，b=4a;则可得a×2+b=6a=2c，故正确答案为A。