1、单选题 师徒两人合作完成一项工程,由于配合得好,师傅的工作效率比单独做时要提高 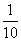 A: 30
A: 30
B: 33
C: 36
D: 42
参考答案: B
本题解释:参考答案:B
题目详解:根据题意,可知:两人合作6天完成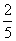
2、单选题 一件工程,甲单独完成需2天,乙单独完成需要4天,如果甲干完一天后,剩下的工程由乙单独完成,则干完此项工程共需_____。
A: 3天
B: 4天
C: 5天
D: 6天
参考答案: A
本题解释:参考答案:A
题目详解:解法一:设工作总量为“1”,那么:甲每天做的工作量为:
3、单选题 原计划用24个工人挖一定数量的土,按计划工作5天后,因为调走6人,于是剩下的工人每天比原计划多挖1方土才能如期完成任务,则原计划每人每天挖土_____。
A: 6方
B: 5方
C: 4方
D: 3方
参考答案: D
本题解释:参考答案
题目详解:解法一:调走6人后,还剩下18人,每人每天增1方,则一天共增加18方,为这6个人的工作量,所以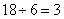
4、单选题 甲、乙、丙三个工程队的效率比为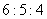 A: 6
A: 6
B: 7
C: 8
D: 9
参考答案: A
本题解释:参考答案:A
题目详解:解法一:由题意可设甲、乙、丙每日工作量分别为6、5、4,丙队参与A工程x天,那么参加B工程(16-x)天,根据A、B工作量相同可列方程: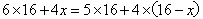
5、单选题 (2009吉林,第7题)甲、乙一起工作来完成一项工程,如果甲单独完成需要30天,乙单独完成需要24天,现在甲、乙一起合作来完成这项工程,但是乙中途被调走若干天,去做另一项任务,最后完成这项工程用了20天,问乙中途被调走_____天。
A: 8
B: 3
C: 10
D: 12
参考答案: D
本题解释:参考答案
题目详解:解法一:假设工程总量为“120”(30与24的最小公倍数),由题意易知:甲的工作效率为: