1、单选题  如图，甲、乙、丙、丁四个长方形拼成正方形EFGH，中间阴影为正方形。已知，甲、乙、丙、丁四个长方形面积的和是32cm2，四边形ABCD的面积是20cm2。问甲、乙、丙、丁四个长方形周长的总和是_____。 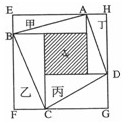A: 32cm
B: 56cm
C: 48cm
D: 68cm
参考答案: C
本题解释:正确答案是C考点几何问题解析根据已知，四边形ABCD的面积为甲、乙、丙、丁四个长方形面积的一半加上阴影部分小正方形的面积，所以小正方形的面积为20-32×1/2=4，正方形EFGH的面积为32+4=36，边长为6，甲、乙、丙、丁四个长方形周长的总和为2×(EA+AH+HD+DG+GC+CF+FB+BE)=2×6×4=48，故正确答案为C。

2、单选题  两个相同的瓶子装满酒精溶液，一个瓶子中酒精与水的体积比是3∶1，另一个瓶子中酒精与水的体积比是4∶1，若把两瓶酒精溶液混合，则混合后的酒精和水的体积之比是多少?_____
A: 31∶9
B: 7∶2
C: 31∶40
D: 20∶11
参考答案: A
本题解释:正确答案是A考点其他解析设两个瓶子每个容量为20，第一个瓶子中酒精和水分别为15和5;另一个瓶子中酒精和水分别为16和4，混合后酒精和水体积比为(15+16)：(5+4)=31：9，故正确答案为A。秒杀技混合后酒精与水的比例显然介于3到4之间，只有选型A、B符合，而选项B显然是题目设置的陷阱选项(直接将数字相加)，因此只剩A项，故正确答案为A。标签赋值思想

3、单选题  网管员小刘负责甲、乙、丙三个机房的巡检工作，甲、乙和丙机房分别需要每隔2天、4天和7天巡检一次。3月1日，小刘巡检了3个机房，问他在整个3月有几天不用做机房的巡检工作：_____
A: 12
B: 13
C: 14
D: 15
参考答案: C
本题解释:正确答案是C，解析方法一：根据三集合容斥原理的标准公式：需要工作的天数为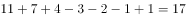

4、单选题  草地上插了若干根旗杆，已知旗杆的高度在1至5米之间，且任意两根旗杆的距离都不超过它们高度差的10倍。如果用一根绳子将所有旗杆都围进去，在不知旗杆数量和位置的情况下，最少需要准备多少米长的绳子?_____
A: 40
B: 100
C: 60
D: 80
参考答案: D
本题解释:正确答案是D考点几何问题解析解析1：

5、单选题  有两个班的小学生要到少年宫参加活动，但只有一辆车接送。第一班的学生坐车从学校出发的同时，第二班学生开始步行。车到途中某处，让第一班学生下车步行，车立刻返回接第二班学生上车并直接开往少年宫，学生步行速度为每小时4公里，载学生时车速每小时40公里，空车每小时50公里，那么，要使两班学生同时到达少年宫，第一班学生步行了全程的几分之几?(学生上下车时间不计)_____。
A: 1/7
B: 1/6
C: 3/4
D: 2/5
参考答案: A
本题解释:正确答案是A考点行程问题解析为了使两班同时到达，必须满足一个条件，即两班行走的距离相等，坐车的距离也相等。设二班步行的距离为x，一班坐车的距离为y，则一班行走的距离也为x，二班的坐车距离为y。由线段图可知：二班步行时间=(一班坐车时间+空车跑回接二班的时间)，所以得x/4=y/40+(y-x)/50，解得x/y=1/6，所以x占全程的1/7，故正确答案为A。