1、单选题  有一项工程含A、B、C、D、E、F六道工序，每道工序分别需要2天、3天、2天、5天、4天、1天时间完成，其中，(1)工序A、B第一天就可以同时动工;(2)工序C必须在工序A、B都完成后才可以动工;(3)工序D必须在工序C完成后才可以动工;(4)工序E必须在工序C完成后才可以动工;(5)工序F必须在工序D、E都完成后才可以动工。那么，完成这项工程至少需要多少天?_____
A: 10
B: 11
C: 12
D: 13
参考答案: B
本题解释:参考答案:B
题目详解:A、B第一天同时动工，A、B都完成需3天。C第四天动工，完成需2天。D、E第六天同时动工，D、E都完成需要5天。F第十一天动工，完成需1天，故完成工程至少需要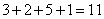

2、单选题  有a、b、c三个数，已知a×b=24，a×c=36，b×c=54，求a+b+c=_____。
A: 23
B: 21
C: 19
D: 17
参考答案: C
本题解释:正确答案是C考点计算问题解析根据a×c=36，b×c=54可得
A:b=2：3，又a×b=24，可知a=4，b=6，再根据b×c=54，可得c=9，因此a+b+c=19，故正确答案为C。

3、单选题  小明参加福建省2004年“奋进杯”中学数学竞赛获了奖(前10名)。爸爸问他：“这次数学竞赛你得了多少分?获得了第几名?”小明说：“我的数学得分是整数，分数和我得的名次与我的年龄相乘的积为2910。”从上面的对话中可以推出小明得了第几名?_____
A: 第一名
B: 第二名
C: 第三名
D: 第四名
参考答案: B
本题解释:正确答案是B考点多位数问题解析先把2910分解成几个质因数相乘，2910=2×3×5×97，由题意知，小明是中学生，且小明获得了前10名，则97是小明的得分，3×5=15是小明的年龄，2是小明获得的名次，故正确答案为B。注：自然数中任何一个合数都可以表示成若干个质因数乘积的形式，如果不考虑因数的顺序，那么这个表示形式是唯一的。

4、单选题  某人以96元的价格出售了两枚古铜币，一枚挣了20%，一枚亏了20%。问：此人盈利或亏损的情况如何？_____
A: 挣了8元      
B: 亏了8元      
C: 持平      
D: 亏了40元
参考答案: B
本题解释: 【解析】B。96×2-[96÷（1+20%）+96÷（1-20%）]=192-200=-8，亏了8元。

5、单选题  某单位招录了10名新员工，按其应聘成绩排名1到10，并用10个连续的四位自然数依次作为他们的工号，凑巧的是每个人的工号都能被他们的成绩排名整除，问排名第三的员工工号所有数字之和是多少_____。
A: 12
B: 9
C: 15
D:来源:91考试网 www.91exAm.org 18
参考答案: A
本题解释:正确答案是A考点多位数问题解析假设10个工号依次为N+1、N+2、……、N+10，由题意，N+A能够被A整除(A为1、2、……、10)，则N能够被A整除。于是N能够被1、2、……、10整除，因此N至少为1、2、……、10的最小公倍数，则在四位数上N最小为2520，可知此时第三位工号为2523，其数字和为12。故正确答案为A。秒杀技由题意第三位的工号加上6后为第九位的工号，因此能被9整除，也即第三位的工号数字之和加上6后能够被9整除，在四个选项中仅A符合。标签数字特性