1、单选题  市民广场中有两块草坪，其中一块草坪是正方形，面积为400平方米，另一块草坪是圆形，其直径比正方形边长长10%，圆形草坪的面积是多少平方米？_____
A: 410            
B: 400            
C: 390          
D: 380
参考答案: D
本题解释: 【解析】正方形的边长是20米，那么圆的半径是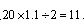

2、单选题  甲、乙两人进行乒乓球比赛，比赛采取三局两胜制，无论哪一方先胜两局则比赛结束。甲每局获胜的概率为2/3，乙每局获胜的概率为1/3。问甲最后取胜的概率是多少?_____A: A
B: B
C: C
D: D
参考答案: A

3、单选题  在一个老年活动中心，会下象棋的有59人，会下围棋的有48人，两种棋都不会下的有12人，两种棋都会下的有30人，问这个俱乐部一共有多少人?_____
A: 89人
B: 107人
C: 129人
D: 137人
参考答案: A
本题解释:正确答案是A考点容斥原理问题解析根据两集合容斥原理，设该俱乐部总人数为a，则59+48-30=a-12，解得a=89(人)，故正确答案为A。注：两集合容斥原理推论公式：满足条件1的个数+满足条件2的个数-都满足的个数=总数-都不满足的个数。

4、单选题  有一根长240米的绳子，从某一端开始每隔4米作一个记号，每隔6米也作一个记号。然后将标有记号的地方剪断，则绳子共剪成_____段。
A: 40
B: 60
C: 80
D: 81
参考答案: C
本题解释:【答案】C。解析：容斥原理，每隔4米作一个记号，则作记号数为240÷4－1＝59；每隔6米作一个记号，则作记号数为240÷6－1＝39；其中每隔12米的记号重复被作两次，类似的记号数为240÷12－1＝19。因此做记号总数为59＋39－19＝79，即绳子被剪成80段。故正确答案为C。两集合容斥原理公式：|A∪B|＝|A|＋|B|－|A∩B|

5、单选题  甲、乙、丙三名运动员囊括了全部比赛项目的前三名，他们的总分分别是8、7和17分，甲得了一个第一名，已知各个比赛项目分数相同，且第一名的得分不低于二、三名得分的和，那么比赛共有多少个项目?_____
A: 3
B: 4
C: 5
D: 6
参考答案: B
本题解释:【答案解析】全部比赛前三名的总分为8+7+17=32分，每个项目前三名的分数和至少是3+2+1=6分，所以每个项目前三名的分数和应该是32的大于6的约数，只能是8、16、32;如果是16或32，因为甲得了一个第一，所以甲的得分应大于8，不合题意，所以每个项目前三名的分数和是8分，共有项目32÷8=4个。