1、单选题  从1，2，3，……，30这30个数中，取出若干个数，使其中任意两个数的积都不能被4整除。问最多可取几个数?_____
A: 14个
B: 15个
C: 16个
D: 17个
参考答案: C
本题解释:正确答案是C考点多位数问题解析任意两个数之积不能被4整除，那么所取数中最多只能有一个偶数，且该偶数不能为4的倍数;共有15个奇数，所以最多可以取15+1=16个数。故正确答案为C。标签数字特性

2、单选题  某办公室共有7个科员，2个副主任，现安排1个副主任带4个科员作出考察，不同的安排方案共有_____。
A: 70种
B: 210种
C: 212种
D: 420种
参考答案: A
本题解释:正确答案是A考点排列组合问题解析

3、单选题 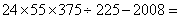 A: 168
B: 172
C: 184
D: 192
参考答案: D
本题解释:参考答案
题目详解:<暂无>考查点:数量关系>数学运算>计算问题之数的性质>数字问题>数字的拆分

4、单选题  某人上午8点要上班，可是发现家里的闹钟停在了6点10分，他上足发条但忘了对表就急急忙忙的上班去了，到公司一看还提前了10分钟。中午12点下班后，回到家一看，闹钟才11点整，假定此人上班、下班在路上用的时间相同，那么他家的闹钟停了多少分钟?_____
A: 100
B: 90
C: 80
D: 70
参考答案: C
本题解释:【解析】C。由题意知：6时10分+闹钟停的时间=7时50分;11时+闹钟停的时间=12时+下班后路上走的时间，所以闹钟停的时间+上班时间=7时50分-6时10分=100分钟，闹钟停的时间上班时间=12时-11时=60分，故闹钟停的时间为（100+60）÷2=80分钟。

5、单选题  从甲、乙两车站同时相对开出第一辆公共汽车，此后两站每隔8分钟再开出一辆，以此类推。已知每辆车的车速相同且都是匀速的，每辆车到达对方站都需要45分钟。现有一乘客坐甲站开出的第一辆车去乙站，问他在路上会遇到几辆从乙站开出的公共汽车。_____。
A: 4辆
B: 5辆
C: 6辆
D: 7辆
参考答案: C
本题解释:正确答案是C考点计数模型问题解析乘客从甲站出发，45分钟内共有6个时间段乙站会发车，出发时间分别为0、8、16、24、32、40分钟，故乘客在路会遇到6辆车，正确答案为C。