1、单选题  某班对50名学生进行体检，有20人近视，12人超重，4人既近视又超重。该班有多少人既不近视又不超重?_____
A: 22人
B: 24人
C: 26人
D: 28人
参考答案: A
本题解释:正确答案是A考点容斥原理问题解析根据两集合容斥原理可知，近视和超重的人士共有20+12-4=28人，可得既不近视也不超重的人数为50-28=22人。故正确答案为A。标签两集合容斥原理公式

2、单选题  已知甲、乙两人共有260本书，其中甲的书有13%是专业书，乙的书有12.5%是专业书，问甲有多少本非专业书?_____
A: 75
B: 87
C: 174
D: 67
参考答案: B
本题解释:正确答案是B考点和差倍比问题解析由“甲的书有13%是专业书”可知，甲的专业书=甲的书×13%，所以甲的书是100的倍数，甲的非专业书是87的倍数，排除A、D。由“乙的书有12.5%是专业书”可知，乙的专业书=乙的书×12.5%=乙的书×1/8，所以乙的书是8的倍数。结合选项，若甲的专业书为174本，则甲有200本书，那么乙的书有60本，不是8的倍数，排除C，故正确答案为B。标签数字特性

3、单选题  有4支队伍进行4项比赛，每项比赛的第一、第二、第三、第四名分别得到5、3、2、1分。每队的4项比赛得分之和算作总分，如果已知各队的总分不相同，并且A队获得了三项比赛的第一名，问总分最少的队伍最多得多少分?_____
A: 7
B: 8
C: 9
D: 10
参考答案: B
本题解释:正确答案是B考点抽屉原理问题解析设四个队分别为A、B、C、D，得分A>B>C>D。已知A得到3个第一，,要使D得到最多的分，那么A的得分要尽可能低，则第四项比赛得分为1，A总得分为5×3+1=16分;四项比赛总分为(5+3+2+1)×4=44，故剩余分数44-16=28;28÷3=9余1，则B最低得分为9+1=10，此时C、D同分，都为9分，不符合题意;则B最低得分为11，此时C得9分，D得8分，符合要求，得分情况如下：
A:5、5、5、1;
B:3、3、3、2;
C:1、1、2、5;
D:2、2、1、3。故正确答案为B。

4、单选题  甲、乙两人站着匀速上升的自动扶梯从底部向顶部行走，甲每分钟走扶梯的级数是乙的2倍;当甲走了36级到边顶部，而乙则走了24级到顶部。那么，自动扶梯有多少级露在外面?_____
A: 68
B: 56
C: 72
D: 85
参考答案: C
本题解释:正确答案是C考点行程问题解析甲、乙走到顶部时间之比为36/2:24=3:4，则扶梯运送两人的距离之比也为3:4，分别假定为3x、4x。假设扶梯总长为N，则可得：N=36+3x，N=24+4x，解得N=72，x=12。故正确答案为C。

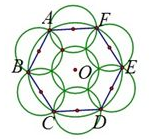
5、单选题  为了浇灌一个半径为10米的花坛，园艺师要在花坛里布置若干个旋转喷头，但库房里只有浇灌半径为5米的喷头，问花坛里至少要布置几个这样的喷头才能保证每个角落都能浇灌到?_____
A: 4
B: 7
C: 6
D: 9
参考答案: B
本题解释:正确答案是B考点几何问题解析注意到对一个圆而言，圆弧是最外层，因此在浇灌时首先要保证整个圆弧能够被覆盖到。一个小圆只能覆盖一段圆弧，由于每个小圆的直径为10，也即一个小圆覆盖圆弧对应的弦最长为10，而大圆的半径为10，所以每个小圆至多盖住圆心角为60°所对应的弧长。因此想盖住整个圆圈，至少需要六个小圆，并且当且仅当这六个小圆以大圆的内接正六边形各边中点为圆心进行覆盖。此时大圆的圆心处尚未被覆盖，还需要一个小圆才能完成覆盖。如图所示，故正确答案为B。