1、单选题  完成某项工程，甲单独工作需要18小时，乙需要24小时，丙需要30小时。现按甲、乙、丙的顺序轮班工作，每人工作一小时换班。当工程完工时，乙总共干了多少小时?_____
A: 8小时
B: 7小时44分
C: 7小时
D: 6小时48分
参考答案: B
本题解释:正确答案是B考点工程问题解析解析1：设工程总量为360，则甲乙丙的工作效率分别为20、15、12，三人每小时工作总量为47。由题意可知三人轮班即为循环周期问题，用360除以47商7余数为31，甲乙丙轮班每人7小时后，乙继续工作的工作量为31-20=11。所以最终乙总共干了：7小时+11/15×60分=7小时44分，故正确答案为B。解析2：设工程总量为360，则甲乙丙的工作效率分别为20、15、12，甲每小时比乙多干5，乙每小时比丙多干3，因此乙工作时间必定小于24/3=8小时。观察选项有6小时、7小时和8小时，可选7为参考点，甲乙丙轮班每人工作7小时共完成：(20+15+12)×7=329<360，因此乙工作时间在7小时和8小时之间，故正确答案为B。

2、单选题  下图是由5个相同的小长方形拼成的大长方形，大长方形的周长是88厘米，问大长方形的面积是多少平方厘米?_____ 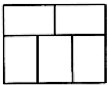A: 472平方厘米
B: 476平方厘米
C: 480平方厘米
D: 484平方厘米
参考答案: C
本题解释:正确答案是C考点几何问题解析通过观察大长方形的上下两边，可见小长方形的长宽比为3：2，则设小长方形的长宽分别为3y、2y，根据题意得，3y×4+2y×5=88，解得y=4，因此大长方形长为：3y×2=24，宽为：3y+2y=20，则大长方形的面积为：24×20=480，故选择C选项。秒杀技由题意给出”5个相同的小长方形”，因此大长方形的面积是小长方形的5倍，由此可知面积应能被5整除，故答案为C。标签数字特性

3、单选题  一个圆能把平面分成两个区域，两个圆可以把平面分成四个区域，问四个圆最多可能把平面分成多少个区域?_____
A: 14
B: 13
C: 16
D: 15
参考答案: A
本题解释:正确答案是A考点几何问题解析

4、单选题  一个班里有30名学生，有12人会跳拉丁舞，有8人会跳肚皮舞，有10人会跳芭蕾舞。问至多有几人会跳两种舞蹈?_____
A: 12人
B: 14人
C: 15人
D: 16人
参考答案: C
本题解释:正确答案是C考点统筹规划问题解析要使会跳两种舞蹈的人最多，则尽量在三种舞蹈之间进行匹配，使得两两匹配的人数之和最多。因此就不能将一种舞蹈只与另一种舞蹈进行全额匹配，例如不能将会跳肚皮舞的8人全部与拉丁舞匹配。实际上，为实现两两匹配的最多，则每组用于匹配的人数应相等或接近。从最少人数出发，会跳肚皮舞的8人，将其划分时要考虑拉丁舞和芭蕾舞人数相差2，故在划分此8人时注意这一点，可将8人划分为5人和3人。其中5人除了会肚皮舞之外，还会拉丁舞;3人会肚皮舞之外还会芭蕾舞。此时拉丁舞与芭蕾舞还各自剩7人、7人，又可以匹配得到7人既会拉丁舞又会芭蕾舞。会跳两种舞的人数至多为15人。故正确答案为C。秒杀技假定拉丁+肚皮、肚皮+芭蕾、芭蕾+拉丁的人数分别为x、y、z，则根据题意可知x+y≤8，x+z≤12，y+z≤10，求取x+y+z的最大值。对于前述三个不等式，先将不等号变为等号尝试求解一下，恰好可得x=5，y=3，z=7，代回验证可知所有条件均满足。因此可知x+y+z的最大值为15。故正确答案为C。标签构造调整

5、单选题  某路公交车单程共有10个车站，从始发站出发时，车上共有乘客20人，之后中间每站新上5人，且车上所有乘客最多做3站下车。问最多会有多少名乘客在终点站下车?_____
A: 20
B: 10
C: 5
D: 15
参考答案: D
本题解释:正确答案是D考点趣味数学问题解析由题意，最初的20人在第4站都要下车;每一站新上的人都在3站后下车，那么只有第7站及以后的人才可能在终点站下车。也就是说最多有第7站、第8站、第9站的新上的人在终点站下车，因此最多有15人在终点站下车，正确答案为D。