1、单选题  共计33个三角形和四边形，有111个角，则四边形的个数为_____。
A: 10 
B: 11 
C: 12 
D: 13
参考答案: C
本题解释: C [解析] 设四边形的个数为x，由题意可得：4x+（33-x）×3=111，解得x=12，即应该有12个四边形。故本题选C。

2、单选题  甲、乙两个厂生产同一种玩具，甲厂生产的玩具数量每天保持不变，乙厂生产的玩具数量每天增加一倍，已知第一天甲、乙两个厂生产的玩具总数是98件，第二天甲、乙两个厂生产的玩具总数是106件。那么乙厂生产的玩具数量第一次超过甲厂生产的玩具数量是在第几天?_____
A: 3
B: 4
C: 5
D: 7
参考答案: C
本题解释:正确答案是C考点不等式分析问题解析

3、单选题  调查发现，男女生各半的一个100人的班，20%患有色盲症，其余正常;如果女生有色盲5人，则正常男生的人数是_____。
A: 15
B: 30
C: 35
D: 40
参考答案: C
本题解释:正确答案是C考点和差倍比问题解析由题可知，色盲人数为100×20%=20(人)，故男生中色盲人数为20-5=15(人)。又知男、女各半，故男生为50人，50-15=35(人)，即为正常男生人数。故正确答案为C。

4、单选题  某校参加数学竞赛的有120名男生，80名女生，参加语文竞赛的有120名女生，80名男生。已知该校总共有260名学生参加了竞赛，其中有75名男生两科都参加了，则只参加数学竞赛而没有参加语文竞赛的女生有_____。
A: 65人
B: 60人
C: 45人
D: 15人
参考答案: D
本题解释:正确答案是D考点容斥原理问题解析参加数学竞赛的有200名学生，参加语文竞赛的也有200名学生，则两科都参加的共有200+200-260=140名学生，因有75名男生两科都参加，则有140-75=65名女生两科都参加，所以只参加数学竞赛的女生有80-65=15名。故正确答案为D。

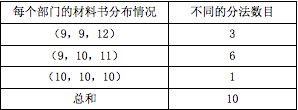
5、单选题  某单位订阅了30份学习材料发放给3个部门，每个部门至少发放9份材料。问一共有多少种不同的发放方法?_____
A: 7
B: 9
C: 10
D: 12
参考答案: C
本题解释:正确答案是C考点排列组合问题解析