1、单选题  用一个平面将一个边长为1的正四面体切分为两个完全相同的部分，则切面的最大面积为_____。A: A
B: B
C: C
D: D
参考答案: B
本题解释:正确答案是B考点几何问题解析

2、单选题  一条路上依次有A、B、C三个站点，加油站M恰好位于A、C的中点，加油站N恰好位于B、C的中点，若想知道M和N两个加油站之间的距离，只需知道哪两点之间的距离?_____
A: B和C
B: C和N
C: A和M
D: A和B
参考答案: D
本题解释:正确答案是D考点几何问题解析画图分析可知，MN=AC/2-BC/2=(AC-BC)/2=AB/2，则只需知道AB的距离，就可知道MN的距离。故正确答案为D。

3、单选题  用直线切割一个有限平面，后一条直线与此前每条直线都要产生新的交点，第1条直线将平面分成2块，第2条直线将平面分成4块。第3条直线将平面分成7块，按此规律将平面分为22块需_____。
A: 如果A、B、P不在同一条直线上，汽车所在位置有3个，可位于A、B两地之间或A、B两地外侧
B: 如果A、B、P不在同一条直线上，汽车的位置有无穷多个
C: 如果A、B、P位于同一条直线上，汽车拉于A、B两地之间或两地外侧
D: 如果A、B、P位于同一条直线上，汽车位于A、B两地外侧，且汽车到A的距离为20千米
参考答案: D
本题解释:正确答案是B考点几何问题解析AB距离为40，AP和BP距离之和为60千米，若A、B、P三点在同一直线上，则P点位于AB外侧10千米处;若A、B、P三点不在同一直线上，则转化为A、B点固定，AP+BP=60即可，有无数种选择。故答案为B。

4、单选题  长为1米的细绳上系有一个小球，从A处放手以后，小球第一次摆到最低点B处共移动了多少米?_____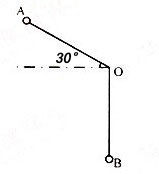A: 1+(1/3)π
B: 1/2+(1/2)π
C: (2/3)π
D: 1+(2/3)π
参考答案: A
本题解释:正确答案是A考点几何问题解析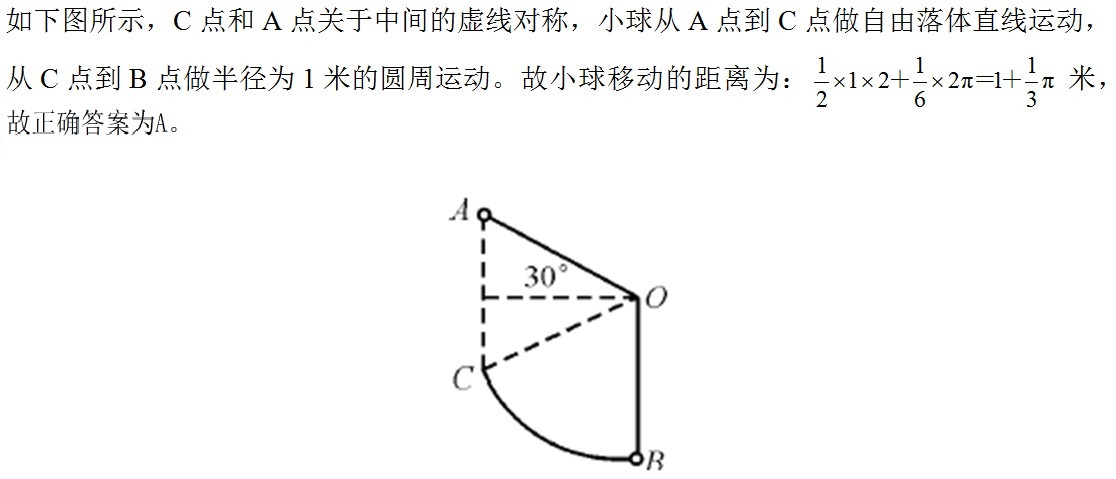

5、单选题  某厂生产一批商标，形状为等边三角形或等腰三角形。已知这批商标边长为2cm或4cm，那么这批商标的周长可能是_____。
A: 6cm12cm
B: 6cm8cm12cm
C: 6cm10cm12cm
D: 6cm8cm10cm12cm
参考答案: C
本题解释:正确答案是C考点几何问题解析三角形的两边之和必须大于第三边，因此三边可能有三种情况：(2，2，2)、(2，4，4)、(4，4，4)，周长为分别为6cm、10cm、12cm，故正确答案为C。