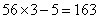1、单选题  某城市居民用水价格为：每户每月不超过5吨的部分按4元/吨收取，超过5吨不超过10吨的部分按6元/吨收取，超过10吨的部分按8元/吨收取。某户居民两个月共交水费108元，则该户居民这两个月用水总量最多为多少吨?_____
A: 21
B: 24
C: 17.25
D: 21.33
参考答案: A
本题解释:正确答案是A考点分段计算问题解析在花费相同的情况下，要使两个月用水量最多，须使水价相对较便宜阶段的用水量最大，即两个月的“不超过5吨”和“5吨到10吨”部分的水量尽量多，通过计算2×(4×5+6×5)=100元，剩余180-100=8元，由于超出10吨的部分按8元/吨收取，故用水量为2×10+1=21吨。故正确答案为A。

2、单选题  某次数学竞赛设一、二等奖。已知(1)甲、乙两校获奖的人数比为 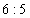A: 20
B: 30
C: 50
D: 60
参考答案: C
本题解释:参考答案:C
题目详解:已知甲、乙两校获二等奖的人数之比为5:6，那么设甲获二等奖的人数为5份，乙为6份。因为二等奖的人数占两校人数总和的60%，那么甲校获二等奖人数占总数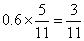

3、单选题  某村有甲乙两个生产小组，总共50人，其中青年人共13人。甲组中青年人与老年人的比例是2：3，乙组中青年人与老年人的比例是1：5，甲组中青年人的人数是_____。
A: 5人
B: 6人
C: 8人
D: 12人
参考答案: C
本题解释:正确答案是C考点和差倍比问题解析解析1：由题意可知，甲组青年人占甲组总人数的2/5，乙组青年人占乙组总人数的1/6，假设甲组青年人人数为x，则乙组青年人人数为13-x，列出方程，可得x÷2/5+(13-x)÷1/6=50，解得x=8，则甲组青年人人数为8人。故正确答案为C。解析2：由题意可知，甲组青年人占甲组总人数的2/5，乙组青年人占乙组总人数的1/6，因此甲组人数比能被5整除，乙组人数比能被6整除。而乙组人数又等于50减去甲组人数，因此乙组人数也能被5整除，满足这个条件的，只有甲组为20人，乙组为30人，甲组中青年人的人数为20×2/5=8。故正确答案为C。标签数字特性

4、单选题  一项任务甲做要半小时完成，乙做要45 分钟完成，两人合作需要多少分钟完成？_____
A: 12 
B: 15 
C: 18 
D: 20
参考答案: C
本题解释:【解析】直接设90的总量，两人每分钟分别是3和2。所以90/（3+2）=18。

5、单选题  一个自然数，被7除余2，被8除余3，被9除余1，1000以内一共有多少个这样的自然数?_____
A: 5
B: 2
C: 3
D: 4
参考答案: B
本题解释:参考答案:B
题目详解:7、8的最小公倍数为56，根据"差同减差，公倍数做周期"可知：所有满足条件的数可表示为56n-5，也就是除以56余5;要让所有56n-5中满足被9除余1：最小数是n=3时：