1、单选题  100个自然数的和是20000，其中奇数的个数比偶数的个数多，那么偶数最多能有多少个?_____
A: 38
B: 40
C: 48
D: 49
参考答案: C
本题解释:参考答案:C
题目详解:依题意：“100个自然数的和是20000”，即和为偶数;又因为奇数的个数为偶数个，奇数的个数比偶数的个数多：所以最多有100÷2-2=48个偶数;所以，选C。考查点:数量关系>数学运算>计算问题之数的性质>奇偶性与质合性问题>奇偶性

2、单选题  某校人数是一个三位数，平均每个班级36人，若将全校人数的百位数与十位数对调，则全校人数比实际少180人，那么全校人数最多可以达到多少人?_____
A: 900
B: 936
C: 972
D: 990
参考答案: C
本题解释:参考答案:C
题目详解:使百位数与十位数对调后，比实际少180人：百位比十位必须大2;根据题意应是九百七十几;又因为这个三位数是36倍数：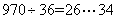

3、单选题  某超市购进一批商品，按照能获得50%的利润的定价，结果只销售了70%，为尽快将余下的商品销售出去，超市决定打折出售，这样所获得的全部利润是原来能获得利润的82%，问余下的商品几折出售？_____
A: 6.5折
B: 7折
C: 7.5折
D: 8折
参考答案: D
本题解释:D。设成本100，定价150，则原来一件利润是50，再设折扣X，共有Y件商品，所以50Y*0.7+（150X-100）0.3Y=50Y*0.82，整理得X=0.8，选D。

4、单选题  某高校对一些学生进行问卷调查。在接受调查的学生中，准备参加注册会计师考试的有63人，准备参加英语六级考试的有89人，准备参加计算机考试的有47人，三种考试都准备参加的有24人，准备选择两种考试都参加的有46人，不参加其中任何一种考试的都15人。问接受调查的学生共有多少人?_____
A: 120
B: 144
C: 177
D: 192
参考答案: A
本题解释:正确答案是A考点容斥原理问题解析假设只参加一种考试的有X人，则可知：X+46×2+24×3=63+89+47，可知X=35，因此接受调查的学生共有35+46+24+15=120人。故正确答案为A。注：将只符合一个条件、只符合两个条件和三个条件都符合的分别看作三个整体，以A、B、C表示三个集合，以X、Y、Z分别表示只符合一个条件、只符合两个条件和三个条件都满足的部分，则有A+B+C=X+2Y+3Z及A∪B∪C=X+Y+Z成立。

5、单选题  某机关20人参加百分制的普法考试，及格线为60分，20人的平均成绩为88分，及格率为95%。所有人得分均为整数，且彼此得分不同。问成绩排名第十的人最低考了多少分?_____
A: 88
B: 89
C: 90
D: 91
参考答案: B
本题解释:正确答案是B考点多位数问题解析要使第十名成绩尽可能的低，那么其他人应该尽可能的高，那么前九名应该分别为100、99、98、97、96、95、94、93、92分，而最后一名未及格，最多59分，此十人成绩之和为923，还剩837分。现要把这837分分给其余10个人，而在这10个人成绩排名第十的人成绩最高，要使其得分最低，则这10人的成绩应尽可能接近。易知此10人平均分为83.7，据此可构造79、80、81、82、83、84、85、86、88、89，因此成绩排名第十的人最低考了89分。故正确答案为B。