微信搜索关注"91考试网"公众号,领30元,获取公务员、事业编、教师等考试资料40G!
1、某公司三名销售人员2011年的销售业绩如下:甲的销售额是乙和丙销售额的1.5倍,甲和乙的销售是丙的销售额的5倍,已知乙的销售额是56万元,问甲的销售额是_____。
A: 140万元B: 144万元C: 98万元D: 112万元
参考答案: B 本题解释:正确答案是B考点和差倍比问题解析由题意,甲=1.5(乙+丙),甲+乙=5丙,将乙=56代入,可得甲=144,丙=40。故答案为B。秒杀技秒杀一:由甲的销售额是乙丙之和的1.5倍,而1.5中含有因子3,因此甲的销售额能被3整除,仅B符合。秒杀二:甲和乙的销售额之和是丙销售额的5倍,因此甲乙销售额之和能够被5整除,其尾数为0或5,在四个选项中仅B符合这一要求。
2、甲、乙、丙、丁四个队共同植树造林,甲队造林的亩数是另外三个队造林总亩数的1/4,乙队造林的亩数是另外三个队造林总亩数的1/3,丙队造林的亩数是另外三个队造林总亩数的一半,已知丁队共造林3900亩,问甲队共造林多少亩?_____
A: 9000B: 3600C: 6000D: 4500
参考答案: B 本题解释:正确答案是B考点和差倍比问题解析
3、某公司去年有员工830人,今年男员工人数比去年减少6%,女员工人数比去年增加5%,员工总数比去年增加3人,问今年男员工有多少人?_____
A: 329B: 350C: 371D: 504
参考答案: A 本题解释:正确答案是A考点和差倍比问题解析设去年男员工X人,女员工Y人,由题意知:X+Y=830,5%Y-6%X=3,解得X=350。今年男员工减少了,所以人数小于350,只有A符合条件,故正确答案为A。秒杀技由题知,今年男员工数是去年的94%,所以今年男员工数可被94%整除,根据选项,只有A符合。故正确答案为A。标签数字特性
4、某人银行账户今年底余额减去1500元后,正好比去年底余额减少了25%,去年底余额比前年余额的120%少2000元,则此人银行账户今年底余额一定比前年底余额_____。
A: 多1000元B: 少1000元C: 多10%D: 少10%
参考答案: D 本题解释:正确答案是D考点和差倍比问题解析设前年底余额为m元,则去年为(1.2m-2000)元,今年为[0.75×(1.2m-2000)+1500]元,化简得今年为0.9m元,即今年底余额比前年底减少10%,故正确答案为D。标签逆向考虑
5、某市气象局观测发现,今年第一、二季度本市降水量分别比去年同期增加了11%和9%,而两个季度降水量的绝对增量刚好相同。那么今年上半年该市降水量同比增长多少?_____
A: 9.5%B: 10%C: 9.9%D: 10.5%
参考答案: C 本题解释:正确答案是C考点和差倍比问题解析解析1:设绝对增长量是X,则今年上半年的增长量是2X,去年的降水量是X/11%+X/9%,同比增长=2X/(X/11%+X/9%)=9.9%,故正确答案为C。解析2: 标签十字交叉法
标签十字交叉法
6、某高校2006年度毕业学生7650名,比上年度增长2%,其中本科生毕业数量比上年度减少2%,而研究生毕业数量比上年度增加10%,那么,这所高校今年毕业的本科生有_____。
A: 3920人B: 4410人C: 4900人D: 5490人
参考答案: C 本题解释:正确答案是C考点和差倍比问题解析假设去年研究生毕业数为A,本科生毕业数为B,那么今年研究生毕业数为1.1A,本科生毕业数为0.98B。由题意知:A+B=7650÷(1+2%),1.1A+0.98B=7650,解得B=5000人。则今年本科生毕业数量为5000×0.98=4900人,故正确答案为C。秒杀技由“本科生比上年度减少2%”可知“今年本科生数=98%×去年本科生数”(注意98%是百分数,本质上也是个分数),所以今年本科生应能够被49整除。由“研究生毕业数量比上年增加10%”知“今年研究生数=110%×去年研究生数”,所以今年研究生数应能够被11整除,据此两条得出正确答案为C。
7、某公司甲、乙两个营业部共有50人,其中32人为男性。已知甲营业部的男女比例为5:3,乙营业部的男女比例为2:1,问甲营业部有多少名女职员?_____
A: 18B: 16C: 12D: 9
参考答案: C 本题解释:正确答案是C考点和差倍比问题解析设甲营业部有3X名女职员,乙营业部有Y名女职员,则有5X+2Y=32;32+3X+Y=50,解得X=4,Y=6,故甲营业部有3×4=12名女职员,故正确答案为C。秒杀技有题意可知,两个营业部共有50-32=18名女职员,排除A。根据“乙营业部的男女比例为2:1”可知,乙营业部的男职员为偶数,由于男职员的总人数为偶数,则甲营业部的男职员人数同样为偶数。根据“已知甲营业部的男女比例为5:3”,甲营业部的女职员人数能同时被2和3整除,排除B、D,故正确答案为C。
8、某汽车厂离生产甲、乙、丙三种车型,其中乙型产量的3倍与丙型产量的6倍之和等于甲型产量的4倍,甲型产量与乙型的2倍之和等于丙型产量的7倍。则甲、乙、丙三型产量之比为_____。
A: 5:4:3B: 4:3:2C: 4:2:1D: 3:2:1
参考答案: D 本题解释:正确答案是D考点和差倍比问题解析设甲的产量为x,乙的产量为y,丙的产量为z。则可得如下:3y+6z=4x,x+2y=7z,两式相加可得3x+z=5y,直接带入选项,只有D符合,故正确答案为D。秒杀技得到3y+6z=4x后,观察该式,可知x应为3的倍数,只有D符合。标签直接代入
9、有一食品店某天购进了6箱食品,分别装着饼干和面包,重量分别为8、9、16、20、22、27千克。该店当天只卖出1箱面包,在剩下的5箱中饼干的重量是面包的两倍,则当天食品店购进了_____千克面包。
A: 44B: 45C: 50D: 52
参考答案: D 本题解释:正确答案是D考点和差倍比问题解析由剩下的饼干重量是面包的两倍可知,剩下5箱的总重量一定能被3整除;6箱的总重量是8+9+16+20+22+27=102千克,也能被3整除,因此卖掉的一箱面包的重量也能被3整除,只能是9千克或27千克。若卖掉的一箱面包的重量是9千克,则剩下的面包重(102-9)÷3=31千克,剩余的各箱重量无法组合得到31。所以卖出的面包重27千克,剩余面包重(102-27)÷3=25千克。因此共购进了27+25=52千克面包,故正确答案为D。
10、某小区物业征集业主意见,计划从100户业主中抽取有20户进行调查。100户业主中有b户主年龄超过60岁,a户户主年龄不满35岁,户主年龄在36岁到59岁的有25户。为了使意见更具代表性,物业采取分层抽样的方法,从b户中抽取了4户,则a的值可能是_____。
A: 55B: 66C: 44D: 50
参考答案: A 本题解释:正确答案是A考点和差倍比问题解析100户中抽取20户,可知抽取比例为5:1,根据题意,4:b=20:100,a+b=75,解得a=55。故答案为A。
11、某班男生比女生人数多80%,一次考试后,全班平均成级为75分,而女生的平均分比男生的平均分高20%,则此班女生的平均分是_____。
A: 84分B: 85分C: 86分D: 87分
参考答案: A 本题解释:正确答案是A考点和差倍比问题解析解析1:设男生的平均分为x,则女生的平均分是1.2x。由题意得男、女人数之比为1.8:1,由十字交叉法得(1.2x-75):(75-x)=1.8:1,解得x=70分。则女生的平均分为1.2×70=84分,故正确答案为A。解析2:设男生的平均分为z,女生人数为y。则女生的平均分是1.2z,男生的人数是1.8y。由题意得:1.8zy+1.2zy=75×2.8y,解得z=70分。因此女生的平均分是1.2×70=84分,故正确答案为A。秒杀技由“女生的平均分比男生的平均分高20%”知女生的平均分一定能被12整除,只有A选项符合条件,故正确答案为A。
12、甲乙两个乡村阅览室,甲阅览室科技类书籍数量的1/5相当于乙阅览室该类书籍的1/4,甲阅览室文化类书籍数量的2/3相当于乙阅览室该类书籍的1/6,甲阅览室科技类和文化类书籍的总量比乙阅览室两类书籍的总量多1000本,甲阅览室科技类书籍和文化类书籍的比例为20:1,问甲阅览室有多少本科技类书籍?_____
A: 15000B: 16000C: 18000D: 20000
参考答案: D 本题解释:正确答案是D考点和差倍比问题解析假设甲阅览室科技类书籍有20a本,文化类书籍有a本,则乙阅览室科技类书籍有16a本,文化类书籍有4a本,由题意可得(20a+a)-(16a+4a)=1000,解得a=1000,则甲阅览室有科技类书籍20000本。故正确答案为D。
13、两个派出所某月内共受理案件160起,其中甲派出所受理的案件中有17%是刑事案件,乙派出所受理的案件中有20%是刑事案件,问乙派出所在这个月中共受理多少起非刑事案件?_____
A: 48B: 60C: 72D: 96
参考答案: A 本题解释:正确答案是A考点和差倍比问题解析已知甲派出所受理案件的17%为刑事案件,则甲受理案件数必为100的倍数,才能保证刑事案件数为整数。根据题意,甲派出所受理案件只能为100件,故乙受理案件为60件,可得乙受理非刑事案件数为60×(1-20%)=48件,故正确答案为A。标签数字特性
14、果园里有梨树、桃树、核桃树共526棵,梨树比桃树的2倍多24棵,核桃树比桃树少18棵。求桃树有多少棵?_____
A: 105B: 115C: 125D: 130
参考答案: D 本题解释:参考答案 题目详解:解法一:设桃树有
题目详解:解法一:设桃树有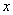 棵,那么梨树有
棵,那么梨树有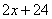 棵,核桃树有
棵,核桃树有 棵,因此
棵,因此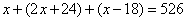 解得,
解得,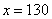 。所以,选D。解法二:“梨树比桃树的2倍多24棵”,如果梨树少24棵,则刚好是桃树的2倍。“核桃树比桃树少18棵”,如果核桃树多18棵,那么刚好与桃树相同。则有:桃树的数目是:
。所以,选D。解法二:“梨树比桃树的2倍多24棵”,如果梨树少24棵,则刚好是桃树的2倍。“核桃树比桃树少18棵”,如果核桃树多18棵,那么刚好与桃树相同。则有:桃树的数目是: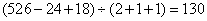 (棵)梨树的数目是:
(棵)梨树的数目是: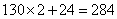 (棵)核桃树的数目是:
(棵)核桃树的数目是: (棵)考查点:数量关系>数学运算>和差倍比问题>和差倍问题
(棵)考查点:数量关系>数学运算>和差倍比问题>和差倍问题
15、有3根钢丝,第一根的长度是第二根的  ,是第三根的
,是第三根的  ,第二根比第三根长了384毫米,现在要把这三段钢丝截成尽可能长且相等的小段,那么这三根钢丝一共可以截成多少小段?_____
,第二根比第三根长了384毫米,现在要把这三段钢丝截成尽可能长且相等的小段,那么这三根钢丝一共可以截成多少小段?_____
A: 10B: 11C: 12D: 15
参考答案: C 本题解释:参考答案:C题目详解:根据题意,可知:第一根:第二根=3:5,第一根:第三根=3:4,所以,第二根:第三根=5:4;所以第二根长384÷(5-4)×5=1920毫米,第一根长1920÷5×3=1152毫米,第三根长1920÷5×4=1536毫米;截成的小段长为三根钢丝长度的最大公约数,(1152,1920,1536)=384毫米,所以这三根钢丝截成了(1152+1920+1536)÷384=12根。因此,选C。考查点:数量关系>数学运算>和差倍比问题>比例问题
16、某次数学竞赛设一、二等奖。已知(1)甲、乙两校获奖的人数比为 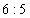 。(2)甲、乙两校获二等奖的人数总和占两校获奖人数总和的
。(2)甲、乙两校获二等奖的人数总和占两校获奖人数总和的 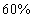 。(3)甲、乙两校获二等奖的人数之比为
。(3)甲、乙两校获二等奖的人数之比为 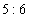 。问甲校获二等奖的人数占该校获奖总人数的百分数是几?_____
。问甲校获二等奖的人数占该校获奖总人数的百分数是几?_____
A: 20B: 30C: 50D: 60
参考答案: C 本题解释:参考答案:C题目详解:已知甲、乙两校获二等奖的人数之比为5:6,那么设甲获二等奖的人数为5份,乙为6份。因为二等奖的人数占两校人数总和的60%,那么甲校获二等奖人数占总数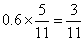 又因为甲、乙两学校获奖人数比为6:5,所以设总人数为11份,甲得奖的占其中6份可知甲校获二等奖者占该校获奖总人数的
又因为甲、乙两学校获奖人数比为6:5,所以设总人数为11份,甲得奖的占其中6份可知甲校获二等奖者占该校获奖总人数的 。所以,选C。考查点:数量关系>数学运算>和差倍比问题>比例问题
。所以,选C。考查点:数量关系>数学运算>和差倍比问题>比例问题
17、某个五位数加上20万并且3倍以后,其结果正好与该五位数的右端增加一个数字2的得数相等,这个五位数是_____。
A: 85714B: 87431C: 90245D: 93142
参考答案: A 本题解释:参考答案:A题目详解:解法一:设该数是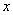 ,则右端增加一个数字2后该数变为
,则右端增加一个数字2后该数变为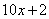 。依题意有:
。依题意有: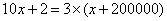 解得,
解得,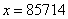 。所以,选A。解法二:使用尾数法。右端增加一个2,则这个数的尾数是2,不管加上多少万都是需要乘以3的,所以只有原来的数尾数为4乘以3才能保证得数的尾数为2。(该解析由用户“阿吉格”于2010-05-2617:24:32贡献,感谢感谢!)考查点:数量关系>数学运算>和差倍比问题>和差倍问题
。所以,选A。解法二:使用尾数法。右端增加一个2,则这个数的尾数是2,不管加上多少万都是需要乘以3的,所以只有原来的数尾数为4乘以3才能保证得数的尾数为2。(该解析由用户“阿吉格”于2010-05-2617:24:32贡献,感谢感谢!)考查点:数量关系>数学运算>和差倍比问题>和差倍问题
18、甲乙两个工厂的平均技术人员比例为45%,其中甲厂的人数比乙厂多12.5%,技术人员的人数比乙厂的多25%,非技术人员人数比乙厂多6人。甲乙两厂共有多少人?_____
A: 680B: 840C: 960D: 1020
参考答案: A 本题解释:正确答案是A考点和差倍比问题解析由题干中"甲厂人数比乙厂多12.5%"可知甲、乙两厂总人数之比为9:8,则可假设甲厂总人数有9n,乙厂总人数有8n,甲乙总人数为17n,故总人数一定能被17整除,排除选项B、C;在A和D之间选择,直接代入A选项,则有680=17n,n=40,则甲厂共360人,乙厂共320人,两厂的技术人员总数为680×45%=306人,甲厂技术人员有170人,非技术人员为190人,乙厂有技术人员136人,非技术人员184人,甲乙两厂的非技术人员相差190-184=6人,满足题意,验证成立。故正确答案为A。标签直接代入数字特性
19、甲、乙两个冷藏库共存鸡蛋6250箱,先从甲库运走1100箱后,这时乙库存的鸡蛋比甲库剩下的2倍还多350箱,求甲库比乙库原来少存了鸡蛋多少箱?_____
A: 550B: 650C: 750D: 850
参考答案: D 本题解释:参考答案 题目详解:根据题意,可知:甲库运走l100箱以后,则:两库还剩下:6250-1100=5150箱,甲库还剩下:(5150-350)÷(1+2)=1600箱;那么,则有:甲库原存鸡蛋为:1600+1100=2700箱,乙库原来存鸡蛋为:1600×2+350=3550箱,甲库比乙库少:3550-2700=850箱。考查点:数量关系>数学运算>和差倍比问题>和差倍问题
题目详解:根据题意,可知:甲库运走l100箱以后,则:两库还剩下:6250-1100=5150箱,甲库还剩下:(5150-350)÷(1+2)=1600箱;那么,则有:甲库原存鸡蛋为:1600+1100=2700箱,乙库原来存鸡蛋为:1600×2+350=3550箱,甲库比乙库少:3550-2700=850箱。考查点:数量关系>数学运算>和差倍比问题>和差倍问题
20、有两堆煤共重8.1吨,第一堆用掉2/3,第二堆用掉3/5,把两堆剩下的合在一起,比原来第一堆还少 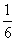 ,原来第一堆煤有多少吨?_____
,原来第一堆煤有多少吨?_____
A: 3.6B: 4.5C: 4D: 4.1
参考答案: A 本题解释:参考答案:A题目详解:解法一:根据题意,可知:用掉后,第一堆煤剩下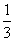 ,第二堆煤剩下
,第二堆煤剩下 ,两堆剩下的合在一起后,占原来第一堆的
,两堆剩下的合在一起后,占原来第一堆的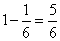 ,这其中有
,这其中有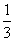 是原来第一堆剩下的,其余的
是原来第一堆剩下的,其余的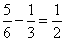 是原来第二堆剩下的,也就是说原来第二堆的
是原来第二堆剩下的,也就是说原来第二堆的 等于第一堆的
等于第一堆的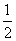 。所以原来第二堆的总数是原来第一堆的
。所以原来第二堆的总数是原来第一堆的 倍。所以原来第一堆煤有:
倍。所以原来第一堆煤有: 吨。所以,选A。解法二:如果第一堆用掉
吨。所以,选A。解法二:如果第一堆用掉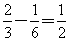 ,这用了的
,这用了的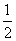 就和第二堆剩下的
就和第二堆剩下的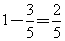 相等,所以,第二堆是第一堆的
相等,所以,第二堆是第一堆的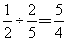 ,所以,第一堆煤有
,所以,第一堆煤有 吨。所以,选A。考查点:数量关系>数学运算>和差倍比问题>比例问题
吨。所以,选A。考查点:数量关系>数学运算>和差倍比问题>比例问题
21、小明买了1支钢笔.所用的钱比所带的总钱数的一半多0.5元;买了1支圆珠笔,所用的钱比买钢笔后余下的钱的一半少0.5元;又买了2.8元的本子,最后剩下0.8元。小明带了多少元钱?_____
A: 14.6B: 16C: 15D: 13.4
参考答案: D 本题解释:参考答案 题目详解:解法一:买本子前剩下
题目详解:解法一:买本子前剩下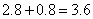 元,根据题意,设总数是
元,根据题意,设总数是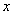 元,则:钢笔花了:
元,则:钢笔花了: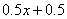 元,圆珠笔花了
元,圆珠笔花了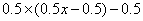 元,那么
元,那么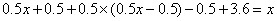 ,解得,
,解得,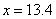 元。所以,选D。解法二:还原问题的思考方法来解答。买圆珠笔后余下
元。所以,选D。解法二:还原问题的思考方法来解答。买圆珠笔后余下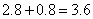 元,买钢笔后余下
元,买钢笔后余下 元,小明带了
元,小明带了 元。所以,选D。考查点:数量关系>数学运算>和差倍比问题>和差倍问题
元。所以,选D。考查点:数量关系>数学运算>和差倍比问题>和差倍问题
22、玉米的正常市场价格为每公斤1.86元到2.18元,近期某地玉米的价格涨至每公斤2.68元。经测算,向市场每投放储备玉米100吨,每公斤玉米价格可下降0.05元。为稳定玉米价格,向该地投放储备玉米的数量不能超过_____。
A: 800吨B: 1080吨C: 1360吨D: 1640吨
参考答案: D 本题解释:正确答案是D考点和差倍比问题解析所求量为投放储备玉米的最大数量,对应正常市场价格的最低价。此时价格差为2.68-1.86=0.82元,而每100吨可降0.05元,因此数量不能超过0.82÷0.05×100=1640吨。故正确答案为D。
23、某地劳动部门租用甲、乙两个教室开展农村实用人才培训。两教室均有5排座位,甲教室每排可坐10人,乙教室每排可坐9人。两教室当月共举办该培训27次,每次培训均座无虚席,当月培训1290人次。问甲教室当月共举办了多少次这项培训?_____
A: 8B: 10C: 12D: 15
参考答案: D 本题解释:正确答案是D考点和差倍比问题解析乙教室可坐9人,可知乙培训过的人数含有因子3,而总的培训人数1290也含有因子3,因此甲教室培训过的人数也必然含有3因子。而甲教室可坐50人,因此要使甲教室培训过的人数也含有3因子,则其举办次数必然含有3因子,因此只有C、D符合。将C选项代入,可知此时乙教室举办过15次培训,其总人数的尾数为5,而甲教室培训的总人数尾数总是为0,因此甲、乙教室的培训人数尾数为5,不符合要求。故正确答案为D。秒杀技由题意,甲教室每次培训50人,乙教室每次培训45,假设甲乙的次数分别为X、Y,则可得50X+45Y=1290,观察等式可知45Y的尾数必然为0,因此Y必然为偶数,从而X为奇数,仅D符合。故正确答案为D。
24、甲、乙两堆煤共重78吨,从甲堆运出  到乙堆,则乙堆与甲堆的重量比是
到乙堆,则乙堆与甲堆的重量比是  。原来各有多少吨煤?_____
。原来各有多少吨煤?_____
A: 30,48B: 40,38C: 50,28D: 60,18
参考答案: B 本题解释:参考答案:B题目详解:解法一:设甲堆原来有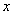 吨,乙堆有
吨,乙堆有 吨。有
吨。有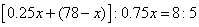 ,得到
,得到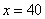 。于是甲堆有40吨煤,乙堆有38吨煤。解法二:将甲乙两堆煤分为13份,则:每份重量为:
。于是甲堆有40吨煤,乙堆有38吨煤。解法二:将甲乙两堆煤分为13份,则:每份重量为: 甲现在的重量为:6×5=30吨甲原来重量为:30÷﹙1-25%﹚=40吨那么乙原来的重量为:78-40=38吨考查点:数量关系>数学运算>和差倍比问题>比例问题
甲现在的重量为:6×5=30吨甲原来重量为:30÷﹙1-25%﹚=40吨那么乙原来的重量为:78-40=38吨考查点:数量关系>数学运算>和差倍比问题>比例问题
25、一个容器中已注满水,有大、中、小三个球。第一次把小球沉入水中,第二次把小球取出。把中球沉入水中,第三次把中球取出,把大球沉入水中,现知道每次从容器中溢出水量的情况是:第一次是第二次的  ,第三次是第二次的1.5倍。求三个球的体积之比。_____
,第三次是第二次的1.5倍。求三个球的体积之比。_____
A:  B:
B:  C:
C:  D:
D: 
参考答案: C 本题解释:参考答案:C题目详解:根据题意,设小球体积为1,则有:第一次溢出的是第二次的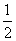 ,说明中球体积是3,第二次溢出的体积是2,由于第三次是第二次的1.5倍,所以第三次溢出的体积是3。一共溢出了1+2+3=6,这是大球的体积。因此这三球的体积之比为6:3:1。所以,选C。考查点:数量关系>数学运算>和差倍比问题>比例问题
,说明中球体积是3,第二次溢出的体积是2,由于第三次是第二次的1.5倍,所以第三次溢出的体积是3。一共溢出了1+2+3=6,这是大球的体积。因此这三球的体积之比为6:3:1。所以,选C。考查点:数量关系>数学运算>和差倍比问题>比例问题
26、已知小明与小强步行的速度比是2:3,小强与小刚步行的速度比是4:5。已知小刚10分钟比小明多走420米,那么小明在20分钟里比小强少走几米?_____
A: 780B: 720C: 480D: 240
参考答案: C 本题解释:参考答案:C题目详解:根据题意,把小强步行速度的看作单位“1”,则有:小明是小强的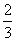 ,小刚是小强的
,小刚是小强的 ,所以小强10分钟行
,所以小强10分钟行 米。小明比小强少行
米。小明比小强少行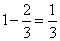 ,所以,小明在20分钟里比小强少走
,所以,小明在20分钟里比小强少走 米。所以,选C。考查点:数量关系>数学运算>和差倍比问题>比例问题
米。所以,选C。考查点:数量关系>数学运算>和差倍比问题>比例问题
27、已知甲、乙两人共有260本书,其中甲的书有13%是专业书,乙的书有12.5%是专业书,问甲有多少本非专业书?_____
A: 75B: 87C: 174D: 67
参考答案: B 本题解释:正确答案是B考点和差倍比问题解析由“甲的书有13%是专业书”可知,甲的专业书=甲的书×13%,所以甲的书是100的倍数,甲的非专业书是87的倍数,排除A、D。由“乙的书有12.5%是专业书”可知,乙的专业书=乙的书×12.5%=乙的书×1/8,所以乙的书是8的倍数。结合选项,若甲的专业书为174本,则甲有200本书,那么乙的书有60本,不是8的倍数,排除C,故正确答案为B。标签数字特性
28、某城市共有A、B、C、D、E五个区,A区人口是全市人口的5/17,B区人口是A区人口的2/5,C区人口是D区和E区人口总数的5/8,A区比C区多3万人,全市共有多少万人?_____
A: 20.4B: 30.6C: 34.5D: 44.2
参考答案: D 本题解释:正确答案是D考点和差倍比问题解析由A区人口是全市人口的5/17,将全市人口看做17份,则A区有5份,B区有2份,于是C、D、E三区共有10份,而在此三区中,C区人口是D区和E区人口总数的5/8,也即C区人口是此三区人口总数的5/13,因此C区人口为(5/13×10)份,于是A区比C区多5-50/13=15/13份,此部分人口数为3万人,于是全市共有3÷15/13×17=44.2(万人)。故正确答案为D。标签赋值思想
29、某公司职员25人,每季度共发放劳保费用15000元,已知每个男职员每季度发580元,每个女职员比每个男职员每季度多发50元,该公司男、女职员之比是多少?_____
A: 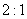 B:
B: 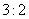 C:
C: 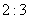 D:
D: 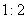
参考答案: B 本题解释:参考答案:B题目详解:假设25人都是男职员,那么共发放 元,比15000元少500元。这多出来的500元是女员工的。因此女员工有
元,比15000元少500元。这多出来的500元是女员工的。因此女员工有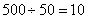 人,即男员工是15人。那么男、女员工人数比是
人,即男员工是15人。那么男、女员工人数比是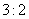 。考查点:数量关系>数学运算>和差倍比问题>比例问题
。考查点:数量关系>数学运算>和差倍比问题>比例问题
30、今年某高校数学系毕业生为60名,其中70%是男生,男生中有1/3选择继续攻读硕士学位,女生选择攻读硕士学位的人数比例是男生选择攻读硕士学位人数比例的一半,那么该系选择攻读硕士学位的毕业生共有_____。
A: 15位B: 19位C: 17位D: 21位
参考答案: C 本题解释:正确答案是C考点和差倍比问题解析根据题意,毕业生中有30%是女生,攻读硕士学位的占1/6,因此该系攻读硕士学位的毕业生共有60×70%×1/3+60×30%×1/6=17位,故正确答案为C。
31、某班在一次植树活动中,平均每人植树7.5棵,若男女生分别计算,则男生平均每人植树9棵,女生平均每人植树5棵,该班男生占全班人数的_____。
A: 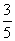 B:
B: 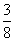 C:
C: 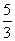 D:
D: 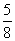
参考答案: D 本题解释:参考答案 题目详解:解法一:根据题意,设男生有
题目详解:解法一:根据题意,设男生有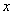 人,女生有
人,女生有 人,可列方程为:
人,可列方程为: ,即得
,即得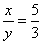 。所以男生占到全班人数的
。所以男生占到全班人数的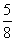 。解法二:把全班人数设为1,把四个答案带入,解的是D(该解析由用户“成与不成皆非”于2011-04-1313:32:02贡献,感谢感谢!)考查点:数量关系>数学运算>和差倍比问题>比例问题
。解法二:把全班人数设为1,把四个答案带入,解的是D(该解析由用户“成与不成皆非”于2011-04-1313:32:02贡献,感谢感谢!)考查点:数量关系>数学运算>和差倍比问题>比例问题
32、甲、乙两种含金样品熔成合金,如甲的重量是乙的一半,得到含金  的合金;如甲的重量是乙的3.5倍,得到含金
的合金;如甲的重量是乙的3.5倍,得到含金  的合金。那么乙的含金量为_____。
的合金。那么乙的含金量为_____。
A:  B:
B:  C:
C:  D:
D: 
参考答案: A 本题解释:参考答案:A题目详解:解法一:设甲的含金量为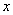 ,乙的含金量为
,乙的含金量为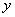 ,可列方程:
,可列方程: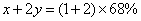
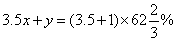 解得
解得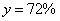 。所以,选A。解法二:设甲重量单位1,含量a,乙含量是b
。所以,选A。解法二:设甲重量单位1,含量a,乙含量是b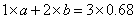
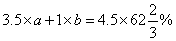 解得,
解得,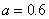 ,
, 所以,选A。考查点:数量关系>数学运算>和差倍比问题>比例问题
所以,选A。考查点:数量关系>数学运算>和差倍比问题>比例问题
33、甲、乙两位学生原计划每天自学的时间相同,若甲每天增加自学时间半小时,乙每天减少自学时间半小时,则乙自学6天的时间仅相当于甲自学一天的时间。问:甲、乙原计划每天自学多少分钟?_____
A: 42B: 48C: 56D: 64
参考答案: A 本题解释:参考答案:A题目详解:解法一:原来二者时间相同,现在甲每天增加自学时间半小时,乙每天减少自学时间半小时,甲比乙多自学一个小时,乙自学6天的时间仅相等于甲自学一天的时间,甲是乙的6倍,差倍问题。乙每天减少半小时后的自学时间为: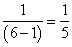 小时=12分钟,乙原计划每天自学时间为:30+12=42分钟,甲原计划每天自学时间为:12×6-30=42分钟。解法二:原来时间相同,现甲多半小时,乙少半小时,现在的两数差是(30+30)=60分钟,现在的差数差是(6-1)=5倍,这样可求出现乙每天自学的时间,加上30分钟,可得原计划每天自学时间。即:(30+30)÷(6-1)+30=12+30=42(分钟)。所以,选A。考查点:数量关系>数学运算>和差倍比问题>和差倍问题
小时=12分钟,乙原计划每天自学时间为:30+12=42分钟,甲原计划每天自学时间为:12×6-30=42分钟。解法二:原来时间相同,现甲多半小时,乙少半小时,现在的两数差是(30+30)=60分钟,现在的差数差是(6-1)=5倍,这样可求出现乙每天自学的时间,加上30分钟,可得原计划每天自学时间。即:(30+30)÷(6-1)+30=12+30=42(分钟)。所以,选A。考查点:数量关系>数学运算>和差倍比问题>和差倍问题
34、高分必看:和差倍比问题秒杀技视频讲解小红把平时节省下来的全部五分硬币先围成一个三角形,正好用完,后来又改围城一个正方形,也正好用完。如果正方形的每条边比三角形的每条边少用5枚硬币,则小红所有五分硬币的总价值是_____。
A: 1元B: 2元C: 3元D: 4元
参考答案: C 本题解释:正确答案是C考点和差倍比问题解析设围成三角形每条边上有x个硬币,每个顶点重复1次,则围成三角形硬币总数为3(x-1)个,同理围成正方形硬币总数为4(x-5-1),3(x-1)=4(x-5-1),解得x=21,因此共有硬币3×(21-1)=60个,总价值3元。故正确答案为C。秒杀技围成三角形正好用完说明硬币总数一定是3的倍数,因此只有C符合。
35、甲、乙、丙三人,参加一次考试,共得260分,已知甲得分的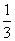 ,乙得分的
,乙得分的 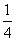 与丙得分的一半减去22分都相等,那么丙得分多少?_____
与丙得分的一半减去22分都相等,那么丙得分多少?_____
A: 72B: 96C: 88D: 92
参考答案: D 本题解释:参考答案 题目详解:解法一:根据题意,设甲得
题目详解:解法一:根据题意,设甲得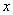 分,乙得
分,乙得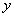 分,丙得
分,丙得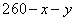 ,可列方程:
,可列方程: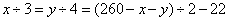 ,解得,
,解得,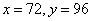 。则丙得分为92。所以,选D解法二:如果丙的分少44分,则丙的一半与甲的
。则丙得分为92。所以,选D解法二:如果丙的分少44分,则丙的一半与甲的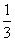 、乙的
、乙的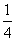 相等,此时总分是:
相等,此时总分是: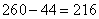 分。设丙是二份,则甲是3份,乙是4份,则:每份是:
分。设丙是二份,则甲是3份,乙是4份,则:每份是: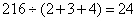 ,即丙是:
,即丙是: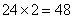 分,那么丙原来的分是:
分,那么丙原来的分是: 分。考查点:数量关系>数学运算>和差倍比问题>和差倍问题
分。考查点:数量关系>数学运算>和差倍比问题>和差倍问题