1、某次考试100道选择题，每做对一题得1.5分，不做或做错一题扣1分，小李共得100分，那么他答错多少题_____
A: 20B: 25C: 30D: 80
参考答案: A 本题解释:答案：A 解析：不做或做错的题目为（100×1.5-100）÷（1.5+1）=20。

2、某月刊杂志，定价2.5元，劳资处一些人订全年，其余人订半年，共需510元，如果订全年的改订半年，订半年的改订全年，共需300元，劳资处共多少人？_____
A: 20B: 19C: 18 D: 17
参考答案: C 本题解释: 【解析】本题用解方程的方法也可以解答，但是速度较慢。由题意可知，如果劳资处所有人都订一年半的话，总计810元;而单人订一年半的月刊需元;所以共有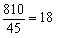人。故选C。

3、法学院200名学生,每人至少辅修法医学、心理学和经济学三项中的一项。其中,辅修法医学的学生有103人,辅修心理学的学生有129人,辅修经济学的有88人。三科全都选择的有16人。只选择法医学和心理学的有30人,只选择法医学和经济学的有7人,那么只选择心理学和经济学的学生有_____人。
A: 51B: 35C: 67D: 83
参考答案: A 本题解释:【解析】设只选择心理学和经济学的学生人数为x,根据题干要求画出关系图,通过观察可列出等式:103+129+88-30-7-x-l6×2=200,解得x=51,即有51人只选择辅修心理学和经济学。答案为A。

4、甲、乙、丙三人共做了183道数学题，乙做的题比丙的2倍少4题，甲做的题比丙的3倍多7题，求甲做的题比乙多多少?_____
A: 67B: 41C: 26D: 30
参考答案: B 本题解释:B【解析】设丙共做x题，则甲做了（3x+7）题，乙做了（2x-4）题，由题意可得：x+（3x+7）+（2x-4）=183,x=30。故甲做了97题，乙做了56题，所以甲比乙多做97-56=41（题）。

5、某地劳动部门租用甲、乙两个教室开展农村实用人才培训。两教室均有5排座位，甲教室每排可坐10人，乙教室每排可坐9人。两教室当月共举办该培训27次，每次培训均座无虚席，当月培训1290人次。问甲教室当月共举办了多少次这项培训? _____
A: 8B: 10C: 12D: 15
参考答案: D 本题解释:【解析】D。本题可直接看出答案，乙教室一次45人，共有1290人，所以乙次数一定为偶数，又因为一共27次，所以甲一定为奇数，直接选15。

6、桌面上有两个半径分别为2厘米和40厘米的圆环，让小圆环沿着大圆环外边缘滚动一圈，则小圆环滚动的圈数是：_____
A: 9B: 25C: 49D: 81
参考答案: B 本题解释:【答案解析】如果两人不调头走，两人相遇需要1350÷1000÷(4+5)×60=9分钟。如果以初始方向为正方向，则两个人分别走了1、-3、5、-7、……分钟的路程，由于9=1-3+5-7+9-11+13-15+17，则出发后1+3+5+7+9+11+13+15+17=81分钟两人相遇。

7、甲、乙两地相距100千米，张先骑摩托车从甲出发，1小时后李驾驶汽车从甲出发，两人同时到达乙地。摩托车开始速度是50千米/小时，中途减速为40千米/小时。汽车速度是80千米/小时。汽车曾在途中停驶10分钟，那么张驾驶的摩托车减速时是在他出发后的多少小时?_____
A: 1B: 3/2C: 1/3D: 2
参考答案: C 本题解释: C解析：汽车行驶100千米需100÷80=5/4（小时），所以摩托车行驶了5/4+1+1/6=29/12（小时）。如果摩托车一直以40千米/小时的速度行驶，29/12小时可行驶96（2/3）千米，与100千米相差10/3千米。所以一开始用50千米/小时的速度行驶了10/3÷（50-40）=1/3（小时）。故本题选C.

8、教室里有若干学生，走了10名女生后，男生是女生人数的2倍，又走了9名男生后，女生是男生人数的5倍。问：最初有多少名女生?_____
A: 15B: 12C: 10D: 9
参考答案: A 本题解释:A【解析】设最初有x名女生，则男生的数量为2(x-10)，由题意可列等式x-10=5[2(x-10)-9]，可得x=15。故选A。

9、一个慢钟每小时比标准时间慢5分钟，一个快钟每小时比标准时间快3分钟。如果将两个钟同时调到标准时间，在24个小时内的某个时间，慢钟显示7:50，快钟显示9:10。那么此时的标准时间应该是什么?_____
A: 8:20B: 8:30C: 8:40D: 8:50
参考答案: C 本题解释:C.【解析】这是一道快慢钟问题。快钟每小时比慢钟快8分钟，而7:50与9:10之间相差80分钟，则此时距离将两个钟调成标准时间为80÷8=10个小时，10个小时的时间，慢钟共少走了5×10=50分钟，则标准时间应该为8:40。因此，本题的正确答案为C选项。

10、一段路程分为上坡、平路、下坡，三段路程长之比依次是1∶2∶3。小龙走各段路程所用时间之比依次是4∶5∶6。已知他上坡时速度为每小时3千米，路程全长是50千米，小龙走完全程用多少小时?_____
A: 10(5/12)B: 12C: 14(1/12)D: 10
参考答案: A 本题解释:A解析：上坡、平路、下坡的速度之比是：14∶25∶36=5∶8∶10平路速度为：3×8/5=24/5（千米/小时）下坡速度为：3×10/5=6（千米/小时）上坡路程为：50×1/（1+2+3）=50/6=25/3（千米）平路路程为：50×2/（1+2+3）=50/3（千米）下坡路程为：50×3/（1+2+3）=25（千米）小龙走完全程用的时间为：25/3÷3+50/3÷24/5+25÷6=10（5/12）（小时）故本题选A。

11、某水果店经销一种销售成本为每千克40元的水果。据市场分析，若按每千克50元销售，一个月能售出500千克；销售单价每涨1元，月销售量就减少10千克。水果店想在月销售成本不超过10000元的情况下，使得月销售利润最大，则定价应为每千克多少元？_____
A: 65B: 70C: 75D: 80
参考答案: C 本题解释:当销售单价定为每千克2元时，月销售量为：500—10×（χ一50）=1000一1Oχ，每千克的销售利润为（χ一40）元，所以月销售利润为：Y=（χ一40）（1000一1Oχ）=一1Oχ2+1400χ-40000=一10（χ一70）2+9000，因为月销售成本不超过10000元，所以40×（1000一1Oχ）≤10000，解得χ≥75。因为二次函数Y=一10（χ一70）2+9000的对称轴为χ=70，χ=75时离对称轴最近，此时Y取最大值，为8750。故本题正确答案为C。

12、(101+103+…+199)-(90+92+…+188)=_____。
A: 100　B: 199　C: 550　D: 990
参考答案: C 本题解释:C[解析]提取公因式法。101-90=11，103-92=11，……，199-188=11，总计有50个这样的算式，所以50×11=550，选择C。

13、某单位职工24人中，有女性11人，已婚的16人。在已婚的16人中有女性6人。问这个单位的未婚男性有多少人? _____
A: 1B: 3C: 9D: 12
参考答案: B 本题解释: 【答案】B。解析：易知该单位有男性13人，其中已婚的有10人，故未婚的有3人，选B。

14、小红把平时节省下来的全部五分硬币先围成一个正三角形，正好用完，后来又改围成一个正方形，也正好用完。如果正方形的每条边比三角形的每条边少用5枚硬币，则小红所有五分硬币的总价值是_____。
A: 1元 B: 2元 C: 3元 D: 4元
参考答案: C 本题解释:C。【解析】设三角形每条边X，正方形为Y，那么Y=X-5，同时由于硬币个数相同，那么3X=4Y，如此可以算出X=20，则硬币共有3×20=60个，硬币为5分硬币，那么总价值是5×60=300（分），得出结果。

15、小张数一篇文章的字数，二个二个一数最后剩一个，三个三个一数最后剩一个，四个四个一数最后剩一个，五个五个一数最后剩一个，六个六个一数最后剩一个，七个七个一数最后剩一个，则这篇文章共有多少字?_____
A: 501B: 457C: 421D: 365
参考答案: C 本题解释: 【解析】C。这道题实际只要考虑五个五个一数最后剩一个，三个三个一数最后剩一个，即可。这两个最好思考。只有501与421一幕了然，除以5余1。而501能被3整除，只有42。

16、某企业发奖金是根据利润提成的。利润低于或等于10万元时可提成10%,低于或等于20万元时,高于10万元的部分按7.5%提成;高于20万元时,高于20万元的部分按5%提成。当利润额为40万元时,应发放奖金多少万元?_____
A: 2B: 2.75C: 3D: 4.5
参考答案: B 本题解释:【答案】B。解析:40万元的利润,10万元按10%计算利润,10万元按7.5%计算利润,再20万元按5%计算利润。共10×10%+10×7.5%+20×5%=2.75万元。

17、某三年制普通初中连续六年的在校生人数分别为：X1,X2,X3,X4,X5,X6.假设该校所有学生都能顺利毕业，那么前三年的入学学生总数与后三年的入学学生总数之差为_____
A: (X1+X2+X3)-(X4+X5+X6) B: X1-X4C: X3-X6 D: (X3-X1)-(X6-X4)
参考答案: C 本题解释:【解析】C.考查整体思维。前三年入学学生人数本质上就是第三年的在校生人数X3（第三年在校生的初三、初二、初一分别为前三年的入学人数），类似的，X6即为后三年的入学人数。故答案为X3-X6.

18、用3、9、0、1、8、5分别组成一个最大的六位数与最小的六位数，它们的差是_____。
A: 15125B: 849420C: 786780D: 881721
参考答案: D 本题解释:D最大的数为985310，最小的数为103589，故它们的差为881721。

19、小明和小强从400米环形跑道的同一点出发，背向而行。当他们第一次相遇时，小明转身往回跑;再次相遇时，小强转身往回跑;以后的每次相遇分别是小明和小强两人交替调转方向。小明每秒跑3米，小强每秒跑5米，则在两人第30次相遇时。小明共跑了多少米? _____
A: 11250B: 13550C: 10050D: 12220
参考答案: A 本题解释:A。两人相向运动，经过400÷（3+5）=50秒相遇，之后小明转身，两人做追及运动，经过400÷（5-2）=200秒第二次相遇;接着两人又做相向运动，经过50秒相遇，再做追及运动，经过200秒相遇，以此类推，第30次相遇共用30÷2×（50+200）=3750秒，则小明共跑了3×3750=11250米。

20、甲、乙沿同一公路相向而行，甲的速度是乙的1.5倍，已知甲上午8点经过邮局，乙上午10点经过邮局。问：甲乙在中途何时相遇? _____
A: 8点48分B: 8点30分C: 9点D: 9点10分
参考答案: A 本题解释:A。【解析】设乙的速度为x，甲就是1.5x，当甲8点到邮局时，乙离邮局还有2个小时的路程（2x），甲乙走完2x路程需要2x/（1.5x+x）=4/5小时=48分钟，加上8点，就是8点48分相遇。

21、河道赛道长120米，水流速度为2米／秒，甲船速度为6米／秒，乙船速度为4米／秒。比赛进行两次往返，甲、乙同时从起点出发，先顺水航行，问多少秒后甲、乙船第二次迎面相遇？_____
A: 48 B: 50 C: 52 D: 54
参考答案: C 本题解释: C。

22、4只小鸟飞入4个不同的笼子里去，每只小鸟都有自己的一个笼子(不同的鸟，笼子也不相同)，每个笼子只能飞进一只鸟。若都不飞进自己的笼子里去，有多少种不同的飞法?_____。
A: 7B: 8C: 9D: 10
参考答案: C 本题解释:C。本题属于计数问题。本题是排列组合中的错位问题，根据对错位问题数字的记忆，答案应为9种。所以选择C选项。计算过程：设四只小鸟为1，2，3，4，则1有3个笼可选择，不妨假设1进了2号笼，则2也有3个笼可选择，不妨设2进了3号笼，则剩下鸟3、4和笼1、4只有一种选择。所以一共有3×3=9种。

23、过长方体一侧面的两条对角线交点，与下底面四个顶点连得一四棱锥，则四棱锥与长方体的体积比为多少？_____
A: 1∶8B: 1∶6C: 1∶4D: 1∶3
参考答案: B 本题解释:【答案】B。解析：等底等高时，椎体体积是柱体的1/3。而这里椎体的高是柱体高的一半，因此该四棱锥与长方体的体积之比为1：6，故正确答案为B。

24、纸上写着2、4、6三个整数，改变其中任意一个，将它改写成为其他两数之和减1，这样继续下去，最后可以得到的是_____。
A: 595、228、368B: 44、95、50C: 103、109、211D: 159、321、163
参考答案: A 本题解释:A。

25、三边长均为整数且最大边长为2009的三角形共有多少个？_____
A: 1008016 B: 1009020 C: 1010025 D: 2019045
参考答案: C 本题解释: C。根据三角形的构成原理，可知最大边长为2009时，另两边的和大于2009，差小于2009，则两边≤2009且≥1，则可知介于最长边与最短边之间的那条中边的长度必≥1005且≤2009。中边为1005时，另一边=1005，1种可能；中边为1006时，另一边=1004，1005，1006，共3种可能；中边为1007时，另一边=1003，1004，1005，1006，1007，共5种可能；……中边为2009时，另一边=1~2009，共2009种可能。因此三角形总和=1+3+5+…+2007+2009=1005（1+2009）/2=1010025种。所以答案为C项。

26、蜘蛛有8条腿，蜻蜓有6条腿和2对翅膀，蝉有6条腿和1对翅膀，现在这三种小虫共18只，有118条腿和18对翅膀，蜘蛛，蜻蜓，蝉各几只_____
A: 5、5、8B: 5、5、7C: 6、7、5D: 7、5、6
参考答案: A 本题解释:【答案】A。解析：这是道复杂的“鸡兔同笼”问题，首先，蜻蜓和蝉都是6条腿，数腿的时候可以放在一起考虑，因此蜘蛛有（118—6×18）÷（8—6）=5只，因此蜻蜓和蝉共有18—5=13只，从而蜻蜓有（18—1×13）÷（2—1）=5只，蝉有13—5=8只。

27、某天晚上一警局18%的女警官值班。如果那天晚上有180个警官值班，其中一半是女警官，问该警局有多少女警官？_____
A: 900B: 180C: 270D: 500
参考答案: D 本题解释:【解析】D。180个警官中的一半是女警官，则值班的女警官为90个，而这90个女警官占总数的女警官18％，可知女警官有500人。

28、商店卖气枪子弹，每粒1分钱，每粒4分钱，每10粒7分钱，每20粒1角2分钱。小明的钱至多能买73粒，小刚的钱至多能买87粒.小明和小刚的钱合起来能买多少粒? _____
A: 160B: 165C: 170D: 175
参考答案: B 本题解释:【答案】B。解析：小明子弹73颗，可知买了3个20粒，1个10粒，3个1粒，共有46分钱;同理小刚买了4个20粒，1个5粒，2个l粒，共有54分钱。两人共有100分钱，可以买8个20粒，1个5粒，共卖165粒。

29、用数字0，1，2(既可全用也可不全用)组成的非零自然数，按从小到大排列，问“1010”排在第几个?_____
A: 30B: 31C: 32D: 33
参考答案: A 本题解释:本题实际求由0，1，2构成的数字中，小于1010的有多少个。位数不固定，先按位数分类，再对每类进行计数。显然组成的非零一位数有2个;两位数有2×3=6（个）;三位数有2×3×3=18（个）;四位数中比1010小的为1000，1001，1002共计3个。故1010排在第30位。故选A。

30、某网站针对年底上映的两部贺岁电影进行调查，在接受调查的160人中，看过《未来警察》的有91人，看过《杜拉拉升职记》的有59人，22人两部电影都看过，那么，两部电影都没看过的有多少人?_____
A: 32人B: 12人C: 42人D: 10人
参考答案: A 本题解释: A 解析：设两部电影都没看过的有x人，依题意可得：91+59-22+x=160，解得x=32。即有32人两部电影都没看过，答案为A。

31、某商场有7箱饼干，每箱装的包数相同，如果从每箱里拿出25包饼干，那么，7个箱里剩下的饼干包数相当于原来的2箱饼干，原来每箱饼干有多少包?_____。
A: 25B: 30C: 50D: 35
参考答案: D 本题解释:【解析】比较简单，可以直接列方程：7(X-25)=2X，所以X=35，选D。

32、甲、乙、丙三队要完成A，B两项工程，B工程工作量比A工程的工作量多1/4 ，甲、乙、丙三队单独完成A工程所需时间分别是20天、24天、30天。为了同时完成这两项工程，先派甲队做A工程，乙、丙两队共同做B工程，经过几天后，又调丙队与甲队共同完成A工程，那么，丙队甲队合做了多少天? _____
A: 18B: 15C: 10D: 3
参考答案: D 本题解释:【解析】D。解析：三队完成这项工程一共用了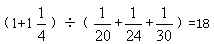天，乙队一直在做B工程，一共做了 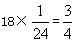，则B工程剩下的 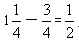为丙做的，故丙队与乙队合做了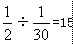天，与甲队合做了18-15=3天。

33、某人同时购买2年期、5年期和10年期三种国债，投资额的比为5：3：2。后又以与前次相同的投资总额全部购买5年期国债，则此人两次对5年期国债的投资额占两次总投资的比例的_____。
A: 3/5B: 7/10C: 3/4D: 13/20
参考答案: D

34、甲、乙有数量相同的萝卜，甲打算卖1元2个，乙打算卖1元3个，如甲、乙二人一起按2元5个卖全部的萝卜，总收入会比预想的1个人少4元，两人共有多少萝卜？_____
A: 420B: 120C: 360D: 240
参考答案: D 本题解释:D。

35、下列可以分解为三个质数相乘的最小的三位数是_____。
A: 100B: 102C: 104D: 105
参考答案: B 本题解释:【答案】B。解析：直接代入各选项求解。题目要求找出符合条件的最小的三位数，则从数值较小的选项开始验证。A项，100＝2×2×5×5，不符合题意。B项，102＝2×3×17，符合题意。C、D项的三位数即使可分解为三个质数相乘，数值上也大于B项的102，因此不作考虑。故正确答案为B。

36、甲、乙两地有一座桥，甲、乙两人分别从甲、乙两地同时出发，3小时在桥中间相遇，如果甲加快速度，每小时多行2千米，而乙提前0.5小时出发，则仍旧在桥中间相遇；如果甲延迟0.5小时出发，乙每小时少走2千米，还会在桥中间相遇，则甲、乙相距（）千米。
A: 60B: 64C: 72D: 80
参考答案: C 本题解释:【答案】C。解析：设甲、乙两人的速度分别为x、y。因为甲乙都是在桥上相遇，因此每次甲走的路程都为3x，乙每次走的路程都为3y。列方程：3x/（x+2）=2.5，3y/（y-2）=3.5，解之得x=10，y=14.A、B之间的路程等于甲乙两人3小时的路程和，即（10+14）X3=72.因此，本题答案选择C选项。

37、某工厂有学徒工、熟练工、技师共80名，每天完成480件产品的任务。已知每天学徒工完成2件，熟练工完成6件，技师完成7件，且学徒工和熟练工完成的量相等，则该厂技师人数是熟练工人数的_____倍。
A: 6 B: 8 C: 10 D: 12
参考答案: D 本题解释:D。列方程组。设学徒工、熟练工、技师分别有X,Y,Z名。则有：X+Y+Z=802X+6Y+7Z=4802X=6Y得到：X=15,Y=5,Z=60,所以Z∶Y=60∶5=12。选D。

38、某产品售价为67.1元，在采用新技术生产节约10%成本之后，售价不变，利润可比原来翻一番。则该产品最初的成本为_______元。_____
A: 51.2 B: 54.9 C: 61 D: 62.5
参考答案: C 本题解释:【解析】C.本题可采用方程法。设该产品最初的成本为元。由题意得：67.1-0.9x=2（67.1-x），解得x=61.因此该产品最初的成本为61元。

39、一百张牌抽掉奇数牌，然后再抽掉剩下牌中位于奇数位的牌……如此最后剩下的一张是原来100张牌排序中的第几张呢？_____
A: 63 B: 64 C: 65 D: 66
参考答案: B 本题解释:B

40、在2011年世界产权组织公布的公司全球专利申请排名中，中国中兴公司提交了2826项专利申请，日本松下公司申请了2463项，中国华为公司申请了1831项，分别排名前3位，从这三个公司申请的专利中至少拿出多少项专利，才能保证拿出的专利一定有2110项是同一公司申请的专利？_____
A: 6049B: 6050C: 6327D: 6328
参考答案: B 本题解释:【答案】B。解析：最值问题。最不利的情况数+1=2109+2109+1831+1=6050;选项尾数不同，可以考虑尾数法。

41、哥哥的年龄和妹妹现在的年龄一样时，妹妹是9岁。妹妹的年龄和哥哥现在的年龄一样时，哥哥是24岁。问妹妹现在的年龄是多少岁?_____
A: 14B: 15C: 17D: 20
参考答案: A 本题解释:答案：A【解析】由题意可得妹妹与哥哥岁数差为（24-9）÷3=5（岁），故妹妹现在的年龄为5+9=14（岁）。

42、某原料供应商对购买其原料的顾客实行如下优惠措施：①一次购买金额不超过1万元，不予优惠;②一次购买金额超过1万元，但不超过3万元，给九折优惠;③一次购买金额超过3万元，其中3万元九折优惠，超过3万元部分八折优惠。某厂因库容原因，第一次在该供应商处购买原料付款7800元，第二次购买付款26100元，如果他一次购买同样数量的原料，可以少付：_____
A: 1460元B: 1540元C: 3780元D: 4360元
参考答案: A 本题解释:【解析】A。第一次购买原料付款7800元，原料的总价值应为7800元，第二次购买时付款26100元，原料的总价值应为26100÷0.9=29000元。如果要将两次购买变成一次购买，则总价值应为7800+29000=36800元，而应该付款额为30000×0.9+6800×0.8=32440元，一次性购买比分两次购买可以节约7800+26100-32440=1460元。

43、：_____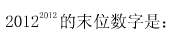
A: 2B: 4C: 6D: 8
参考答案: C 本题解释:

44、甲、乙、丙、丁四个人比赛打羽毛球，每两个都要赛一场，已知甲胜了丁，并且甲、乙、丙三人胜的场数相同，那么丁胜了几场？_____
A: 6 B: 0 C: 12 D: 3
参考答案: B 本题解释:【解析】B。每人至多赛3场，排除A、C。甲胜丁，则丁至少输1场，排除D。

45、一果农想将一块平整的正方形土地分割为四块小土地，并将果树均匀整齐地种在土地的所有边界上，且在每块土地的四个角上都种上一棵果树，该果农未经细算就购买了60颗果树，如果仍按上述想法种植，那他至少多买了_____棵果树。 B: 3C: 6D: 15
参考答案: B 本题解释:【答案解析】本题可利用整除特征性求解，分割成4个小正方形后共有9个顶点，12条边，设每条边(不算顶点)种x棵树，则可种12x+9棵，使总棵树小于60的最大x为4，此时可种57棵树，剩余3棵，所以正确答案为B项。

46、某城市居民用水价格为：每户每月不超过5吨的部分按4元/吨收取，超过5吨不超过10吨的部分按6元/吨收取，超过10吨的部分按8元/吨收取。某户居民两个月共交水费108元，则该户居民这两个月用水总量最多为多少吨?_____
A: 21B: 24C: 17.25D: 21.33
参考答案: A 本题解释:【解析】A。水量越大，费用越高，所以要用水最多，所以每个月应该用满10吨，所以总吨数为20+（108-100）/8=21.

47、将一块三角形绿地沿一条直线分成两个区域，一块为三角形，一块为梯形，已知分出的三角形区域的面积为1.2亩，梯形区域的上、下底边分别为80米、240米，问分出的梯形区域的面积为多少亩?_____
A: 9.6B: 11.2C: 10.8D: 12.0
参考答案: A 本题解释:A。

48、某单位举行“庆祝建党90周年”知识抢答赛，总共50道抢答题。比赛规定：答对1题得3分，答错1题扣1分，不抢答得0分。小军在比赛中抢答了20道题，要使最后得分不少于50分，则小军至少要答对_____道题。
A: 16B: 17C: 18D: 19
参考答案: C 本题解释:假设答对2题，取最坏情形，剩下都答错，则答错20—x题，总分不少于50则有3x-（20-z）≥50，求得x≥17.5，取最小值为18。

49、某班共有50名学生参加数学和外语两科考试，已知数学成绩及格的有40人，外语成绩及格的有25人，据此可知数学成绩及格而外语成绩不及格者_____。
A: 至少有10人B: 至少有15人C: 有20人D: 至多有30人
参考答案: B 本题解释:答案：B【解析】这是一个集合问题，首先可排除答案D，因为与已知条件“外语及格25人”即“外语不及格25人”不符;其次排除C，因为仅以外语及格率为50%推算数学及格者（40人）中外语不及格人数为40×50%=20（人），缺乏依据，实际上，数学及格者中外语不及格的人数至少为25-（50-40）=15人，答案为B。

50、真分数a/7化为小数后，如果从小数点后第一位数字开始连续若干数字之和是1992，那么A的值是_____。
A: 6B: 5C: 7D: 8
参考答案: A 本题解释:【答案解析】：由于除7不能整除的的数结果会是‘142857’的循环(这个可以自己测算一下)，1+4+2+8+5+7=27，1992/27余数为21，重循环里边可知8+5+7+1=21，所以8571会多算一遍(多重复的一遍，一定在靠近小数点的位置上)，则小数点后第一位为8，因此a为6。

51、张家和李家都使用90米的篱笆围成了长方形的菜园，已知李家的长方形菜园的长边比张家短5米，但是菜园面积却比张家大50平方米，则李家的长方形菜园面积为_____。
A: 550平方米B: 500平方米C: 450平方米D: 400平方米
参考答案: B 本题解释:【答案】B。解析：缺少的量为张家和李家菜园的具体长宽，可用方程法。设李家菜园长边为x米，则其短边长为45-x米；张家菜园长边为x+5米，其短边长为40-x，根据题意：x（45-x）-（x+5）×（40-x）=50，可解得x=25，李家菜园面积为x（45-x）=25×20=500。故本题答案为B选项。

52、地球表面的陆地面积和海洋面积之比是29︰71，其中陆地的四分之三在北半球，那么南、北半球海洋面积之比是_____
A: 284︰29B: 113︰55C: 371︰313D: 171︰113
参考答案: D 本题解释:【解析】D。根据题干中的比例关系，可以推断出南、北半球的海洋面积之比为：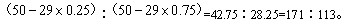

53、Ａ、Ｂ、Ｃ、Ｄ、Ｅ是5个不同的整数，两两相加的和共有8个不同的数值。分别是17、25、28、31、34、39、42、45，则这5个数中能被6整除的有几个?_____
A: 0B: 1C: 2D: 3
参考答案: C 本题解释:C【解析】不妨设A<B<C<D<E，则容易知道A+B=17，A+C=25，C+E=42，D+E=45，只要知道B+C的值就可以了。B+C只可能是剩下的28,31,34,39中之一。由于(A+B)+(A+C)+(B+C)=2(A+B+C)为偶数，而A+B和A+C都为奇数，故B+C为偶数，B+C只能是28或34；又B+C<B+D<B+E<C+E<D+E，即比B+C大的数至少有4个，故B+C不能是34或39，综合可知，B+C=28，于是可解A=7，B=10，C=18，D=21，E=24，能被6整除的数有18和24两个，选择C选项。

54、比-5大-7的数是_____。
A: -3B: 2C: -12D: -7
参考答案: C 本题解释: C [解析] -5+（-7）=-12。故本题选C。

55、有一件工作，丙单独做需10小时完成;乙、丙合作需4小时完成。甲2小时完成的工作量，乙需要3小时才能完成。现在这件工作由丙独做，他从清晨5时开工，必须在中午12时完工。甲、乙二人应帮助丙工作多少时间才能使丙准时完成工作?_____
A: 4/5小时B: 1小时C: 4/3小时D: 2小时
参考答案: A 本题解释:

56、甲、乙二人2小时共加工54个零件，甲加工3小时的零件比乙加工4小时的零件还多4个。甲每小时加工多少个零件?_____
A: 11B: 16C: 22D: 32
参考答案: B 本题解释: 【解析】B。解法一、设俩人速度分别为x、y，则2x+2y=54，3x-4y=4，解得x=16;解法二、从第一句话知D不对。从第二句话中知甲每小时加工的零件是4的倍数。

57、有两只相同的大桶和一只空杯子，甲桶装牛奶，乙桶装糖水，先从甲桶内取出一杯牛奶倒入乙桶，再从乙桶取出一杯糖水和牛奶的混合液倒人甲桶，请问，此时甲桶内的糖水多还是乙桶内的牛奶多?_____。
A: 无法判定B: 甲桶糖水多C: 乙桶牛奶多D: 一样多
参考答案: D 本题解释:D【精析】假设乙桶内有N杯糖水，从甲中取出1杯牛奶倒入乙桶，乙桶中有l杯牛奶和N杯糖水。均匀后，再从乙桶取出一杯糖水和牛奶的混合物倒入甲桶，这杯混合物中有牛奶1/N+1杯有糖水N/N+1杯,因此乙桶中剩余的牛奶有N/N+1杯，而倒入甲桶中的糖水也有而N/N+1杯。甲桶内的糖水和乙桶内的牛奶一样多。

58、有41个学生要坐船过河，渡口处只有一只能载4人的小船(无船工)，他们要全部渡过河去，至少要使用这只小船渡河多少次？_____
A: 23B: 24C: 27D: 26
参考答案: C 本题解释:【答案】C。解析：套用公式，过河次数＝（41－1）/（4－1）＝13.33，过河次数为整数，13＜13.33＜14，要使所有人都过河，只能取14。所求次数为单程次数，来回总共14×2－1＝27次（最后一次过河不再返回）。故正确答案为C。公式：过河问题中每次过河都需要有一个人将船划回来，而最后一次过河不再需要划回来。N个人过河，船最多载M人，则过河次数为（N－1）/（M－1）。过河次数指单程次数，注意最后一次过河不需要人划回来，总次数＝单程次数×2－1。

59、从12时到13时，钟的时针与分针可成直角的机会有_____。
A: 1次B: 2次C: 3次D: 4次
参考答案: B 本题解释:【答案解析】一个小时内成直角只有两次，选B。

60、有一个矩形花园,长比宽多30米,现在花园的四周铺等宽的环路。已知路的面积是800M2,路的外周长是180m,问路宽是多少米?_____
A: 4B: 5C: 6D: 3
参考答案: B 本题解释:【答案】B。解析:设小矩形的宽是x,则长是x+30;设路宽是y,则大矩形的宽是x+2,大矩形的长是x+30+2y,已知条件可表示为(x+2y)(x+30+27)-x(x+30)=800和2(x+2y+x+30+2y)=180,解得y=5米。

61、一个边长为8的正立方体，由若干个边长为1的正立方体组成，现在要将大立方体表面涂漆，问一共有多少小立方体被涂上了颜色？_____
A: 296 B: 324 C: 328 D: 384
参考答案: A 本题解释:A【解析】思路一：其实不管如何出，公式就是=>边长（大正方形的边长）3-（边长（大正方形的边长）-2） 3 。思路二：一个面64个，总共6个面，64×6=384个，八个角上的正方体特殊，多算了2×8=16个，其它边上的，多算了6×4×2+4×6=72，所以384-16-72=296。

62、一个人到书店购买了一本书和一本杂志，在付钱时，他把书的定价中的个位上的数字和十位上的看反了，准备付21元取货。售货员说∶“您应该付39元才对。”请问书比杂志贵多少钱?_____
A: 20B: 21C: 23 0D: 24
参考答案: C 本题解释:【答案】C。解析：数字看反前后，书价相差18，说明十位和个位数字相差为2，总价为39，故书价只能是31，则杂志的价格是8.相差23。

63、时钟指示2点15分，它的时针和分针所成的锐角是多少度?_____
A: 45度B: 30度C: 25度50分D: 22度30分
参考答案: D 本题解释:【答案解析】解析：追击问题的变形，2点时，时针分针成60度，即路程差为60度，时针每分钟走1/2度，分针每分钟走6度，时针分针速度差为6-1/2=11/2，15分钟后时针分针的路程差为60-(11/2)×15=-45/2，即此时分针已超过时针22度30分。

64、某人在公共汽车上发现一个小偷向相反方向步行，10秒钟后他下车去追小偷，如果他的速度比小偷快一倍，比汽车慢4/5，则此人追上小偷需要_____。
A: 20秒B: 50秒C: 95秒D: 110秒
参考答案: D 本题解释:答案：D【解析】设某人速度为v，则小偷速为0.5v，汽车速为5v，10秒钟内，与小偷相差（0.5+5）v×10=55v，追求时速差为0.5v，所以所需时间为110秒。

65、某种奖券的号码有9位，如果奖券至少有两个非零数字并且从左边第一个非零数字起，每个数字小于它右边的数字，就称这样的号码为“中奖号码”，请问该种奖券的“中奖号码”有_____。
A: 512个B: 502个C: 206个D: 196个
参考答案: B 本题解释:【解析】解一：号码1—9各出现1或0次，按递增顺序排列（前面补0），共产生2×2×2×2×2×2×2×2×2=29个号码，其中无非零数字或仅有1个非零数字的应予排除（共有10种）。所以中奖号码共有512-10=502个。故本题正确答案为B。解二：中奖号码至少有两个非零数字且从左边第一个非零数字起，每个数字小于它右边的数字，则可得出：C29+C39+C49+C59+C69+C79+C89+C99=502，故选B。

66、在一次有四个局参加的工作会议中，土地局与财政局参加的人数比为5∶4，国税局与地税局参加的人数比为25∶9，土地局与地税局参加人数的比为10∶3，如果国税局有50人参加，土地局有多少人参加？_____
A: 25 B: 48 C: 60 D: 63
参考答案: C 本题解释: 【解析】根据以上比例关系，可得出土地局︰地税局︰国税局=30︰9︰25，所以土地局有60人参加。所以选C。

67、足球比赛的记分规则为：胜一场得3分;平一场得1分;负一场得0分。一个队打了14场，负5场，共得19分，那么这个队胜了几场?_____
A: 3B: 4C: 5D: 6
参考答案: C 本题解释:C解析：设这个队胜了a场，平了b场，则3a+b=19，a+b=14-5=9;解得a=5。

68、软广告是指广告主并不直接介绍商品、服务，而是通过在报纸、杂志、网络、电视节目、电影等宣传载体上插入带有主观指导倾向性的文章、画面、短片，或者通过赞助社会活动、公益事业等方式来达到提升广告主企业品牌形象和知名度，从而促进广告主销售的一种广告形式。根据上述定义，下列不属于软广告的是_____。
A: 美国西屋电气公司在《时代周刊》上刊登了一篇文章，把本年度有关公司的各种正面报道汇集在一起，并冠以总标题《一年来本公司的各种好消息》B: 英国石油公司曾制作、发布了一个短片，名为“我们让挖掘机停下，让5000棵树的生命延续”C: 走进武汉菜大学的教室，可以发现黑板旁边有一则告示：“TC1友好提醒：为了您和他人，进入教室前请把手机关掉！”D: 美国通用汽车在好莱坞大片《变形金刚》中投入了3亿美元，影片放映前播出了3分钟的雪佛兰汽车短片，并在片尾打出了“未来，为我而来”的品牌口号
参考答案: A 本题解释:A项是通过在杂志上登载带有主观指导倾向性的文章，来提高企业的品牌形象和知名度；B项是通过短片来宣扬自己的公益事业，并树立企业的社会形象；C项，这则告示并未直接介绍自己的产品，不会引起人们的反感，可以在不知不觉中对受众产生正面影响，提升企业品牌形象和知名度。D项，短片是在电影放映前播出的，并不是在电影中插入，而且是直接介绍雪佛兰汽车的，因而属于硬广告。故本题选D。

69、5人的体重之和是423斤，他们的体重都是整数，并且各不相同，则体重最轻的人最重可能重_____
A: 80斤 B: 82斤 C: 84斤 D: 86斤
参考答案: B 本题解释:B。【解析】5个80斤的则为400斤，剩余23斤，分一下。 从0、1、2、3、4、5、6、7中选，最轻只有选2了，如选3，则3、4、5、6、7加起来超过23。所以为82斤。

70、某班有35个学生，每个学生至少参加英语小组、语文小组、数学小组中的一个课外活动小组。现已知参加英语小组的有17人，参加语文小组的有30人，参加数学小组的有13人。如果有5个学生三个小组全参加了，问有多少个学生只参加了一个小组？_____
A: 15人B: 16人C: 17人D: 18人
参考答案: A 本题解释:A【解析】利用三交集公式A+B+C=AUBUC+AnB+BnC+AnC-AnBnC（AnBnC是指语文，数学，英语三个都参加的人，AUBUC是只总人数），A+B+C=17+30+13，AnBnC=5，AUBUC=35，所求为AUBUC-（AnB+BnC+AnC）+AnBnC。 方便解法：参加一个小组的为x人，两个小组的为y人，x+y+5=35，x+2y+3×5=17+30+13，x=15。

71、一个三位数除以43，商是a，余数是b，则a+b的最大值是：_____
A: 957B: 64C: 56D: 33
参考答案: B

72、小明和姐姐用2013年的台历做游戏，他们将12个月每一天的日历一一揭下，背面朝上放在一个盒子里，姐姐让小明一次性帮她柚出一张任意月份的30号或者31号。问小明一次至少应抽出多少张日历，才能保证满足姐姐的要求？_____
A: 346 B: 347 C: 348 D: 349
参考答案: C 本题解释:【答案】C。

73、一个车队有三辆汽车， 担负着五家工厂的运输任务，这五家工厂分别需要 7、9、4、10、6 名装卸工，共计 36 名;如果安排一部分装卸工跟车装卸，则不需要那么多装卸工，而只需要在装卸任务较多的工厂再安排一些装卸工就能完成装卸任务。那么在这种情况下，总共至少需要_____名装卸工才能保证各厂的装卸需求?_____
A: 26　　B: 27　　C: 28　　D: 29
参考答案: A 本题解释:【答案】A[解析]要求最少，那么三辆车分别装五家工厂里面最大的三个需求量，则可以满足条件，分别装10、9、7， 所以是10+9+7=26，选A。

74、某日小李发现日历有好几天没有翻，就一次翻了6张，这6天的日期加起来的数字和是141，他翻的第一页是几号？_____
A: 18 B: 21 C: 23 D: 24
参考答案: B 本题解释: 【解析】B。设第一张的日期为X，则可得方程X+X+1+X+2+X+3+X+4+X+5=141，解得X=21，所以选答案B。

75、Ａ，Ｂ两村庄分别在一条公路L的两侧，A到L的距离|AC|为1公里，B到L的距离|BD|为2公里，C,D两处相距6公里，欲在公路某处建一个垃圾站，使得A,B两个村庄到此处处理垃圾都比较方便，应建在离C处多少公里_____
A: 2.75B: 3.25C: 2D: 3
参考答案: C 本题解释:答案： C 解析：连接AB，交公路L于点E，E点就是A、B两个村庄到此处处理垃圾都比较方便的地方，三角形ACE相似于三角形BDE，则AC⊥CE=BD⊥DE,而CE+DE=6,AC=1,BD=2,解得CE=2,故应建在离C处2公里。

76、一条线段中间另有6个点，则这8个点可以构成多少条线段?_____
A: 15B: 12C: 28D: 36
参考答案: C 本题解释:C。相邻两点构成线段8-1=7中间隔一点构成线段8-2=6类推距离最远两点（两端点）构成线段8-7=1，1+2+3+.+6+7=（1+7）*7/2=28选C

77、某人上午8点要上班，可是发现家里的闹钟停在了6点10分，他上足发条但忘了对表就急急忙忙的上班去了，到公司一看还提前了10分钟。中午12点下班后，回到家一看，闹钟才11点整，假定此人上班、下班在路上用的时间相同，那么他家的闹钟停了多少分钟?_____
A: 100B: 90C: 80D: 70
参考答案: C 本题解释:【解析】C。由题意知：6时10分+闹钟停的时间=7时50分;11时+闹钟停的时间=12时+下班后路上走的时间，所以闹钟停的时间+上班时间=7时50分-6时10分=100分钟，闹钟停的时间上班时间=12时-11时=60分，故闹钟停的时间为（100+60）÷2=80分钟。

78、152个球，放入若干个同样的箱子中，一个箱子最少放10个，最多放20个，且各个箱子的球数均不相同，问有多少种放法?(不计箱子的排列，即两种放法，经过箱子的重新排列后，是一样的，就算一种放法)_____
A: 1B: 7C: 12D: 24
参考答案: A 本题解释:A【解析】 设箱子个数为m，因为每只箱子的球数均不相同，最少放10个，最多放20个，所以m≤20-10+1=11。如果m=11，那么球的总数≥10×11+（0+1+2+…+10）=110+55>152，所以m≤10。如果m≤9，那么球的总数≤10×9+（10+9+8+…+2）=90+54=144<152，所以m=10在m=10时，10×10+（10+9+…+1）=155=152+3，所以一个箱子放10个球，其余箱子分别放11，12，14，15，16，17，18，19，20个球，总数恰好为152，而且符合要求的放法也只有这一种。故本题正确答案为A。

79、共计33个三角形和四边形，有111个角，则四边形的个数为_____。
A: 10B: 11C: 12D: 13
参考答案: C 本题解释: C [解析] 设四边形的个数为x，由题意可得：4x+（33-x）×3=111，解得x=12，即应该有12个四边形。故本题选C。

80、共有20个玩具交给小王手工制作完成。规定，制作的玩具每合格一个得5元，不合格一个扣2元，未完成的不得不扣。最后小王共收到56元，那么他制作的玩具中，不合格的共有_____个。
A: 2B: 3C: 5D: 7
参考答案: A 本题解释:【答案】A。解析：设小王制作合格玩具x个，不合格玩具y个，未完成的有z个。则x＋y＋z＝20，5x－2y＝56。为不定方程组，将选项代入验证，仅当y＝2时，x与z有正整数解。故正确答案为A。

81、今年父亲年龄是儿子年龄的10倍，6年后父亲年龄是儿子年龄的4倍，则今年父亲、儿子的年龄分别是_____。
A: 60岁，6岁 B: 50岁，5岁C: 40岁，4岁 D: 30岁，3岁
参考答案: D

82、50名同学面向老师站成一行。老师先让大家从左至右按1，2，3，…依次报数;再让报数是4的倍数的同学向后转，接着又让报数是6的倍数的同学向后转。问：现在面向老师的同学还有多少名?_____
A: 30B: 34C: 36D: 38
参考答案: D 本题解释: D【解析】 第一次报4的倍数的12名同学向后转后，在报6的倍数的8名同学中，面向老师和背向老师的各4名。分析如下：报4的倍数的同学分别报4，8，12，16，20，24，28，…，48;报6的倍数的同学分别报6，12，18，24，30，…，48;第二次报6的倍数的同学中有4名同学的报数与第一次报4的倍数的同学相同，故两次报数结束后，先前4名背向老师的同学又面向老师，另外4名同学则背向老师。故可推出，背向老师的同学有12名，面向老师的同学有38名。因此，本题正确答案为D。

83、四个学生做加法练习，任写一个六位数，然后把个位数字(不等于0)移到这个数的最左边产生一个新的六位数，最后把这个新六位数与原数相加，分别得到以下四个六位数。则哪个结果有可能正确? _____
A: 172536B: 568741C: 620708D: 845267
参考答案: C 本题解释:

84、小赵、小王、小李和小陈四人，其中每三个人的岁数之和分别为65、68、62、75其中年龄最小的是多少岁?_____
A: 15 B: 16 C: 17 D: 18
参考答案: A 本题解释:A【解析】设四人年龄从大到小依次为A、B、C、D则有A+B+C+=75，B+C+D=62，A+B+D=68，A+C+D=65将四个“年龄和”相加可得3（A+B+C+D）=65+68+62+75=270则A+B+C+D=90故D的年龄为90-75=15岁，故应选择A选项。

85、有一批资料，甲机单独复印需11时，乙机单独复印需13时，当甲乙两台复印机同时复印时，由于相互干扰，每小时两台共少印28张，现在两台复印机同时复印了6小时15分钟才完成，那么这批资料共有多少张？_____
A: 2860B: 3146C: 3432D: 3575
参考答案: D 本题解释:【答案】D。解析：

86、一个四边形广场，它的四边长分别是60米，72米，84米，96米，现在在四边上植树，四角需种树，而且每两棵树的间隔相等，那么，至少要种多少棵树?_____
A: 22B: 25C: 26D: 30
参考答案: C 本题解释:【解析】C。4个数字都相差12，可将树的间隔设为12米，可种树(60+72+84+96)/12=5+6+7+8=26，选C。

87、在一次国际美食大赛中，中、法、日、俄四国的评委对一道菜品进行打分。中国评委和法国评委给出的平均分是94，法国评委和日本评委给出的平均分是90，日本评委和俄罗斯评委给出的平均分是92，那么中国评委和俄罗斯评委给出的平均分是_____。
A: 93分B: 94分C: 96分D: 98分
参考答案: C 本题解释:C【解析】设中、法、日、俄四国的评委给出的分数分别是A、B、C、D，根据题意可知：A+B=94×2，B+C=90×2，C+D=92×2，又因为A+D=（A+B）+（C+D）-（B+C）=94×2+92×2-90×2=（94+92-90）×2=96×2所以中国评委和俄国评委给出的平均分是96分，本题正确答案为C。

88、加油站有150吨汽油和102吨柴油，每天销售12吨汽油和7吨柴油。问多少天后，剩下的柴油是剩下的汽油的3倍？_____
A: 9B: 10C: 11D: 12
参考答案: D 本题解释:【答案】D。解析：假设x天，汽油还剩150-12x，柴油还剩102-7x，102-7x=3（150-12x），解得x=12，答案为D。

89、从0，1，2，7，9五个数字中任选四个不重复的数字，组成的最大四位数和最小四位数的差是_____。
A: 8442B: 8694　C: 8740D: 9694
参考答案: B 本题解释:答案：B。由题意可得：最大的四位数为9721，最小的四位数为1027，故两者的差是9721-1027=8694。

90、8.01×1.24+8.02×1.23+8.03×1.22的整数部分是多少?_____
A: 24B: 27C: 29D: 33
参考答案: C 本题解释:答案：C【解析】由8.03×1.22<8.02×1.23<8.01×1.24得：8.01×1.24+8.02×1.23+8.03×1.22<8.01×1.24×3<8×1.25×3=30。8.01×1.24+8.02×1.23+8.03×1.22>8×（1.24+1.23+1.22）=8×3.69=29.52。所以，所求的整数部分为29。故选C。

91、某村有甲乙两个生产小组，总共50人，其中青年人共13人。甲组中青年人与老年人的比例是2∶3，乙组中青年人与老年人的比例是1∶5，甲组中青年人的人数是：_____
A: 5人B: 6人C: 8人D: 12人
参考答案: C 本题解释:【答案】C。解析：设甲组人数为5x,乙组人数为6y。有，解得x=4。因此甲组青年人的人数为8。

92、现有边长1米的一个木质正方体，已知将其放入水里，将有0.6米浸入水中。如果将分割成边长0.25米的小正方体，并将所有的小正方体都放入水中，直接和水接触的表面积总量为_____。
A: 3.4平方米B: 9.6平方米C: 13.6平方米D: 16平方米
参考答案: C 本题解释:本题属于面积问题。因为把边长为1米的正方体木块置于水中有0.6米浸入水中，所以当将其分割为边长0.25米的正方体木块置于水中时，其浸入水中的高度为3/20米。则可以计算出其中一个分割后的正方体木块与水的接触面积为：（1/4）×（1/4）+4×（1/4）×（3/20）=1/16+3/20,又因为边长1米的正方体可以分割为64个边长为O.25米的正方体，所以题中所求面积为：64×（1/16+3/20）=13.6（平方米）。正确答案为C。

93、某玩具店同时卖出一个拼装玩具和一架遥控飞机，拼装玩具66元，遥控飞机120元，拼装玩具赚了10%，而遥控飞机亏本20%，则这个商店卖出这两个玩具赚钱或是亏本多少?_____
A: 赚了12元B: 赚了24元C: 亏了14元D: 亏了24元
参考答案: D 本题解释:【答案】D。解析：二者成本分别为66÷（1+10%）=60元、120÷（1-20%）=150元，成本合计为60+150=210元，亏了210-66-120=24元。

94、甲地到乙地，步行比骑车速度慢75%,骑车比公交慢50%，如果一个人坐公交从甲地到乙地共用1个半小时，问：骑车从甲地到乙地多长时间? _____
A: 10分钟B: 20 分钟C: 30分钟D: 40分钟
参考答案: B 本题解释:B。设骑车的速度为x公里/小时，则步行速度为0.25x公里/小时，公车的速度为2x公里/小时。设甲乙两地距离为L公里，则L/0.25x+L/2x=1.5，得到L/x=1/3小时=20分钟，则骑车从甲地到乙地需20分钟。

95、一条长度为30米、宽度为3米的未划停车位的路边，最差的情况也可以停2米宽、3米长的汽车多少辆?_____
A: 5辆B: 7辆C: 8辆D: l5辆
参考答案: A 本题解释:【解析】分三种情况:第一种:汽车如果与道路垂直。每辆车的车距应尽可能的大，但距离必须小于2米（否则可以再停一辆），当两辆车的车距为2米时，最少可停（30-2）÷（2+2）=7（辆），那么最差的情况下至少可以停8辆车;第二种:汽车如果与道路平行。每辆车的车距应尽可能的大，但距离小于3米，当两辆车的车距为3米时，最少可停（30-3）÷（3+3）=4.5（辆），即停5辆。第三种:汽车与道路有平行与垂直两种情况并存，则停的汽车数量应介于5辆和8辆之间。而题干是问的最差的情况，故最少停5辆车。

96、有面积为1平方米、4平方米、9平方米、16平方米的正方形地毯各10块，现有面积为25平方米的正方形房间需用以上地毯来铺设，要求地毯互不重叠且而好铺满。问最少需几块地毯? _____
A: 6块B: 8块C: 10块D: 12块
参考答案: B 本题解释:最少需地毯块数,即尽量用大面积的地毯,25=16+9×1 ——10块25=9+3×4+4×1——8块25=4×4+9×1 ——13块,所以最小块数为8.具体是一块9平方米，三块4平方米。四块1平方米，选B。

97、一段路程分为上坡、平路、下坡三段，路程长之比依次是1∶2∶3。小龙走各段路程所用时间之比依次是4∶5∶6。已知他上坡时速度为每小时3千米，路程全长是50千米，小龙走完全程用多少小时?_____
A: 10(5/12)B: 12C: 14(1/12)D: 10
参考答案: A 本题解释: A解析：上坡、平路、下坡的速度之比是：14∶25∶36=5∶8∶10平路速度为：3×8/5=24/5（千米/小时）下坡速度为：3×10/5=6（千米/小时）上坡路程为：50×1/（1+2+3）=50/6=25/3（千米）平路路程为：50×2/（1+2+3）=50/3（千米）下坡路程为：50×3/（1+2+3）=25（千米）25/3÷3+50/3÷24/5+25÷6=10（5/12）（小时）故本题选A。

98、一根木杆，第一次截去了全长的1/2，第二次截去所剩木杆的1/3，第三次截去所剩木杆的1/4，第四次截去所剩木杆的1/5，这时量得所剩木杆长为6厘米。问：木杆原来的长是多少厘米?_____
A: 15B: 26C: 30D: 60
参考答案: C 本题解释: C解析： 6÷（1-1/5）÷（1-1/4）÷（1-1/3）÷（1-1/2）6÷（4/5×3/4×2/3×1/2）6÷1/5=30（厘米）故本题选C。

99、有一根长240米的绳子，从某一端开始每隔4米作一个记号，每隔6米也作一个记号。然后将标有记号的地方剪断，则绳子共剪成_____段。
A: 40B: 60C: 80D: 81
参考答案: C 本题解释:【答案】C。解析：容斥原理，每隔4米作一个记号，则作记号数为240÷4－1＝59；每隔6米作一个记号，则作记号数为240÷6－1＝39；其中每隔12米的记号重复被作两次，类似的记号数为240÷12－1＝19。因此做记号总数为59＋39－19＝79，即绳子被剪成80段。故正确答案为C。两集合容斥原理公式：|A∪B|＝|A|＋|B|－|A∩B|

100、有A、B两种商品，如果A的利润增加20% ，B的利润减少10% ，那么A、B两商品的利润就相同了。问原来A商品的利润是B商品利润的百分之几?_____
A: 80%B: 70%C: 85%D: 75%
参考答案: D 本题解释:D