微信搜索关注"91考试网"公众号,领30元,获取公务员、事业编、教师等考试资料40G!
1、李大夫去山里给一位病人出诊,他下午1点离开诊所,先走了一段平路,然后爬上了半山腰,给那里的病人看病。半小时后,他沿原路下山回到诊所,下午3点半回到诊所。已知他在平路步行的速度是每小时4千米,上山每小时3千米,下山每小时6千米。请问:李大夫出诊共走了多少路?_____
A: 5千米B: 8千米C: 10千米D: l6千米
参考答案: B 本题解释: 
2、小王和小李6小时共打印了900页文件,小王比小李快50%。请问小王每小时打印多少页文件?_____
A: 60B: 70C: 80D: 90
参考答案: D 本题解释: 【解析】D。设小王每小时打印X页,因为小王比小李快50%,则小李每小时打印为X (1-50%)页,则根据题意可列:6X (1-50%)+6X=900,则X=90。
3、在自然数1至50中,将所有不能被3除尽的数相加,所得的和是_____。
A: 865B: 866C: 867D: 868
参考答案: C 本题解释:正确答案是C考点数列问题解析”1至50,所有不能被3除尽的数相加”,等价于”1到50所有数的和减去能被3整数的项”,所以代求的值为(1+2+……50)-(3+6+……+48)=50×51/2-3×16×17/2=1275-408=867,故正确答案为C。秒杀技”1到50所有数的和”能被3整除,减去所有能被3整除的数后,还能被3整除。所以”不能被3除尽的数的和”能被3整除,选项中只有C满足,故正确答案为C。
4、把一根圆木锯成3段需要8分钟,如果把同样的圆木锯成9段需要多少分钟?_____
A: 24分钟B: 27分钟C: 32分钟D: 36分钟
参考答案: C 本题解释:正确答案是C考点计数模型问题解析圆木锯成三段有2个切口,2个切口需要用时8分钟,锯成9段有8个切口,则8个切口需要用时8÷2×8=32(分钟),故正确答案为C。
5、(2005国家二类,第45题)外语学校有英语、法语、日语教师共27人,其中只能教英语的有8人,只能教日语的有6人,能教英、日语的有5人,能教法、日语的有3人,能教英、法语的有4人,三种都能教的有2人,则只能教法语的有多少人?_____
A: 4人B: 5人C: 6人D: 7人
参考答案: B 本题解释:参考答案:B题目详解:“由中间向外围”进行数据标记,进行简单加减运算,如下图过程所示: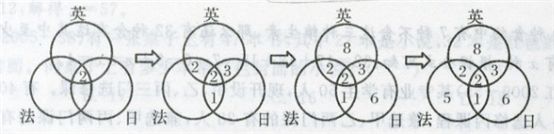 [注释]本题中注意两个非常重要的要点:(1)题中表述的“只能教……”与其他题目可能存在的“能教……”是两个完全不同的概念,标数字的时候切记区别;(2)本题首句表明“这27个人中不存在三种语言都不教的人”,而其他一些题目可能存在三个条件都不满足的情形,计算的时候切记区别。考查点:数量关系>数学运算>容斥原理问题>三个集合容斥关系
[注释]本题中注意两个非常重要的要点:(1)题中表述的“只能教……”与其他题目可能存在的“能教……”是两个完全不同的概念,标数字的时候切记区别;(2)本题首句表明“这27个人中不存在三种语言都不教的人”,而其他一些题目可能存在三个条件都不满足的情形,计算的时候切记区别。考查点:数量关系>数学运算>容斥原理问题>三个集合容斥关系
6、已知小明与小强步行的速度比是2:3,小强与小刚步行的速度比是4:5。已知小刚10分钟比小明多走420米,那么小明在20分钟里比小强少走几米?_____
A: 780B: 720C: 480D: 240
参考答案: C 本题解释:参考答案:C题目详解:根据题意,把小强步行速度的看作单位“1”,则有:小明是小强的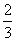 ,小刚是小强的
,小刚是小强的 ,所以小强10分钟行
,所以小强10分钟行 米。小明比小强少行
米。小明比小强少行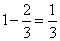 ,所以,小明在20分钟里比小强少走
,所以,小明在20分钟里比小强少走 米。所以,选C。考查点:数量关系>数学运算>和差倍比问题>比例问题
米。所以,选C。考查点:数量关系>数学运算>和差倍比问题>比例问题
7、在一个两位数之间插入一个数字,就变成一个三位数。例如:在72中间插入数字6,就变成了762。有些两位数中间插入数字后所得到的三位数是原来两位数的9倍,下列数字满足条件的是:_____
A: 25 B: 20 C: 18 D: 17
参考答案: A 本题解释:A。【解析】对于这个题来说,首先要判断个位是多少,这个数的个位乘以9以后的个位还等于原来的个位,说明个位只能是0或5,先看0,很快发现不行,因为20×9=180,30×9=270,40×9=360等等,不管是几十乘以9,结果百位总比十位小,所以各位只能是5。略作计算,不难发现:15,25,35,45是满足要求的数。故选A。
8、某国家对居民收入实行下列税率方案;每人每月不超过3000美元的部分按照1%税率征收,超过3000美元不超过6000美元的部分按照X%税率征收,超过6000美元的部分按Y%税率征收(X,Y为整数)。假设该国某居民月收入为6500美元,支付了120美元所得税,则Y为多少_____
A: 6B: 3C: 5D: 4
参考答案: A 本题解释:答案: A 解析:该国某居民月收入为6500美元要交的所得税为3000×1%+3000×X%+(6500-3000-3000)×Y%=120,化简为6X+Y=18,由于6X和18都能被6整除,因此Y也一定能被6整除分析选项,只有A符合。
9、已知甲的13%为14,乙的14%为15,丙的15%为16,丁的16%为17,则甲、乙、丙、丁四个数中最大的数是_____。
A: 甲B: 乙C: 丙D: 丁
参考答案: A 本题解释:正确答案是A考点和差倍比问题解析
10、一个袋子里放有10个小球(其中4个白球,6个黑球),无放回地每次抽取1个,则第二次取到白球的概率是_____。
A: 2/15B: 4/15C: 1/5D: 2/5
参考答案: D 本题解释:正确答案是D考点概率问题解析 秒杀技根据无放回摸球结论:任何一次摸到白球的概率都相等。因此所求第二次摸到白球的概率与第一次摸到白球的概率相等,而后者为2/5。故正确答案为D。
秒杀技根据无放回摸球结论:任何一次摸到白球的概率都相等。因此所求第二次摸到白球的概率与第一次摸到白球的概率相等,而后者为2/5。故正确答案为D。
11、若p和q为质数,且5p+3q=91,则p和q的值为:_____
A: 2,27B: 3,19C: 5,17D: 17,2
参考答案: D 本题解释:参考答案 题目详解:5p+3q=91,∴p、q为一奇一偶,∵p和q为质数,∴p、q中必有一数为2,当p=2时,q=27,27为合数,故舍去,当q=2时,p=17。故p=17,q=2。故答案为:17,2。考查点:数量关系>数学运算>计算问题之数的性质>奇偶性与质合性问题>奇偶性
题目详解:5p+3q=91,∴p、q为一奇一偶,∵p和q为质数,∴p、q中必有一数为2,当p=2时,q=27,27为合数,故舍去,当q=2时,p=17。故p=17,q=2。故答案为:17,2。考查点:数量关系>数学运算>计算问题之数的性质>奇偶性与质合性问题>奇偶性
12、取甲种硫酸300克和乙种硫酸250克,再加水200克,可混合成浓度为50%的硫酸;而取甲种硫酸200克和乙种硫酸150克,再加上纯硫酸200克,可混合成浓度为80%的硫酸。那么,甲、乙两种硫酸的浓度各是多少?_____
A: 75%,60%B: 68%,63%C: 71%,73%D: 59%,65%
参考答案: A 本题解释:【答案】A。解析:
13、三个圆的半径都是5厘米,三个圆两两相交于圆心。求阴影部分的面积之和。_____ 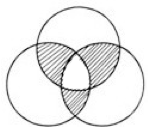
A: 29.25平方厘米B: 33.25平方厘米C: 39.25平方厘米D: 35.35平方厘米
参考答案: C 本题解释:正确答案是C考点几何问题解析使用割补法可知阴影部分的面积相当于半个圆的面积,则可得25π÷2=25×3.14÷2=39.25。故正确答案为C。
14、有20名工人修筑一段公路,计划15天完成。动工3天后抽出5人去其他工地,其余人继续修路。如果每人工作效率不变,那么修完这段公路实际用_____
A: 19天B: 18天C: 17天D: 16天
参考答案: A 本题解释:【答案】A。解析:5人12天完成的工作量分配给15人需要5×12÷15=4天完成,所以修完这段公路实际用15+4=19天。
15、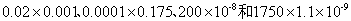 哪个最小?_____
哪个最小?_____
A: 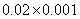 B:
B: 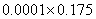 C:
C: 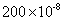 D:
D: 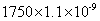
参考答案: D 本题解释:参考答案 题目详解:四个式子分别用科学计数法表示为:
题目详解:四个式子分别用科学计数法表示为: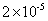 ,
,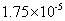 ,
,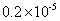 ,
,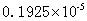 ;则最小的为
;则最小的为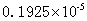 ,即最小的式子为
,即最小的式子为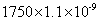 。所以,选D。考查点:数量关系>数学运算>计算问题之算式计算>比较大小问题
。所以,选D。考查点:数量关系>数学运算>计算问题之算式计算>比较大小问题
16、毛毛骑在牛背上过河,他共有甲、乙、丙、丁4头牛,甲过河要2分钟,乙过河要3分钟,丙过河要4分钟,丁过河要5分钟。毛毛每次只能赶2头牛过河,要把4头牛都赶到对岸去,最少要多少分钟? _____
A: 16B: 17C: 18D: 19
参考答案: A 本题解释:A。若要时间最短,则一定要让耗时最长的两头牛同时过河。先骑甲、乙过河,骑甲返回,共用5分钟;再骑丙、丁过河,骑乙返回,共用8分钟;最后再骑甲、乙过河,用3分钟,共用时5+8+3=16分钟。
17、时针与分针两次垂直的间隔有多长时间?_____
A: 32分B: 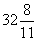 分C: 33分D: 34分
分C: 33分D: 34分
参考答案: B 本题解释:参考答案:B题目详解:解法一:根据公式:时针与分针两次垂直间隔的“静态时间”为30分钟,代入公式算得追及时间为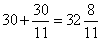 分钟,所以选择B。解法二:根据基本知识点:时针与分针24小时内垂直44次,所以垂直间隔为:
分钟,所以选择B。解法二:根据基本知识点:时针与分针24小时内垂直44次,所以垂直间隔为: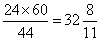 分钟考查点:数量关系>数学运算>特殊情境问题>钟表问题>时针与分针的角度关系
分钟考查点:数量关系>数学运算>特殊情境问题>钟表问题>时针与分针的角度关系
18、_____ 
A: AB: BC: CD: D
参考答案: D 本题解释:正确答案是D考点几何问题解析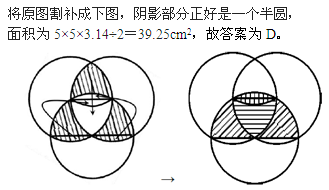
19、某城新修建的一条道路上有12盏路灯,为了节省用电而又不影响正常的照明,可以熄灭其中三盏灯,但两端的灯不能熄灭,也不能熄灭相邻的两盏灯,那么熄灯的方法共有多少种?_____
A: 56B: 64C: 220D: 120
参考答案: A 本题解释:参考答案:A题目详解:12盏路灯,由于两端的灯不能熄灭:因此只有l0盏路灯可以熄灭,熄灭以后剩下7盏亮的和3盏灭的,要使熄灭的灯互不相邻,那么可以用“插空法”:将3盏灭的插到7盏亮的所形成的8个空位中即可满足条件;因此,熄灯的方法有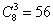 种;所以,选A。考查点:数量关系>数学运算>排列组合问题>常规排列组合问题
种;所以,选A。考查点:数量关系>数学运算>排列组合问题>常规排列组合问题
20、有三块草地,面积分别是5,15,24亩。草地上的草一样厚,而且长得一样快。第一块草地可供10头牛吃30天,第二块草地可供28头牛吃45天,问第三块地可供多少头牛吃80天?_____
A: 42B: 60C: 54D: 72
参考答案: A 本题解释:参考答案:A题目详解:根据题意:此题属于M头牛吃W亩草问题,将单位牧场的牛数代入“N”;单位牧场草的原有存量为y;单位时间草的增长量即自然增长速度为x;第三块地可供牛的头数即消耗变量3为N;代入公式: 所以,选A。考查点:数量关系>数学运算>特殊情境问题>牛儿吃草问题>M头牛吃W亩草问题
所以,选A。考查点:数量关系>数学运算>特殊情境问题>牛儿吃草问题>M头牛吃W亩草问题
21、某网店连续3次下调某款手机的零售价格,每次下调幅度分别为:2.7%、5.5%和4.6%。经过3次调价,该款手机零售价较下调前大约下降了_____。
A: 12.3%B: 12.8%C: 13.3%D: 13.8%
参考答案: A 本题解释:正确答案是A考点经济利润问题解析连续调价三次以后价格为原价的(1-2.7%)×(1-5.5%)×(1-4.6%)>(1-2.7%-5.5%-4.6%),因此下降的价格幅度小于原价的2.7%+5.5%+4.6%=12.8%,故正确答案为A。
22、_____ 
A: AB: BC: CD: D
参考答案: A 本题解释:正确答案是A考点几何问题解析
23、学校举办一次中国象棋比赛,有10名同学参加,比赛采用单循环赛制,每名同学都要与其他9名同学比赛一局。比赛规则,每局棋胜者得2分,负者得0分,平局两人各得1分。比赛结束后,10名同学的得分各不相同,已知:(1)比赛第一名与第二名都是一局都没有输过;(2)前两名的得分总和比第三名多20分;(3)第四名的得分与最后四名的得分和相等。那么,排名第五名的同学的得分是_____。
A: 8分B: 9分C: 10分D: 11分
参考答案: D 本题解释:正确答案是D考点统筹规划问题解析
24、某班有60名学生,在第一次测验中有32人得满分,在第二次测验中有27人得满分。如果两次测验中都没有得满分的学生有17人,那么两次测验中都获得满分的人数是多少?_____
A: 13人B: 14人C: 15人D: 16人
参考答案: D 本题解释:正确答案是D考点容斥原理问题解析本题注意按照得满分得到两个类,进行容斥原理分析。设第一次测验得满分为事件A,第二次测验得满分为事件B,则两次都得满分为A∩B,将其设为x人,得过满分为A∪B。根据公式A∪B=A+B-A∩B可得:60-17=32+27-x解得x=16,因此两次测验中都获得满分的人数是16人,故正确答案为D。
25、某校初一年级共有三个班,一班与二班人数之和为98,一班与三班人数之和为106,二班与三班人数之和为108,则二班人数为多少人?_____
A: 48B: 50C: 58D: 60
参考答案: B 本题解释:正确答案是B考点和差倍比问题解析解析1:由题意设一班、二班、三班分别有a、b、c人,则a+b=98,a+c=106,b+c=108,解之得b=50。故正确答案为B。解析2:由题意一班二班三班共有(98+106+108)/2=156人,所以二班有156-106=50人。故正确答案为B。
26、某企业有甲、乙、丙三个仓库,且都在一条直线上,之间分别相距1千米、3千米,三个仓库里面分别存放货物5吨、4吨、2吨。如果把所有的货物集中到一个仓库,每吨货物每千米运费是90元,请问把货物放在哪个仓库最省钱?_____
A: 甲B: 乙C: 丙D: 甲或乙
参考答案: B 本题解释:B解析:此题遵循“小往大处靠”原则,先把2吨的货物移动到4吨那,这样就相当于有了6吨货物,然后在把5吨的货物也移动到6吨,综上所述,运到乙仓库最省钱。
27、一汽船往返于两码头间,逆流需要10小时,顺流需要6小时。已知船在静水中的速度为12公里/小时。问水流的速度是多少公里/小时?_____
A: 2B: 3C: 4D: 5
参考答案: B 本题解释:参考答案:.B题目详解:根据题意,设水流的速度是x公里/小时,两码头间距离为y公里。确定顺流航行速度:(x+12)公里/小时,确定逆流航行速度:(12-x)公里/小时。则有: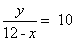 ,
,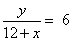 ,解得
,解得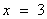 ;所以,选B。考查点:数量关系>数学运算>行程问题>行船问题>基本行船问题
;所以,选B。考查点:数量关系>数学运算>行程问题>行船问题>基本行船问题
28、银行整存整取的年利率是:2年期为2.25%,3年期为2.52%,5年期为2.79%,如果甲、乙二人同时各存入1万元,甲先存2年期,到期后连本带利改存为3年期;乙存5年期。5年后,2人同时取出,那么两人的收益差为多少元?_____
A: 64B: 102C: 155D: 234
参考答案: C 本题解释:C【解析】 甲5年后取出本利和为:10000×(1+2.25%×2)×(1+2.52%×3)=10000×1.045×1.0756=11240(元)乙5年后取出本利和为:10000×(1+2.79%×5)=1000×1.1395=11395由此可见,乙的收益多。11395-11240=155(元)。故选C。
29、南阳中学有语文教师8名、数学教师7名、英语教师5名和体育教师2名。现要从以上四科教师中各选出1名教师去参加培训,问共有几种不同的选法?_____
A: 96种B: 124种C: 382种D: 560种
参考答案: D 本题解释:正确答案是D考点排列组合问题解析 标签公式应用
标签公式应用
30、完成某项工程,甲单独工作需要18小时,乙需要24小时,丙需要30小时。现按甲、乙、丙的顺序轮班工作,每人工作一小时换班。当工程完工时,乙总共干了多少小时?_____
A: 8小时B: 7小时44分C: 7小时D: 6小时48分
参考答案: B 本题解释:正确答案是B考点工程问题解析解析1:设工程总量为360,则甲乙丙的工作效率分别为20、15、12,三人每小时工作总量为47。由题意可知三人轮班即为循环周期问题,用360除以47商7余数为31,甲乙丙轮班每人7小时后,乙继续工作的工作量为31-20=11。所以最终乙总共干了:7小时+11/15×60分=7小时44分,故正确答案为B。解析2:设工程总量为360,则甲乙丙的工作效率分别为20、15、12,甲每小时比乙多干5,乙每小时比丙多干3,因此乙工作时间必定小于24/3=8小时。观察选项有6小时、7小时和8小时,可选7为参考点,甲乙丙轮班每人工作7小时共完成:(20+15+12)×7=329<360,因此乙工作时间在7小时和8小时之间,故正确答案为B。标签赋值思想
31、一个正方体木块放在桌子上,每一面都有一个数,位于对面两个数的和都等于13,小张能看到顶面和两个侧面,看到的三个数和为18;小李能看到顶面和另外两个侧面,看到的三个数的和为24,那么贴着桌子的这一面的数是多少_____
A: 4B: 5C: 6D: 7
参考答案: B 本题解释:【答案】B。解析:小张、小李二人看到的数加起来一共为2组对面加上2倍的顶面,因此顶面为(18+24-13×2)÷2=8,底面为13-8=5.
32、甲班有42名学生,乙班有48名学生,在某次数学考试中按百分制评卷,评卷结果两个班的数学总成绩相同,平均成绩是整数,且都高于80分,请问甲班的平均分与乙班相差多少分呢?_____
A: 12分B: 14分C: 16分D: 18分
参考答案: A 本题解释:参考答案:A题目详解:假设甲乙两班平均分分别为x、y,则: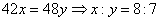 ,不妨假设x=8t,y=7t,则两班平均分相差为t:由题干已知,我们可以得到:
,不妨假设x=8t,y=7t,则两班平均分相差为t:由题干已知,我们可以得到: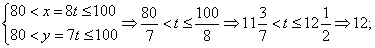 所以,选A。考查点:数量关系>数学运算>计算问题之算式计算>不等式问题>由不等式确定未知量取值范围
所以,选A。考查点:数量关系>数学运算>计算问题之算式计算>不等式问题>由不等式确定未知量取值范围
33、用两根同样长度的铁丝分别圈成圆形和正方形,圆形面积大约是正方形面积的几倍?_____
A: 3/πB: 4/πC: 5/πD: 6/π
参考答案: B 本题解释:正确答案是B考点几何问题解析设圆的半径为r,则正方形的面积为 ,圆形的面积为
,圆形的面积为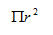 ,所以答案为B。
,所以答案为B。
34、甲、乙、丙三人共做了183道数学题,乙做的题比丙的2倍少4题,甲做的题比丙的3倍多7题,求甲做的题比乙多多少?_____
A: 67B: 41C: 26D: 30
参考答案: B 本题解释:B【解析】设丙共做x题,则甲做了(3x+7)题,乙做了(2x-4)题,由题意可得:x+(3x+7)+(2x-4)=183,x=30。故甲做了97题,乙做了56题,所以甲比乙多做97-56=41(题)。
35、甲从A地步行到B地,出发1小时40分钟后,乙骑自行车也从同地出发,骑了10公里时追到甲。于是,甲改骑乙的自行车前进,共经5小时到达B地,这恰是甲步行全程所需时间的一半。问骑自行车的速度是多少公里/小时?_____
A: 12B: 10C: 16D: 15
参考答案: A 本题解释:正确答案是A考点行程问题解析根据已知,10公里的路程骑车比步行省1小时40分(100分钟)。甲骑车后比全程步行省了5小时(前段路程是步行,没有节省),也就是300分钟,说明甲后来骑车了3×10=30公里。从A到B的路程总共是10+30=40公里。全程骑车共需要300-100=200分钟=10/3小时,所以骑车速度=40/(10/3)=12公里/小时,故正确答案为A。
36、在平面直角坐标系中,如果点P(3a-9,1-a)在第三象限内,且横坐标、纵坐标都是整数,则点P的坐标是_____。
A: (一1.一3)B: (一3,一1)C: (一3,2)D: (一2,一3)
参考答案: B 本题解释:B【解析】第三象限内的值都是负值,因此可得 。且P点横纵坐标都是整数,因此2,所以P点坐标是(一3,一1)。
。且P点横纵坐标都是整数,因此2,所以P点坐标是(一3,一1)。
37、任意取一个大于50的自然数,如果它是偶数,就除以2;如果它是奇数,就将它乘3之后再加1。这样反复运算,最终结果是多少?_____ B: 1C: 2D: 3
参考答案: B 本题解释:参考答案:B题目详解:解法一:采用特殊值法:取64,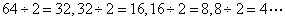 ,最后结果是1;取55,
,最后结果是1;取55,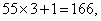 变成偶数,按照题目要求计算后,最后结果是1;所以,选B。解法二:采用排除法:若为
变成偶数,按照题目要求计算后,最后结果是1;所以,选B。解法二:采用排除法:若为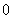 :最后结果显然不能为0,(在本题中通过乘除之后结果不可能为0);若为2:按题意,需再计算一次,得到1;若为3:需继续运算,最后结果也将是1。所以,选B。考查点:数量关系>数学运算>计算问题之数的性质>奇偶性与质合性问题>奇偶性
:最后结果显然不能为0,(在本题中通过乘除之后结果不可能为0);若为2:按题意,需再计算一次,得到1;若为3:需继续运算,最后结果也将是1。所以,选B。考查点:数量关系>数学运算>计算问题之数的性质>奇偶性与质合性问题>奇偶性
38、(2009浙江,第50题)“红星”啤酒开展“7个空瓶换一瓶啤酒”的优惠促销活动。现在已知张先生在活动促销期间共喝掉347瓶“红星”啤酒,问张先生最少用钱买了多少瓶啤酒?_____
A: 296瓶B: 298瓶C: 300瓶D: 302瓶
参考答案: B 本题解释:参考答案:B题目详解: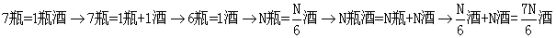 可知
可知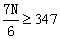 ,解得
,解得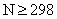 考查点:数量关系>数学运算>统筹问题>空瓶换酒问题
考查点:数量关系>数学运算>统筹问题>空瓶换酒问题
39、共计33个三角形和四边形,有111个角,则四边形的个数为_____。
A: 10B: 11C: 12D: 13
参考答案: C 本题解释: C [解析] 设四边形的个数为x,由题意可得:4x+(33-x)×3=111,解得x=12,即应该有12个四边形。故本题选C。
40、已知29832983…298302能被18整除,那么n的最小值是_____。
A: 4B: 5C: 6D: 7
参考答案: A 本题解释:【解析】18=2×9,这个多位数的个位上是2,满足被2整除,因此,只需考虑个位数字之和能否被9整除的问题。(2+9+8+3)×n+0+2=22n+2是9的倍数,22×4+2=90=9×10,那么n的最小值为4。
41、杂货店分三次进了一些货物,已知每一次的进货单价都是上一次的80%,且第一次的进货单价为5元。已知这些货物恰好能够排成一个三层的空心方阵,且最内层、中间层和最外层恰好分别是第一、二、三次所进的货物,且最外层每边有7个货物。现要保证20%利润率的情况下,杂货店应该将货物至少定为多少元?_____
A: 3.90B: 4.12C: 4.36D: 4.52
参考答案: D 本题解释:【解析】D。三次的单价分别为5元、5×80%=4元、4×80%=3.2元。最外层有货物(7-1)x4=24个,中间层有24-8=16个,最内层有I6-8=8个。所以总进价为3.2x24+4xl6+5x8=l80.8元,要保证20%的利润率,货物定价为180.8x(1+20%)÷(24+16+8)=4.52元。
42、20+19-18-17+16+15-14-13+12+11···+4+3-2-1=_____。
A: 10B: 15C: 19D: 20
参考答案: D 本题解释:【答案】D。解析:解析1:原式=(20-18)+(19-17)+(16-14)+(15-13)+···+(4-2)+(3-1)=2+2+2+2+···+2+2=2×10=20。故正确答案为D。解析2:原式=20+(19-18-17+16)+(15-14-13+12)+…+(3-2-1)=20。故正确答案为D。
43、(2008陕西,第16题)一项工程,工作效率提高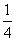 ,完成这项工程的时间将由原来的10小时缩短到几小时?_____
,完成这项工程的时间将由原来的10小时缩短到几小时?_____
A: 4B: 8C: 12D: 16
参考答案: B 本题解释:参考答案:B题目详解:假设原来工作效率为4,工作总量应该为: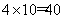 ,工作效率提高
,工作效率提高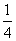 后变为:
后变为: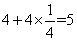 ,时间缩短到:
,时间缩短到: (小时)。所以,选B。考查点:数量关系>数学运算>工程问题>单独完工问题
(小时)。所以,选B。考查点:数量关系>数学运算>工程问题>单独完工问题
44、一根绳子对折三次后,从中剪断,共剪成几段绳子?_____
A: 9B: 6C: 5D: 3
参考答案: A 本题解释:正确答案是A考点计数模型问题解析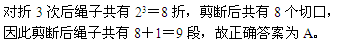
45、3颗气象卫星与地心距离相等,并可同时覆盖全球地表,现假设地球半径为R,则3颗卫星距地球最短距离为_____。
A: RB: 2RC: R/2D: 2R/3
参考答案: A 本题解释:正确答案是A考点几何问题解析 故正确答案为A。
故正确答案为A。
46、(2008北京)甲杯中有浓度为 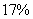 的溶液400克,乙杯中有浓度为
的溶液400克,乙杯中有浓度为 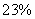 的溶液600克。现在从甲、乙两杯中取出相同总量的溶液,把从甲杯中取出的倒人乙杯中,把从乙杯中取出的倒人甲杯中,使甲、乙两杯溶液的浓度相同。现在两杯溶液的浓度是_____
的溶液600克。现在从甲、乙两杯中取出相同总量的溶液,把从甲杯中取出的倒人乙杯中,把从乙杯中取出的倒人甲杯中,使甲、乙两杯溶液的浓度相同。现在两杯溶液的浓度是_____
A:  B:
B: 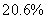 C:
C: 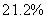 D:
D: 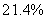
参考答案: B 本题解释:参考答案:B题目详解:解法一:依题意:无论怎样混合,根据最后溶液状态可知,整个过程相当于将甲、乙两杯溶液混合在一起,因此最终两杯溶液的浓度为: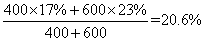 ;所以,选B。解法二:先求出从甲、乙两杯中分别取出的质量m:
;所以,选B。解法二:先求出从甲、乙两杯中分别取出的质量m: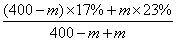
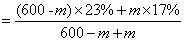
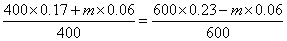
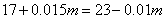
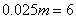
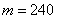 克。再求任何一杯(如甲杯)溶液的浓度:
克。再求任何一杯(如甲杯)溶液的浓度: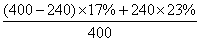
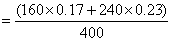
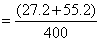
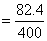
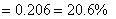 ;所以,选B。考查点:数量关系>数学运算>浓度问题>不同溶液混合
;所以,选B。考查点:数量关系>数学运算>浓度问题>不同溶液混合
47、减数、被减数与差三者之和除以被减数,商是多少_____
A: 0B: 1C: 2D: 减数与差之和
参考答案: C 本题解释: 【解析】C。减数+被减数+差=2被减数,所以商为2。
48、甲、乙两港相距720千米,轮船往返两港需要35小时,逆流航行比顺流航行多花5个小时;帆船在静水中每小时行驶24千米,问帆船往返两港需要多少小时?_____
A: 58B: 60C: 64D: 66
参考答案: C 本题解释:C。分析可知轮船逆流航行了20小时,顺流航行了15小时。可得水流速度是(720÷15—720÷20)÷2=6千米/小时,所以帆船顺水速度是24+6=30千米/小时,逆水速度是24—6=18千米/小时,往返需要720÷30+720÷18=64小时。
49、(2007浙江,第24题)林子里有猴子喜欢吃的野果,23只猴子可以在9周内吃光,21只猴子可以在12周内吃光,问如果有33只猴子-起吃,则需要几周吃光?(假定野果生长的速度不变)_____
A: 2周B: 3周C: 4周D: 5周
参考答案: C 本题解释:参考答案:C题目详解:依题意:设野果的原有存量为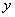 ;单位时间长出量即自然增长量为
;单位时间长出量即自然增长量为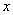 ,存量完全消失所消耗的时间
,存量完全消失所消耗的时间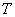 为所求;代入公式:
为所求;代入公式: 所以,选C。考查点:数量关系>数学运算>特殊情境问题>牛儿吃草问题>标准型牛儿吃草问题
所以,选C。考查点:数量关系>数学运算>特殊情境问题>牛儿吃草问题>标准型牛儿吃草问题
50、一百张牌抽掉奇数牌,然后再抽掉剩下牌中位于奇数位的牌……如此最后剩下的一张是原来100张牌排序中的第几张呢?_____
A: 63 B: 64 C: 65 D: 66
参考答案: B 本题解释:B
51、用直线切割一个有限平面,后一条直线与此前每条直线都要产生新的交点,第1条直线将平面分成2块,第2条直线将平面分成4块。第3条直线将平面分成7块,按此规律将平面分为22块需_____。
A: 如果A、B、P不在同一条直线上,汽车所在位置有3个,可位于A、B两地之间或A、B两地外侧B: 如果A、B、P不在同一条直线上,汽车的位置有无穷多个C: 如果A、B、P位于同一条直线上,汽车拉于A、B两地之间或两地外侧D: 如果A、B、P位于同一条直线上,汽车位于A、B两地外侧,且汽车到A的距离为20千米
参考答案: D 本题解释:正确答案是B考点几何问题解析AB距离为40,AP和BP距离之和为60千米,若A、B、P三点在同一直线上,则P点位于AB外侧10千米处;若A、B、P三点不在同一直线上,则转化为A、B点固定,AP+BP=60即可,有无数种选择。故答案为B。
52、某公司计划采购一批电脑,正好赶上促销期,电脑打9折出售,同样的预算可以比平时多买10台电脑。问该公司的预算在平时能多买多少台电脑?_____
A: 60.B: 70C: 80D: 90
参考答案: D 本题解释:【答案】D。解析:设平时可以购买x台,电脑打折前价格为100,则打折后为90,依题意100x=90(x+10),解得=90。
53、(2008安徽)用两根同样长度的铁丝分别圈成圆形和正方形,圆形面积大约是正方形面积的几倍?_____
A: 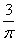 B:
B: 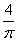 C:
C: 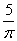 D:
D: 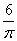
参考答案: B 本题解释:参考答案:B题目详解:依题意:假设圆的半径为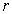 ,正方形的边长为
,正方形的边长为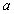 ;由于周长相同(同样长度的铁丝):
;由于周长相同(同样长度的铁丝):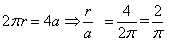 。其面积比应该为:
。其面积比应该为: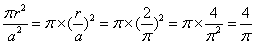 ;所以,选B。考查点:数量关系>数学运算>几何问题>平面几何问题>周长与面积相关问题
;所以,选B。考查点:数量关系>数学运算>几何问题>平面几何问题>周长与面积相关问题
54、某河段中的沉积河沙可供80人连续开采6个月或60人连续开采10个月。如果要保证该河段河沙不被开采枯竭,问最多可供多少人进行连续不间断的开采?(假定该河段河沙沉积的速度相对稳定)_____
A: 25B: 30C: 35D: 40
参考答案: B 本题解释:正确答案是B考点牛吃草问题解析设河沙初始量为M,每月沉积量为N。则有:M=(80-N)×6=(60-N)×10,解得N=30,即每个月的沉积量可供30人开采;可知当开采人数为30时,才能保证连续不间断的开采,故正确答案为B。
55、(2009江苏)如下图,将一个表面积为36平方米的正方体等分成两个长方体,再将这两个长方体拼成一个大长方体,则大长方体的表面积是_____。 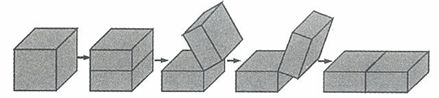
A: 24平方米B: 30平方米C: 36平方米D: 42平方米
参考答案: D 本题解释:参考答案 题目详解:解法一:已知原来正方体每个面的面积都是6平方米,这个过程中,先产生了一个截面,新增了两个平面的面积,即增加了12平方米;原来在右边的那个面在接触过程中被遮住了,不再是表面,即减少了一个平面的面积,即减少了6平方米。综上,大长方体的表面积为
题目详解:解法一:已知原来正方体每个面的面积都是6平方米,这个过程中,先产生了一个截面,新增了两个平面的面积,即增加了12平方米;原来在右边的那个面在接触过程中被遮住了,不再是表面,即减少了一个平面的面积,即减少了6平方米。综上,大长方体的表面积为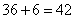 平方米。所以,选D。解法二:同样体积的图形当中,越接近于球,表面积越小,所以正方体变成长方体之后,表面积肯定会增加,由此可以直接判断D为正确答案。考查点:数量关系>数学运算>几何问题>立体几何问题>表面积与体积问题
平方米。所以,选D。解法二:同样体积的图形当中,越接近于球,表面积越小,所以正方体变成长方体之后,表面积肯定会增加,由此可以直接判断D为正确答案。考查点:数量关系>数学运算>几何问题>立体几何问题>表面积与体积问题
56、甲公司的一分厂制造了10台机床,二分厂制造了8台。乙公司向甲公司购买6台机床,丙公司向甲公司购买12台机床。每台机床的运费因运输距离的不同而有差异,具体情况如下表所示。乙、丙两公司购买机床的运费总和最低为_____元。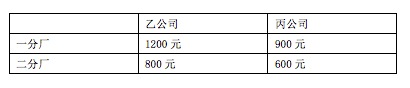
A: 12000B: 13500C: 15000D: 16000
参考答案: C 本题解释:正确答案是C考点统筹规划问题解析乙、丙公司从一分厂购买机床的价格分别为1200、900元,乙、丙公司从二分厂购买机床的价格分别为800、600元,乙、丙公司在一、二分厂的购买价格相差400、300元,为了使乙、丙两个公司的运费最低,二分厂的的机床都应该运至乙公司,乙丙最低运费为:6×800+2×600+(12-2)×900=4800+1200+9000=15000(乙公司买二分厂的6台机床,丙公司购买二分厂过剩余的2台机床和一分厂的10台机床),故购买机床的最低运费为15000元。故正确答案为C。
57、如下图所示,AB两点是圆形体育场直径的两端,两人从AB点同时出发,沿环形跑道相向匀速而行,他们在距A点弧形距离80米处的C点第一次相遇,接着又在距B点弧形距离60米处的D点第二次相遇,问这个圆形体育场的周长是多少米?_____
A: 240B: 300C: 360D: 420
参考答案: C 本题解释:正确答案是C考点行程问题解析解析1:根据题意可知两人第一个运动过程的路程和为半个圆周,第二个运动过程的路程和为整个圆周,因此每个人在两个过程中的路程比为1:2,设劣弧BC长为x,根据题意可得,80:(x+60)=1:2,解得x=100,因此圆周长为:2×(80+100)=360,故正确答案为C。解析2:此题为两次相遇问题,运用公式可得圆周长的一半为:80×3-60=180米,因此周长为360米,故正确答案为C。备注:两次相遇问题,两边型的两端点之间的距离公式:S=3A-B,其中S表示两端点之间的距离,A、B表示先后两次相遇点分别关于两个端点的距离。
58、有两个三口之家一起出行去旅游,他们被安排坐在两排相对的座位上,其中一排有3个座位,另一排有4个座位。如果同一个家庭成员只能被安排在同一排座位相邻而坐,那么共有多少种不同的安排方法?_____
A: 36B: 72C: 144D: 288
参考答案: C 本题解释:正确答案是C考点排列组合问题解析
59、甲、乙两人沿直线从A地步行至B地,丙从B地步行至A地。已知甲、乙、丙三人同时出发,甲和丙相遇后5分钟,乙与丙相遇。如果甲、乙、丙三人的速度分别为85米/分钟、75米/分钟、65米/分钟。问A、B两地距离为多少米?_____
A: 8000米B: 8500米C: 10000米D: 10500米
参考答案: D 本题解释:正确答案是D考点行程问题解析本题理解的重点在于:在甲和丙相遇时,甲比乙多走的距离为后来乙丙一起走的距离。有了这个思想,就容易解出,甲和丙相遇时,甲比乙多走的距离为(75+65)×5=700m,假设甲和丙相遇的时候,甲走了a分钟,则(85-75)a=700,解得a=70。所以两地相距为(85+65)×70=10500米,故正确答案为D。
60、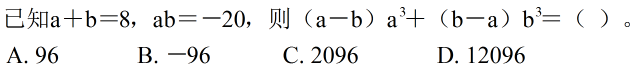 _____
_____
A: AB: BC: CD: D
参考答案: D 本题解释:正确答案是D考点计算问题解析解析1: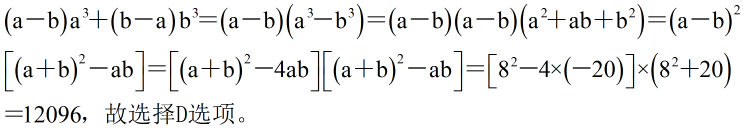
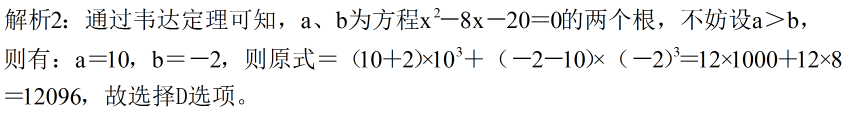 标签完全平方和差公式立方和差公式韦达定理
标签完全平方和差公式立方和差公式韦达定理
61、把一个长18米、宽6米、高4米的大教室,用厚度为25厘米的隔墙将长分为3段,形成3个活动室(隔墙砌到顶),每间活动室的门窗面积都是15平方米,现在用石灰粉刷3个活动室的内墙壁和天花板,平均每平方米用石灰0.2千克,那么,一共需要石灰_____千克。
A: 68.8B: 74.2C: 83.7D: 59.6
参考答案: A 本题解释:参考答案:A题目详解:根据题意,可知:天花板总面积是:(18-0.25×2)×6=105平方米,内壁总面积是:(18-0.25×2)×4×2+4×6×6-15×3=239平方米,需用石灰粉刷的总面积是:105+239=344平方米,需用石灰为:344×0.2=68.8千克。考查点:数量关系>数学运算>几何问题>立体几何问题>表面积与体积问题
62、有a、b、c、d四条直线,依次在a线上写1,在b线上写2,在c线上写3,在d线上写4,然后在a线上写5,在b线、c线和d线上写数字6,7,8…按这样的周期循环下去,问数字2007在哪条线上?_____
A: a线B: b线C: c线D: d线
参考答案: C 本题解释:正确答案是C考点周期问题解析该循环以4为周期,2007÷4=501余3,那么2007应该标在c线上,故正确答案为C
63、6个空瓶可以换一瓶汽水,某班同学喝了157瓶汽水,其中有一些是用喝剩下来的空瓶换的,那么他们至少要买多少瓶汽水?_____
A: 131 B: 130 C: 128 D: 127
参考答案: A 本题解释: 【解析】A。131÷5×6=157.2(取整)=157。
64、有一路电车从甲站开往乙站,每五分钟发一趟,全程走15分钟。有一人从乙站骑自行车沿电车线路去甲站。出发时,恰好有一辆电车到达乙站,在路上他又遇到10辆迎面开来的电车,到站时恰好有一辆电车从甲站开出,那么,他从乙站到甲站共用多少分钟?_____
A: 40B: 6C: 48D: 45
参考答案: A 本题解释:正确答案是A考点行程问题解析当编号为A1的第一辆车到达乙站时,编号为A4的第四辆车恰好刚从甲站出发,假设骑车人刚从乙站出发时,编号为A1的第一辆车到达乙站,则途中骑车人又遇到了10辆车,则当他到达甲站时,恰好编号为A12的第十二辆车从甲站开出,而此时编号为A9的第九辆车刚刚到达乙站,显然,电车从A1到A9所用的时间也恰是骑车人用的时间,所以答案为(9-1)×5=40分钟。正确答案选A。
65、为节约用水,某市决定用水收费实行超额超收,标准用水量以内每吨2.5元,超过标准的部分加倍收费。某用户某月用水15吨,交水费62.5元,若该用户下个月用水12吨,则应交水费多少钱?_____
A: 42.5元B: 47.5元C: 50元D: 55元
参考答案: B 本题解释:正确答案是B考点鸡兔同笼问题解析解析1:先将15吨全部看成超出的部分,则按照每吨5元收费,共计收费75元,而实际交水费62.5元,少交12.5元。这是因为标准量以内每吨2.5元,比整体看做超出部分计价少交2.5元,因此标准用水量为5吨。因此12吨应交水费为5×2.5+7×5=47.5元。故正确答案为B。解析2:设标准用水量上限为A吨,则有2.5A+5×(15-A)=62.5,解得A=5。用水12吨,应交水费2.5×5+5×(12-5)=47.5元。故正确答案为B。秒杀技将12吨用水看成标准量以内,应交水费为12×2.5=30元,但四个选项中没有此值,这说明12吨是超过标准用水量。那么15吨必然也是超过标准用水量,要计算12吨应交的水费,只需从15吨所交62.5元中扣除多超出的3吨的价钱即15元即可,也即为47.5元。故正确答案为B。标签差异分析
66、小明和小方各走一段路,小明走的路程比小方多1/5,小方用的时间比小明多1/8。小明和小方的速度之比是多少?_____
A: 37∶14B: 27∶20C: 24∶9D: 21∶4
参考答案: B 本题解释: B【解析】依题意,小明与小芳路程的比是(1+1/5):1=6:5小明与小芳时间的比是1:(1+1/8)=8:9小明与小芳速度的比是:6/8:5/9=27:20。
67、(2009江苏A类)对正实数定义运算,若 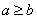 ,则
,则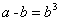 ; 若
; 若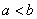 ,则
,则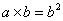 。由此可知,方程
。由此可知,方程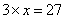 的解是:_____ B: 9C:
的解是:_____ B: 9C: 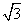 D: 3,
D: 3,
参考答案: D 本题解释:参考答案 题目详解:根据题意可知,若
题目详解:根据题意可知,若 ,则
,则 ,即
,即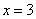 ;若
;若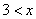 ,则
,则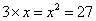 ,即只能有
,即只能有 。因此,选D。考查点:数量关系>数学运算>计算问题之算式计算>定义新运算问题
。因此,选D。考查点:数量关系>数学运算>计算问题之算式计算>定义新运算问题
68、某天办公桌上台历显示的是一周前的日期,将台历的日期翻到今天,正好所翻页的日期加起来是168,那么今天是几号?_____
A: 20B: 21C: 27D: 28
参考答案: D 本题解释:正确答案是D考点数列问题解析一周的日期成等差数列,则中位数为168÷7=24,因此这一周的日期分别为21、22、23、24、25、26、27,因此今天是28号。故正确答案为D。
69、某次考试100道选择题,每做对一题得1.5分,不做或做错一题扣1分,小李共得100分,那么他答错多少题_____
A: 20B: 25C: 30D: 80
参考答案: A 本题解释:A【解析】不做或做错的题目为(100×1.5-100)÷(1.5+1)=20。
70、100个自然数的和是20000,其中奇数的个数比偶数的个数多,那么偶数最多能有多少个?_____
A: 38B: 40C: 48D: 49
参考答案: C 本题解释:参考答案:C题目详解:依题意:“100个自然数的和是20000”,即和为偶数;又因为奇数的个数为偶数个,奇数的个数比偶数的个数多:所以最多有100÷2-2=48个偶数;所以,选C。考查点:数量关系>数学运算>计算问题之数的性质>奇偶性与质合性问题>奇偶性
71、五个瓶子都贴有标签,其中恰好贴错了三个,贴错的可能情况有多少种?_____
A: 60B: 46C: 40D: 20
参考答案: D 本题解释:D【解析】根据题意贴错三个,贴对两个。首先从五个瓶子中选出3个的种类为C35=10种,这三个瓶子为贴错标签的,这三个瓶子贴错标签的有两种情况。所以五个瓶子中贴错三个标签的情况有10×2=20种。
72、甲、乙两仓库各放有集装箱若干个,第一天从甲仓库移出和乙仓库集装箱总数同样多的集装箱到乙仓库,第二天从乙仓库移出和甲仓库集装箱总数同样多的集装箱到甲仓库,如此循环,则到第四天后,甲乙两仓库集装箱总数都是48个,问甲仓库原来有多少个集装箱?_____
A: 33B: 36C: 60D: 63
参考答案: D 本题解释:正确答案是D考点趣味数学问题解析逆向考虑即可,从第四天起向前逆推,甲48、乙48→甲24、乙72→甲60、乙36→甲30、乙66→甲63、乙33(此为第一天移动前),则甲仓库原来有63个集装箱。故正确答案为D。秒杀技根据题意可知甲仓库显然比乙仓库多,否则不能相互搬运,故排除A、B;代入60,第一次搬运:甲24、乙72,第二次搬运:甲48、乙48,显然不符合题意,排除C。故正确答案为D。
73、173×173×173-162×162×162=_____
A: 926183B: 936185C: 926187D: 926189
参考答案: D 本题解释:正确答案是D考点计算问题解析根据尾数法,173×173×173尾数为7,162×162×162尾数为8,因此173×173×173-162×162×162尾数为9,故正确答案为D。
74、某市出租车运费计算方式如下:起步价2公里6元,2公里之后每增加1公里收费1.7元,6公里之后每增加1公里收费2.0元,不足1元按四舍五入计算。某乘客乘坐了31公里,应该付多少元车费? _____
A: 63 B: 64 C: 65 D: 66
参考答案: A 本题解释:A。2公里以内收费6元;2-6公里收费1.7×4=6.8元;6-31公里收费2×25=50元。因此总计应付车费62.8元,四舍五入即63元。故选A项。
75、自然数P满足下列条件:P除以10的余数为9,P除以9的余数为8,P除以8的余数为7。如果:100<P<1000,则这样的P有几个?_____
A: 不存在B: 1个C: 2个D: 3个
参考答案: C 本题解释:正确答案是C解析由" 除以10的余数为9,P除以9的余数为8,P除以8的余数为7",满足差同减差,对应口诀可知其符合表达式为360n-1,由于100<P<1000,则100<360n-1<1000,所以n能取1、2,则满足条件的P有两个,即359和719,故正确答案为C。注释:同余问题需要掌握如下口诀:余同取余,和同加和,差同加差,最小公倍数做周期。口诀解释:余同取余,例如"一个数除以7余1,除以6余1,除以5余1",可见所得余数恒为1,则取1,被除数的表达式为210n+1;和同加和,例如"一个数除以7余1,除以6余2,除以5余3",可见除数与余的和相同,取此和8,被除数的表达式为210n+8;差同减差,例如"一个数除以7余3,除以6余2,除以5余1",可见除数与余的差相同,取此差4,被除数的表达式为210n-4。特别注意前面的210是5、6、7的最小公倍数。余数与同余问题标签同余问题
除以10的余数为9,P除以9的余数为8,P除以8的余数为7",满足差同减差,对应口诀可知其符合表达式为360n-1,由于100<P<1000,则100<360n-1<1000,所以n能取1、2,则满足条件的P有两个,即359和719,故正确答案为C。注释:同余问题需要掌握如下口诀:余同取余,和同加和,差同加差,最小公倍数做周期。口诀解释:余同取余,例如"一个数除以7余1,除以6余1,除以5余1",可见所得余数恒为1,则取1,被除数的表达式为210n+1;和同加和,例如"一个数除以7余1,除以6余2,除以5余3",可见除数与余的和相同,取此和8,被除数的表达式为210n+8;差同减差,例如"一个数除以7余3,除以6余2,除以5余1",可见除数与余的差相同,取此差4,被除数的表达式为210n-4。特别注意前面的210是5、6、7的最小公倍数。余数与同余问题标签同余问题
76、(2007北京社招,第25题)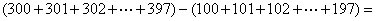 _____。
_____。
A: 19000B: 19200C: 19400D: 19600
参考答案: D 本题解释:参考答案 题目详解:应用凑整法:原式=
题目详解:应用凑整法:原式=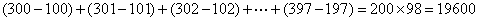 ,所以,选D。考查点:数量关系>数学运算>计算问题之算式计算>速算与技巧>凑整法
,所以,选D。考查点:数量关系>数学运算>计算问题之算式计算>速算与技巧>凑整法
77、甲、乙两时钟都不正确,甲钟每走24小时,恰好快1分钟;乙钟每走24小时,恰好慢1分钟。假定今天下午三点钟的时候,将甲、乙两钟都调好,指在准确的时间上,任其不停地走下去,问下一次这两只钟都同样指在三点时,要隔多少天?_____
A: 30B: 240C: 480D: 720
参考答案: D 本题解释:【答案解析】可以先求出甲钟比标准时钟多转一圈所需天数,标准时钟比乙钟多走一圈所需天数,然后再求二者的最小公倍数。甲钟与标准时钟下一次同时指向三点时,甲钟比标准时钟多转一圈,也就是多走12小时,即60×12分钟,需要60×12÷(61-60)=720÷1=720(天)同样,标准时钟与乙钟下一次同时指向三点时,标准时钟比乙钟多转一圈,需要60×12÷(60-59)=720÷1=720(天)所以,经过720天后,甲、乙两钟同时指在三点。故正确答案为D。
78、草地上插了若干根旗杆,已知旗杆的高度在1至5米之间,且任意两根旗杆的距离都不超过它们高度差的10倍。如果用一根绳子将所有旗杆都围进去,在不知旗杆数量和位置的情况下,最少需要准备多少米长的绳子?_____
A: 40B: 100C: 60D: 80
参考答案: D 本题解释:正确答案是D考点几何问题解析解析1: 解析2:旗杆最高为5米,最矮为1米。因此任意两旗杆间的距离不超过(5-1)×10=40米。以最矮的旗杆为原点,最矮的旗杆与最高的旗杆连线为x轴建立直角坐标系。当这两个旗杆间距最大时,如下左图所示。设其余任意旗杆高度为a。要满足与1米旗杆间距离不超过它们高度差的10倍,应在下图左边的圆范围内。要满足与5米旗杆间距离不超过它们高度差的10倍,应在下图右边的圆范围内。同时满足条件的旗杆只能位于两个旗杆的连线上。此时需要40×2=80米可把它们都围进去。若两个旗杆间距小于40米,如右图所示,其余旗杆应该在两圆相交的阴影范围内分布,此时需要2×[10(a-1)+10(5-a)]=80米。因此不论旗杆怎样分布,都需要至少80米长的绳子来保证把全部旗杆围进去,故正确答案为D。
解析2:旗杆最高为5米,最矮为1米。因此任意两旗杆间的距离不超过(5-1)×10=40米。以最矮的旗杆为原点,最矮的旗杆与最高的旗杆连线为x轴建立直角坐标系。当这两个旗杆间距最大时,如下左图所示。设其余任意旗杆高度为a。要满足与1米旗杆间距离不超过它们高度差的10倍,应在下图左边的圆范围内。要满足与5米旗杆间距离不超过它们高度差的10倍,应在下图右边的圆范围内。同时满足条件的旗杆只能位于两个旗杆的连线上。此时需要40×2=80米可把它们都围进去。若两个旗杆间距小于40米,如右图所示,其余旗杆应该在两圆相交的阴影范围内分布,此时需要2×[10(a-1)+10(5-a)]=80米。因此不论旗杆怎样分布,都需要至少80米长的绳子来保证把全部旗杆围进去,故正确答案为D。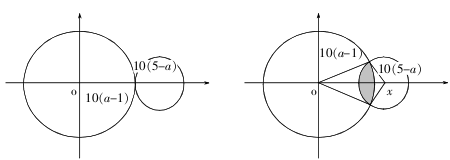 标签画图分析
标签画图分析
79、某宾馆一层客房比二层客房少5间,某旅游团48人,若全安排在第一层,每间4人,房间不够,每间5人,则有房间住不满;若全安排在第二层,每间3人,房间不够,每间住4人,则有房间住不满,该宾馆一层有客房多少间?_____
A: 9B: 10C: 11D: 13
参考答案: B 本题解释:参考答案:B题目详解:设该宾馆一层有客房x间: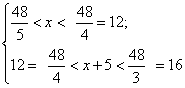 ,所以,
,所以,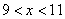 ,因此
,因此 ,即宾馆一层有10间客房。(z为取整)
,即宾馆一层有10间客房。(z为取整)
80、某汽车厂离生产甲、乙、丙三种车型,其中乙型产量的3倍与丙型产量的6倍之和等于甲型产量的4倍,甲型产量与乙型的2倍之和等于丙型产量的7倍。则甲、乙、丙三型产量之比为_____。
A: 5:4:3B: 4:3:2C: 4:2:1D: 3:2:1
参考答案: D 本题解释:正确答案是D考点和差倍比问题解析设甲的产量为x,乙的产量为y,丙的产量为z。则可得如下:3y+6z=4x,x+2y=7z,两式相加可得3x+z=5y,直接带入选项,只有D符合,故正确答案为D。秒杀技得到3y+6z=4x后,观察该式,可知x应为3的倍数,只有D符合。标签直接代入
81、(2008山西)若干学校联合进行团体表演,参演学生组成一个方阵,已知方阵由外到内第二层有104人,则该方阵共有学生_____人。
A: 625B: 841C: 1024D: 1369
参考答案: B 本题解释:参考答案:B题目详解:根据方阵公式:最外层人数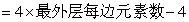 可得:由外到内第二层每排的学生数:
可得:由外到内第二层每排的学生数: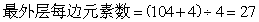 个;最外一层每排有学生有:最外层每边元素数=内层每边元素数+2:
个;最外一层每排有学生有:最外层每边元素数=内层每边元素数+2: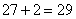 个;所以该方阵共有学生有:
个;所以该方阵共有学生有: 个。所以,选B考查点:数量关系>数学运算>特殊情境问题>方阵问题>实心方阵问题
个。所以,选B考查点:数量关系>数学运算>特殊情境问题>方阵问题>实心方阵问题
82、一个边长为80厘米的正方形,依次连接四边中点得到第二个正方形,这样继续下去可得到第三个、第四个、第五个、第六个正方形,问第六个正方形的面积是多少平方厘米?_____
A: 128平方厘米B: 162平方厘米C: 200平方厘米D: 242平方厘米
参考答案: C 本题解释:正确答案是C考点几何问题解析 秒杀技第一个正方形边长为80厘米,因此其面积值中含有5因子,而每次是变为原来的一半,5因子并未去掉,因此第六个正方形面积值中也含有5因子,四个选项中仅C选项能被5整除,故选择C选项。标签数字特性
秒杀技第一个正方形边长为80厘米,因此其面积值中含有5因子,而每次是变为原来的一半,5因子并未去掉,因此第六个正方形面积值中也含有5因子,四个选项中仅C选项能被5整除,故选择C选项。标签数字特性
83、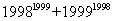 的尾数是_____:
的尾数是_____:
A: 3B: 6C: 7D: 9
参考答案: A 本题解释:参考答案:A题目详解:备注:用户“lumin”(2010-10-0222:00:56),认为:题有问题!正确答案应该是“尾数7”但经过分析,我们认为该题没有问题,答案也不存在歧义考查点:数量关系>数学运算>计算问题之数的性质>数字问题>数字的重新排列
84、从一楼走到五楼,爬完一层休息30秒,一共要210秒,那么从一楼走到7楼,需要多少秒_____
A: 318B: 294C: 330D: 360
参考答案: C 本题解释:C【解析】从一点走到五楼,休息了三次,那么每爬上一次需要的时间为(210-30×3)÷(5-1)=30秒,故从一楼走到七楼需要30×(7-1)+30×(7-2)=330秒。
85、某单位招待所有若干间房间,现要安排一支考察队的队员住宿,若每问住3人,则有2人无房可住;若每问住4人,则有一间房间不空也不满,则该招待所的房间最多有_____。
A: 5间B: 4间C: 6间D: 7间
参考答案: A 本题解释:A。
86、甲、乙两辆清洁车执行东、西城间的公路清扫任务。甲车单独清扫需要6小时,乙车单独清扫需要9小时,两车同时从东、西城相向开出,相遇时甲车比乙车多清扫15千米。问东、西两城城相距多少千米?_____
A: 60B: 75C: 90D: 135
参考答案: B 本题解释: 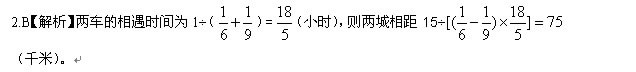
87、甲、乙两辆清洁车执行东、西城间的公路清扫任务。甲车单独清扫需要6小时,乙车单独清扫需要9小时,两车同时从东、西城相向开出,相遇时甲车比乙车多清扫15千米。问东、西两城相距多少千米?_____
A: 60千米B: 75千米C: 90千米D: 135千米
参考答案: B 本题解释:正确答案是B考点工程问题解析甲乙的速度比为3:2,设全程为5份,则甲乙相遇时甲清扫了3份,乙清扫了2份,甲比乙多1份,而1份对应15千米,因此东西两城相距5×15=75千米。标签赋值思想比例转化
88、假设五个相异正整数的平均数是15,中位数是18,则此五个正整数中的最大数的最大值可能为_____。
A: 24B: 32C: 35D: 40
参考答案: C 本题解释:参考答案:C题目详解:根据题意:5个数的平均数为15;那么这5个数的和为: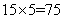 。要使最大数尽量大,那么必须使小的数尽量小;设小的两个数为1和2:又因为中位数是18,那么较大的两个数之和为:
。要使最大数尽量大,那么必须使小的数尽量小;设小的两个数为1和2:又因为中位数是18,那么较大的两个数之和为: ;而这两个数都大于18,所以要使最大的数尽量大:那么使第二大的数为19,所以最大的数为
;而这两个数都大于18,所以要使最大的数尽量大:那么使第二大的数为19,所以最大的数为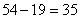 。所以,选C。考查点:数量关系>数学运算>计算问题之算式计算>平均值问题>算术平均值
。所以,选C。考查点:数量关系>数学运算>计算问题之算式计算>平均值问题>算术平均值
89、小李开了一个多小时会议,会议开始时看了手表,会议结束时又看了手表,发现时针与分针恰好互换了位置。问这次会议大约开了1小时多少分?_____
A: 51B: 47C: 45D: 43
参考答案: A 本题解释:A。时针和分针正好互换了位置,说明两针一共转了720度。因为时针每分钟转过0.5度,分针每分钟转过6度,所以720÷(6+0.5)≈110.7分,约为l小时51分。
90、有一段阶梯,如果每步跨4级,最后会剩下2级,如果每步跨5级,最后则会剩下1级。已知这段阶梯的级数可以被3整除,则这段阶梯共有_____级。
A: 42B: 46C: 63D: 66
参考答案: D 本题解释:参考答案:D题目详解:设阶梯共有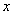 级:
级: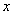 除以4余2,除以5余l,根据同余问题"和同加和,最小公倍数做周期"可知:
除以4余2,除以5余l,根据同余问题"和同加和,最小公倍数做周期"可知: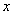 可以表示为
可以表示为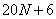 ;B、D均符合。又因为阶梯的级数可以被3整除:所以排除B项;所以,选D。考查点:数量关系>数学运算>计算问题之数的性质>余数问题>一个被除数,多个除数>特殊形式>和同
;B、D均符合。又因为阶梯的级数可以被3整除:所以排除B项;所以,选D。考查点:数量关系>数学运算>计算问题之数的性质>余数问题>一个被除数,多个除数>特殊形式>和同
91、一个长方形,它的周长是32米,长是宽的3倍。这个长方形的面积是多少平方米?_____
A: 64B: 56C: 52D: 48
参考答案: D 本题解释:D设宽为x则长为3x,则2(x+3x)=32,则x=4,故面积为48平方米。
92、正方体 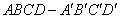 中,侧面对角线
中,侧面对角线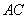 与
与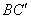 所成的角等于_____。
所成的角等于_____。 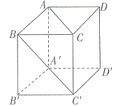
A: 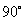 B:
B: 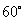 C:
C: 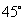 D:
D: 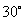
参考答案: B 本题解释:参考答案:B题目详解:根据题意, 连接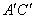 与
与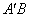 。∵
。∵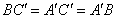 ∴
∴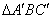 为等边三角形,又∵
为等边三角形,又∵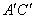 与
与 平行,∴侧面对角线
平行,∴侧面对角线 与
与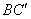 所成的角等于
所成的角等于 。因此,选B。考查点:数量关系>数学运算>几何问题>立体几何问题>与线、角相关问题(立体)
。因此,选B。考查点:数量关系>数学运算>几何问题>立体几何问题>与线、角相关问题(立体)
93、小张在做一道除法时,误将除数45看成54,结果得到的商是3,余数是7。问正确的商和余数之和是_____。
A: 11B: 18C: 26D: 37
参考答案: D 本题解释:正确答案是D考点余数与同余问题解析由题意,被除数=54×3+7=169,于是正确的除法过程为169÷45=3••••••34,正确的商与余数之和为37。故正确答案为D。
94、一个容器内有若干克盐水。往容器内加入一些水,溶液的浓度变为3%,再加入同样多的水,溶液的浓度变为2%,问第三次再加入同样多的水后,溶液的浓度是_____。
A: 1.8%B: 1.5%C: 1%D: 0.5%
参考答案: B 本题解释:正确答案是B考点浓度问题解析设浓度为3%的溶液有100克,加入x克水后浓度变为2%,加水前后溶液中的盐的质量是不变的,所以可列方程:100×3%=(100+x)×2%,解得x=50克,第三次加入50克水后,溶液的浓度为(100×3%)÷(100+50+50)=1.5%,故正确答案为B。
95、某单位2011年招聘了65名毕业生,拟分配到该单位的7个不同部门,假设行政部门分得的毕业生人数比其他部门都多,问行政部门分得的毕业生人数至少为多少名?_____
A: 10B: 11C: 12D: 13
参考答案: B 本题解释:正确答案是B考点趣味数学问题解析65÷7=9余2,即平均分配给7个不同部门还剩余2名毕业生,已知行政部门毕业生毕业生最多,所以只需将剩余的2名毕业生分配给行政部门即可(如果只分配1名,那么其他部门也会出现不少于10人的情况),可得9+2=11,故正确答案为B。
96、2006×20072007-2007×20062006的值为_____。
A: ﹣10C: 100D: 1000
参考答案: B 本题解释:正确答案是B考点多位数问题解析原式=2006×(20070000+2007)-2007×(20060000+2006)=2006×2007×10000+2006×2007-2007×2006×10000-2007×2006=0,故正确答案为B。
97、某校下午2点整派车去某厂接劳模作报告,往返须1小时。该劳模在下午1点整就离厂步行向学校走来,途中遇到接他的车,便坐上车去学校,于下午2点40分到达。问汽车的速度是劳模的步行速度的几倍? _____
A: 4B: 6C: 7D: 8
参考答案: D 本题解释:D。【解析】本题要画图辅助,假设全程距离为1,汽车来回的时间为1小时,所以,其速度为1,汽车运行时间为2/3小时,所以汽车跑的路程为2/3,人走的距离为剩下1/3路程的一半,即1/6,步行的时间为1小时20分,所以步行的速度是1/6÷(1+1/3)=1/8,所以汽车的速度是劳模的8倍。选D。
98、加工一批零件,甲独做需3天完成,乙独做需4天完成,两人同时加工,完成任务时,甲比乙多做24个,这批零件有多少个?_____
A: 168B: 154C: 196D: 336
参考答案: A 本题解释:正确答案是A考点工程问题解析解析1:设这批零件共12份,则甲一天完成4份,乙一天完成3份。甲、乙同时加工需12÷(4+3)=12/7天,甲比乙多做了(4-3)×12/7=12/7份,24个,则每份有24÷12/7=14个,这批零件共有12×14=168个。故正确答案为A。解析2:甲、乙两人同时加工需1÷(1/3+1/4)=12/7天。设这批零件共y个,由题意得(y/3-y/4)×12/7=24,解得y=168,故正确答案为A。标签赋值思想
99、河道赛道长120米,水流速度为2米/秒,甲船速度为6米/秒,乙船速度为4米/秒。比赛进行两次往返,甲、乙同时从起点出发,先顺水航行,问多少秒后甲、乙船第二次迎面相遇?_____
A: 48 B: 50 C: 52 D: 54
参考答案: C 本题解释: C。
100、如右图所示,△ABC是等腰直角三角形,AB=12,AD的长度是CD的2倍,四边形EBCD与△AED的面积之比为3:2,AE的长度是_____。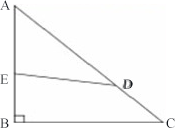
A: 6.9B: 7.1C: 7.2D: 7.4
参考答案: C 本题解释:正确答案是C考点几何问题解析四边形EBCD与三角形AED的面积之比为3:2,则三角形ABC与三角形AED的面积之比为5:2。已知AD的长度是CD的2倍,则AD的长度是AC的2/3。作DF垂直AB于点F,则DF=2/3BC(相似三角形原理),三角形ABC的面积=1/2×AB×BC,三角形AED的面积=1/2×AE×DF=1/2×AE×2/3BC代入之前的比例式,可得AE=3/5AB=36/5=7.2。所以正确答案为C。