微信搜索关注"91考试网"公众号,领30元,获取公务员、事业编、教师等考试资料40G!
1、一个边长为20的方阵,最外面三圈人数总和为多少?_____
A: 196B: 204C: 256D: 324
参考答案: B 本题解释:参考答案:B题目详解:方阵边长为20,总人数为400;除去最外面三圈人数,里面的小方阵边长为: ,人数为
,人数为 ;最外面三圈人数为:
;最外面三圈人数为: 人。所以,选B。考查点:数量关系>数学运算>特殊情境问题>方阵问题>空心方阵问题
人。所以,选B。考查点:数量关系>数学运算>特殊情境问题>方阵问题>空心方阵问题
2、某单位今年一月份购买5包A4纸、6包B5纸,购买A4纸的钱比B5纸少5元;第一季度该单位共购买A4纸15包、B5纸12包、共花费510元;那么每包B5纸的价格比A4纸便宜_____。
A: 1.5元B: 2.0元C: 2.5元D: 3.0元
参考答案: C 本题解释:C【解析】方程问题。设A4纸和B5纸的价格分别为x元和y元。由题意可得方程,6y-5x=5,15x+12y=510解得x=20,y=17.5,所以每包纸比A4纸便宜20-17.5=2.5元。答案选择C选项。
3、某商场促销,晚上八点以后全场商品在原来折扣基础上再打9.5折,付款时满400元再减100元,已知某鞋柜全场8.5折,某人晚上九点多去该鞋柜买了一双鞋,花了384.5元,问这双鞋的原价为多少元钱? _____
A: 550B: 600C: 650D: 700
参考答案: B 本题解释:【答案】B。解析:若付款时不满400元,则原价为384.5÷95%÷85%元,结果为非整数,没有选项符合;若付款时满400元,则原价为(384.5+100)÷95%÷85%=600元,选择B。
4、从0、1、2、4、7五个数中选出三个组成三位数,其中能被3整除的最大数和能被5整除的最小数之差为:_____
A: 618B: 621C: 649D: 729
参考答案: B 本题解释:参考答案:B题目详解:能被3整除的数,且是最大数:满足百位和十位的数字尽可能的大,且与个位数字之和为3的倍数;因此,组成的能被3整除的最大整数为741。能被5整除的数,且是最小数:满足百位和十位的数字尽可能的小,且末位数字是0或5;因此,组成的能被5整除的最小数为120。根据题意,求得最大数与最小数的差:741-120=621;因此,选B。考查点:数量关系 > 数学运算 > 计算问题之数的性质 > 整除问题 > 整除特征
5、一间长250米、宽10米、高4米的仓库放置了1000个棱长为1米的正方体箱子,剩余的空间是多少立方米?_____ B: 1500C: 5000D: 9000
参考答案: D 本题解释:D。【解析】进行简单的数字计算即可,250×10×4-1000×1=9000(m3)。
6、如图,已知直角梯形ABCD的上底长18厘米,下底长27厘米,高24厘米,三角形ABF、三角形ADE和四边形AECF’面积相等。三角形AEF的面积为多少平方厘米?_____ 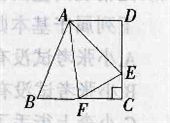
A: 165B: 132C: 160D: 156
参考答案: D 本题解释:参考答案 题目详解:依题意:
题目详解:依题意: 平方厘米;且
平方厘米;且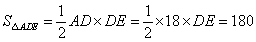 平方厘米;故
平方厘米;故 厘米;则
厘米;则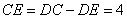 厘米;
厘米; 方厘米;故
方厘米;故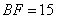 厘米,
厘米,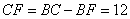 厘米,
厘米,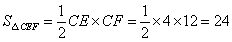 平方厘米;
平方厘米;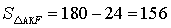 平方厘米;所以,选D。考查点:数量关系>数学运算>几何问题>平面几何问题>周长与面积相关问题
平方厘米;所以,选D。考查点:数量关系>数学运算>几何问题>平面几何问题>周长与面积相关问题
7、甲、乙、丙三人买书共花费96元钱,已知丙比甲多花16元,乙比甲多花8元,则甲、乙、丙三人花的钱的比是_____。
A: 3:5:4B: 4:5:6C: 2:3:4D: 3:4:5
参考答案: D 本题解释:D【解析】设甲花的钱为x,则x+(x+16)+(x+8)=96,则x=24。故三人花的钱的比为24:32:40=3:4:5。
8、用两根同样长度的铁丝分别圈成圆形和正方形,圆形面积大约是正方形面积的几倍?_____
A: 3/πB: 4/πC: 5/πD: 6/π
参考答案: B 本题解释:B解析:正方形周长=4a=xa=x/4圆的周长=2πr=xr=x/2π正方形面积=aa=xx/16圆的面积=πrr=πxx/4ππ=xx/4π,圆的面积是正方形面积的(xx/4π)/(xx/16)=4/π=1.27,选B。
9、某人上午8点要上班,可是发现家里的闹钟停在了6点10分,他上足发条但忘了对表就急急忙忙的上班去了,到公司一看还提前了10分钟。中午12点下班后,回到家一看,闹钟才11点整,假定此人上班、下班在路上用的时间相同,那么他家的闹钟停了多少分钟?_____
A: 100B: 90C: 80D: 70
参考答案: C 本题解释:【解析】C。由题意知:6时10分+闹钟停的时间=7时50分;11时+闹钟停的时间=12时+下班后路上走的时间,所以闹钟停的时间+上班时间=7时50分-6时10分=100分钟,闹钟停的时间上班时间=12时-11时=60分,故闹钟停的时间为(100+60)÷2=80分钟。
10、某市为合理用电,鼓励各用户安装峰谷电表,市原电价每度0.53元,改新表后,每晚10点至次日早8点为低谷,每度收0.28元,其余时间为高峰期,每度0.56元,为改装新电表每个用户须收取100元改装费,假定某用户每月用200度电,两个不同时段用电量各为100度,那么改装电表12个月后,该用户可节约_____元。
A: 161B: 162C: 163D: 164
参考答案: D 本题解释:正确答案是D考点经济利润问题解析电表改装之前该用户每年的用电费用为200×0.53×12=1272元;改装电表之后,该用户这一年的用电费用加上改装费用共(0.28×100+0.56×100)×12+100=1108元,该用户改装电表前后可节约1272-1108=164元。故正确答案为D。
11、一个人到书店购买了一本书和一本杂志,在付钱时,他把书的定价中的个位上的数字和十位上的看反了,准备付21元取货。售货员说:“您应该付39元才对。”请问书比杂志贵多少钱?_____
A: 20B: 21C: 23D: 24
参考答案: C 本题解释:参考答案:C题目详解:解法一:将选项一一代入题目进行验证:看错价钱后,书的价格比原来的价格少了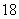 元;所以,看错定价后的书价为13元时符合题目的要求。则书的定价为31元,由于看错后准备付21元:所以杂志的定价为
元;所以,看错定价后的书价为13元时符合题目的要求。则书的定价为31元,由于看错后准备付21元:所以杂志的定价为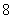 元,书比杂志贵
元,书比杂志贵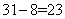 元。所以,选C。解法二:列方程法:根据题意可知:顾客少付39-21=18元。设书的价钱为l0x+y:则将价钱看错后需付款10y+x(此时y处于十位,有y>0),二者之差为9(x-y)=18,因此有x-y=2。由于十位与各位相差2:所以书价格有可能是31,42…因为总价是39,即x=3,y=1;所以书价只能是31元。而杂志的定价为8元,书比杂志贵31-8=23元。所以,选C。考查点:数量关系>数学运算>计算问题之数的性质>数字问题>数字的拆分
元。所以,选C。解法二:列方程法:根据题意可知:顾客少付39-21=18元。设书的价钱为l0x+y:则将价钱看错后需付款10y+x(此时y处于十位,有y>0),二者之差为9(x-y)=18,因此有x-y=2。由于十位与各位相差2:所以书价格有可能是31,42…因为总价是39,即x=3,y=1;所以书价只能是31元。而杂志的定价为8元,书比杂志贵31-8=23元。所以,选C。考查点:数量关系>数学运算>计算问题之数的性质>数字问题>数字的拆分
12、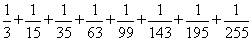 的值是_____
的值是_____
A: 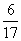 B:
B: 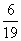 C:
C: 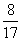 D:
D: 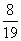
参考答案: C 本题解释:参考答案:C题目详解:本题可以拆项化简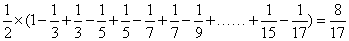 ,选择C。考查点:数量关系>数学运算>计算问题之算式计算>数列问题>数列求和>单一数列求和>分式数列求和
,选择C。考查点:数量关系>数学运算>计算问题之算式计算>数列问题>数列求和>单一数列求和>分式数列求和
13、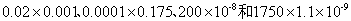 哪个最小?_____
哪个最小?_____
A: 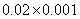 B:
B: 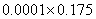 C:
C: 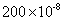 D:
D: 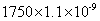
参考答案: D 本题解释:参考答案 题目详解:四个式子分别用科学计数法表示为:
题目详解:四个式子分别用科学计数法表示为: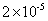 ,
,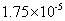 ,
,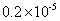 ,
,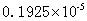 ;则最小的为
;则最小的为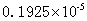 ,即最小的式子为
,即最小的式子为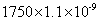 。所以,选D。考查点:数量关系>数学运算>计算问题之算式计算>比较大小问题
。所以,选D。考查点:数量关系>数学运算>计算问题之算式计算>比较大小问题
14、2004×(2.3×47+2.4)÷(2.4×47-2.3)的值为_____。
A: 2003B: 2004C: 2005D: 2006
参考答案: B 本题解释:答案:B
15、某路公交车单程共有10个车站,从始发站出发时,车上共有乘客20人,之后中间每站新上5人,且车上所有乘客最多做3站下车。问最多会有多少名乘客在终点站下车?_____
A: 20B: 10C: 5D: 15
参考答案: D 本题解释:正确答案是D考点趣味数学问题解析由题意,最初的20人在第4站都要下车;每一站新上的人都在3站后下车,那么只有第7站及以后的人才可能在终点站下车。也就是说最多有第7站、第8站、第9站的新上的人在终点站下车,因此最多有15人在终点站下车,正确答案为D。
16、有十名学生参加某次数学竞赛,已知前八名的平均成绩是90分,第九名比第十名多2分,所有学生的平均成绩是87分。问第九名学生的数学成绩是几分?_____
A: 70B: 72C: 74D: 76
参考答案: D 本题解释:正确答案是D解析第九名和第十名的成绩和为87×10-90×8=150,第九名比第十名多2分,所以第九名的分数=(150+2)÷2=76(分),故正确答案为D。平均数问题
17、(2008广西,第12题)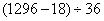 的值是_____。
的值是_____。
A: 20B: 35.5C: 19D: 36
参考答案: B 本题解释:参考答案:B题目详解:应用首尾数法: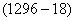 的尾数为8,尾数为8的数除以36尾数明显不可能是整数;所以,选B。考查点:数量关系>数学运算>计算问题之算式计算>速算与技巧>首尾数法
的尾数为8,尾数为8的数除以36尾数明显不可能是整数;所以,选B。考查点:数量关系>数学运算>计算问题之算式计算>速算与技巧>首尾数法
18、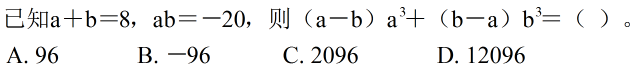 _____
_____
A: AB: BC: CD: D
参考答案: D 本题解释:正确答案是D考点计算问题解析解析1: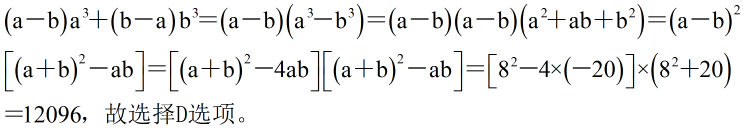
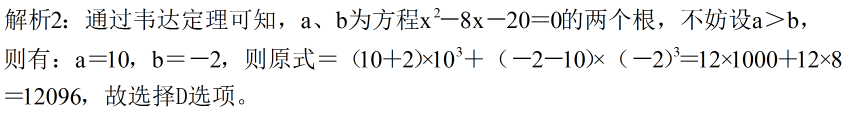 标签完全平方和差公式立方和差公式韦达定理
标签完全平方和差公式立方和差公式韦达定理
19、(101+103+…+199)-(90+92+…+188)=_____。
A: 100 B: 199 C: 550 D: 990
参考答案: C 本题解释:C[解析]提取公因式法。101-90=11,103-92=11,……,199-188=11,总计有50个这样的算式,所以50×11=550,选择C。
20、2010年5月1日世博会开幕,当天是星期六,则2007年3月1日是_____。
A: 星期一B: 星期二C: 星期三D: 星期四
参考答案: D 本题解释:D【解析】由题意2010年5月1日星期六,则与2007年5月1日月份日期相同,根据核心口诀︰①一年就是1——从2007年至2010年是三年,所以加“3”②闰月再加1——从2007年至2010年1个闰月,所以加“1”又由于2007年3月1日至5月1日中间相隔2个月,所以就是“4”,多少再补算——3月31日一个“31”日,加1,故应在2010年5月1日星期六基础上减3+1+4+1=9天,最后可得2007年3月1日是星期四,正确答案为D选项。
21、有若干张卡片,其中一部分写着1.1,另一部分写着1.11,它们的和恰好是43.21。写有1.1和1.11的卡片各有多少张_____
A: 8张,31张B: 28张,11张C: 35张,11张D: 4l张,l张
参考答案: A 本题解释:【答案】A。解析:代入法,8×1.1+31×1.11=43.21,符合题意。
22、某市为鼓励节约用水,对自来水的收费标准作如下规定:每月每户用水不超过10吨的部分,按0.45元/吨收费;超过10吨而不超过20吨的部分,按0.80元/吨收费;超过20吨的部分按1.50元/吨收费,某月甲户比乙户多缴水费7.10元,乙户比丙户多缴水费3.75元。问甲、乙、丙该月各缴水费多少元(按整吨收费)?_____
A: 16元,8.9元,5.15元B: 14元,6.9元,3.15元C: 15元,7.9元,4.15元D: 13元,5.9元,2.15元
参考答案: B 本题解释:参考答案:B题目详解:解法一:如果直接设所缴水费为未知数,等量关系不明显,列方程难度太大,所以可间接设他们的用水量为未知数。设丙户用水为 吨(
吨( 为整数,且
为整数,且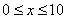 ).乙户用水为
).乙户用水为 吨(
吨( 为整数,且
为整数,且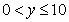 ),因乙户比丙户多缴3.75元,则有
),因乙户比丙户多缴3.75元,则有 ,即
,即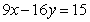 。因为3能整除9和15,但不能整除16,故3必能整除
。因为3能整除9和15,但不能整除16,故3必能整除 ,即
,即 是3的倍数。又经验证,
是3的倍数。又经验证,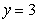 是唯一能使x为整数的值,这时
是唯一能使x为整数的值,这时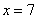 .同理,设甲户用水
.同理,设甲户用水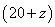 吨(
吨(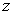 为整数,且
为整数,且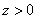 ),因甲户比乙户多缴7.10元,则有:
),因甲户比乙户多缴7.10元,则有: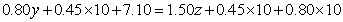 ,即
,即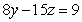 ,把
,把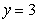 代入,得
代入,得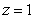 ,故甲户缴纳水费为:
,故甲户缴纳水费为: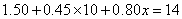 (元),乙户缴纳水费为:
(元),乙户缴纳水费为: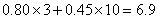 (元),丙户缴纳水费为:
(元),丙户缴纳水费为: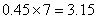 (元)。解法二:观察答案,发现乙的用水量必在10到20吨之间,那么,减去0.45×10=4.5元后,其水费极有可能是0.8的整数倍,只有B符合,验证B中各项,发现正确,故选B考查点:数量关系>数学运算>特殊情境问题>分段计算问题
(元)。解法二:观察答案,发现乙的用水量必在10到20吨之间,那么,减去0.45×10=4.5元后,其水费极有可能是0.8的整数倍,只有B符合,验证B中各项,发现正确,故选B考查点:数量关系>数学运算>特殊情境问题>分段计算问题
23、一条双向铁路上有11个车站,相邻两站都相距7千米。从早晨7点,有18列货车由第11站顺次发出,每隔5分钟发一列,都驶向第一站,速度都是每小时60千米;早晨8点,由第1站发一列客车,向第11站驶出,时速100千米,在到达终点前,货车与客车都不停靠任何一站。那么,在_____,客车能与3列货车先后相遇。
A: 在第四、五站之间B: 在第五、六站之间C: 在第六、七站之间D: 在第七、八站之间
参考答案: B 本题解释:正确答案是B考点行程问题解析铁路上共有11个站,相邻两站相距7千米,则共有70千米的距离,每辆货车之间的距离是5千米。早晨8点,第一列货车已经开出60千米,与第一站相距10千米。客车和第一辆货车相遇时行驶路程为6.25千米,之后每行驶3.125公里即相遇一列货车,则相遇点距第一站点的距离是6.25+3.125n。要使客车在两个站点之间与连续3列货车相遇,则这三列货车中的第一列与客车相遇的地点距离站点不超过:7-3.125×2=0.75千米。即6.25+3.125n除以7余数<0.75,取n=7时商为4,余数为0.125<0.75。则客车行驶在第五、六站之间,分别和第8、9、10辆货车相遇。故正确答案为B。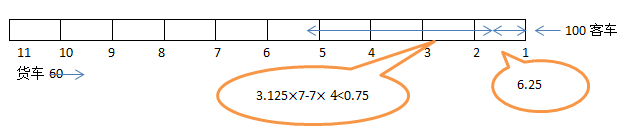 标签画图分析
标签画图分析
24、一个三位数,百位数比十位上的数大4,个位上的数比十位上的数大2,这个三位数恰好是后两个数字组成的两位数的21倍,那么,这个三位数是:_____。
A: 532B: 476C: 676D: 735
参考答案: D 本题解释:正确答案是D考点多位数问题解析百位数比十位上的数大4,只有D选项735符合,故正确答案为D。
25、某市气象局观测发现,今年第一、二季度本市降水量分别比去年同期增加了11%和9%,而两个季度降水量的绝对增量刚好相同。那么今年上半年该市降水量同比增长多少?_____
A: 9.5%B: 10%C: 9.9%D: 10.5%
参考答案: C 本题解释:正确答案是C考点和差倍比问题解析解析1:设绝对增长量是X,则今年上半年的增长量是2X,去年的降水量是X/11%+X/9%,同比增长=2X/(X/11%+X/9%)=9.9%,故正确答案为C。解析2: 标签十字交叉法
标签十字交叉法
26、四个相邻质数之积为17017,他们的和为_____
A: 48B: 52C: 61D: 72
参考答案: A 本题解释: 【解析】A。17017分解因数为17×13×11×7,他们的和为48。参考答案解析
27、我国民间常用十二生肖进行纪年,十二生肖的排列顺序是:鼠、牛、虎、兔、龙、蛇、马、羊、猴、鸡、狗、猪。2011年是兔年,那么2050年是_____。
A: 虎年B: 龙年C: 马年D: 狗年
参考答案: C 本题解释:C。从2011年增加到2050年,需要增加39年,其中前36年为12的倍数,在周期过程中不予考虑。因此2050年为兔向后数3年,即为马年。故选C。
28、甲工人每小时可加工A零件3个或B零件6个,乙工人每小时可加工A零件2个或B零件7个。甲、乙两工人一天8小时共加工零件59个,甲、乙加工A零件分别用时为x小时、y小时,且x、y皆为整数,两名工人一天加工的零件总数相差_____。
A: 6个B: 7个C: 4个D: 5个
参考答案: B 本题解释:正确答案是B考点不定方程问题解析根据题意,甲、乙加工B零件的时间分别为8-x、8-y,则可得:3x+6(8-x)+2y+7(8-y)=59,也即3x+5y=45。由此式可知x能够被5整除,y能够被3整除,而x、y均不超过8,因此x=5,代入解得y=6。甲生产零件总数为3×5+6×3=33个,乙生产零件总数为2×6+7×2=26个,两者相差7个。故答案为B。
29、10个人欲分45个苹果,已知第一个人分了5个,最后一人分了3个,则中间的8人一定存在连续的两人至少分了_____个苹果。
A: 8B: 9C: 10D: 11
参考答案: C 本题解释:【答案】C。解析:中间的8人共分得苹果45—5—3=37(个),将中间的8人分为4组,即(第2、3个人)(第4、5个人)(第6、7个人)(第8、9个人)。由37=9×4+1可知,必有1组,即连续的两人分到了10个苹果。故答案为C。
30、甲、乙两人沿直线从A地步行至B地,丙从B地步行至A地。已知甲、乙、丙三人同时出发,甲和丙相遇后5分钟,乙与丙相遇。如果甲、乙、丙三人的速度分别为85米/分钟、75米/分钟、65米/分钟。问A、B两地距离为多少米?_____
A: 8000米B: 8500米C: 10000米D: 10500米
参考答案: D 本题解释:正确答案是D考点行程问题解析本题理解的重点在于:在甲和丙相遇时,甲比乙多走的距离为后来乙丙一起走的距离。有了这个思想,就容易解出,甲和丙相遇时,甲比乙多走的距离为(75+65)×5=700m,假设甲和丙相遇的时候,甲走了a分钟,则(85-75)a=700,解得a=70。所以两地相距为(85+65)×70=10500米,故正确答案为D。
31、从装满1000克浓度为50%的酒精瓶中倒出200克酒精,再倒入蒸馏水将瓶加满。这样反复三次后,瓶中的酒精浓度是多少?(X)
A: 22.5%B: 24.4%C: 25.6%D: 27.5%
参考答案: 本题解释:正确答案是C考点浓度问题解析解析1:先道出溶液再倒入清水,套用公式,浓度= ,所以答案为C。
,所以答案为C。 解析2:由题意:每次操作后,酒精浓度变为原来的(1000-200)÷1000=0.8,故反复三次后浓度变为50%×0.8×0.8×0.8=25.6%。标签公式应用
解析2:由题意:每次操作后,酒精浓度变为原来的(1000-200)÷1000=0.8,故反复三次后浓度变为50%×0.8×0.8×0.8=25.6%。标签公式应用
32、如下图,梯形ABCD的对角线AC⊥BD,其中AD=1/2,BC=3,AC=2×4/5,BD=2.1。问梯形ABCD的高AE的值是_____。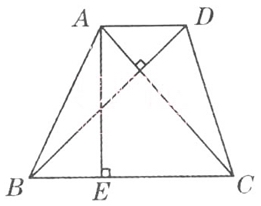
A: 43/24B: 1.72C: 4/252D: 1.81
参考答案: C 本题解释:【解析】由AC×BD=(AD+BC)×AE→AE=42/25。
33、某单位组织党员参加党史、党风廉政建设,科学发展观和业务能力四项培训,要求每名党员参加且只参加其中的两项。无论如何安排,都有至少5名党员参加的培训完全相同,问该单位至少有多少名党员?_____
A: 17B: 21C: 25D: 29
参考答案: C 本题解释:正确答案是C考点抽屉原理问题解析
34、某年级有4个班,不算甲班其余三个班的总人数有131人,不算丁班其余三个班的总人数是134人;乙、丙两班的总人数比甲、丁两班的总人数少1人,问这四个班共有多少人? _____
A: 177B: 176C: 266D: 265
参考答案: A 本题解释:A。【解析】有①乙+丙+丁=131,②甲+乙+丙=134,③乙+丙+1=甲+丁,①-③得丁-1=131-甲-丁,甲=132-2丁,①-②得,甲=丁+3,丁=43,总人数为134+43=177人
35、某区中学生足球联赛共赛8轮(每队均需赛8场)。规则是:胜一场得3分;平一场得1分;负一场得0分。在这次联赛中,A队踢平场数是所负场的2倍,共得17分。问该队胜了几场?_____
A: 2B: 3C: 4D: 5
参考答案: D 本题解释:参考答案 题目详解:设胜了
题目详解:设胜了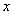 场,负了
场,负了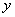 场:
场: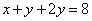 ;
;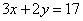 ;
;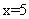 ,
,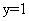 ;胜了5场;所以,选D。考查点:数量关系>数学运算>排列组合问题>比赛问题>循环赛
;胜了5场;所以,选D。考查点:数量关系>数学运算>排列组合问题>比赛问题>循环赛
36、画一个边长为2cm的正方形,再以这个正方形的对角线为边画第二个正方形,再以第二个正方形的对角线为边画第三个正方形,则第三个正方形面积为_____平方厘米。
A: 32B: 16C: 8D: 4
参考答案: C 本题解释:C由题可知第2个正方形对角线长为2cm;则第三个正方形的面积为(2)2=8(平方厘米);正确答案为C。
37、(2005国家,第38题)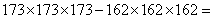 _____。
_____。
A: 926183B: 936185C: 926187D: 926189
参考答案: D 本题解释:参考答案 题目详解:应用首尾数法:解得:
题目详解:应用首尾数法:解得: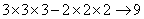 ,所以,选D。考查点:数量关系>数学运算>计算问题之算式计算>速算与技巧>首尾数法
,所以,选D。考查点:数量关系>数学运算>计算问题之算式计算>速算与技巧>首尾数法
38、某次考试100道选择题,每做对一题得1.5分,不做或做错一题扣1分,小李共得100分,那么他答错多少题_____
A: 20B: 25C: 30D: 80
参考答案: A 本题解释:答案:A 解析:不做或做错的题目为(100×1.5-100)÷(1.5+1)=20。
39、某团体从甲地到乙地,甲、乙两地相距100千米,团体中一部分人乘车先行,余下的人步行,先坐车的人到途中某处下车步行,汽车返回接先步行的那部分人,全部人员同时到达。已知步行速度为8千米/小时,汽车速度为40千米/小时。问使团体全部成员同时到达乙地需要多少时间?_____
A: 5.5小时B: 5小时C: 4.5小时D: 4小时
参考答案: B 本题解释:参考答案:B题目详解:根据题意,二队同时出发又同时到达,则二队步行的距离相等,乘车的距离也相等。设第一队乘车的距离是X,则步行的距离是100-X,那么第二队步行的距离也是100-X,汽车从第一队人下车到回来与第二队相遇所行驶的距离(即空车行使的距离)是:100-2×(100-X)=2X-100根据汽车从出发到与第二队相遇所用时间与第二队步行的时间相同,可列方程:[X+(2x-100)]÷40=(100-x)÷8解得,x=75。所用总时间为(以第一队为例):乘车时间+步行时间=(75÷40)+(100-75)÷8=5小时所以,选B。考查点:数量关系>数学运算>行程问题>相遇问题>直线相遇问题>直线一次相遇问题
40、在一次考试中,赵、钱、孙三人的平均分是81分,钱、孙、李三人的平均分是74分,已知赵的分数是93分,那么李的分数是_____
A: 86分B: 75分C: 72分D: 68分
参考答案: C 本题解释:【解析】C。赵、钱、孙三人的总分是81×3=243(分),钱、孙、李三人的总分是74×3=222(分),那么243-222=21(分)就是赵的分数减去李的分数之差,已知赵的分数是93分,则李的分数为93-21=72(分)。
41、现有一种预防禽流感药物配置成的甲、乙两种不同浓度的消毒溶液。若从甲中取2100克,乙中取700克混合而成的消毒浓度为3%;若从甲中取900克,乙中取2700克,则混合而成的溶液的浓度为5%。则甲、乙两种消毒溶液的浓度分别为_____。
A: 3%6%B: 3%4%C: 2%6%D: 4%6%
参考答案: C 本题解释:正确答案是C考点浓度问题解析设两种溶液的浓度分别为a、b,则可列方程2100a+700b=(2100+700)×3%,900a+2700b=(900+2700)×5%,解得a=2%,仅C选项符合,故正确答案为C。秒杀技甲中去2100克,乙中取700克混合而成的消毒溶液浓度为3%,则甲、乙两溶液的浓度必然是一个比3%大,一个比3%小,只有C选项符合,故正确答案为C。
42、甲、乙两人在长30米的泳池内游泳,甲每分钟游37.5米,乙每分钟游52.5米,两人同时分别从泳池的两端出发,触壁后原路返回,如是往返。如果不计转向的时间,则从出发开始计算的1分50秒内两人共相遇了多少次?_____
A: 2B: 3C: 4D: 5
参考答案: B 本题解释:正确答案是B考点行程问题解析解析1:题目的关键在于第一次相遇,两人游过长度之和为泳池长,之后每次相遇,都需要两人再游过两个泳池长。两人一起游一个泳池长,所需时间为30÷(37.5+52.5)×60=20(秒),因此两人分别在20秒时、60秒时、100秒时相遇,共相遇3次。故正确答案为B。解析2:关键点同解析1。直接求出1分50秒两人合起来游过的距离为(37.5+52.5)×110÷60=165(米),为5.5个泳池长。而两人相遇时都恰是合起来游过距离为奇数个泳池长时,也即两人分别在合游1个、3个、5个泳池长时相遇,故共相遇3次。故正确答案为B。解析3:套用公式。先看迎面相遇,30×(2N-1)≤(37.5+52.5)×11/6,得N≤3.25,即有3次迎面相遇;再看追上相遇,30×(2N-1)≤(52.5-37.5)×11/6,得N≤23/24,即没有追及相遇。故总的相遇次数为3次。故正确答案为B。公式:两运动体从两端同时出发,相向而行,不断往返:第N次迎面相遇,两运动体路程和=全程×(2N-1);第N次追上相遇,两运动体路程差=全程×(2N-1)。标签公式应用
43、时针与分针两次垂直的间隔有多长时间?_____
A: 32分B: 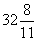 分C: 33分D: 34分
分C: 33分D: 34分
参考答案: B 本题解释:参考答案:B题目详解:解法一:根据公式:时针与分针两次垂直间隔的“静态时间”为30分钟,代入公式算得追及时间为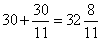 分钟,所以选择B。解法二:根据基本知识点:时针与分针24小时内垂直44次,所以垂直间隔为:
分钟,所以选择B。解法二:根据基本知识点:时针与分针24小时内垂直44次,所以垂直间隔为: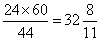 分钟考查点:数量关系>数学运算>特殊情境问题>钟表问题>时针与分针的角度关系
分钟考查点:数量关系>数学运算>特殊情境问题>钟表问题>时针与分针的角度关系
44、有个班的同学去划船,他们算了一下:如果增加一条船,正好可以坐8人,如果减少一条船,正好可以坐12人,问这个班共有多少同学?_____
A: 44B: 45C: 48D: 50
参考答案: C 本题解释:【答案】C。解析:设有船m只,则根据题意可得:8(m+1)=12(m-1),解得m=5。所以这个班共有同学8×(5+1)=48,故正确答案为C。
45、一个长方体的长、宽、高恰好是三个连续的自然数,并且它的体积数值等于它的所有棱长之和的2倍,那么这个长方体的表面积是_____
A: 74B: 148C: 150D: 154
参考答案: B 本题解释: 【解析】B。设该长方体的长、宽、高分别是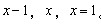 。那么有
。那么有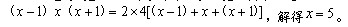 所以这个长方体的表面积为
所以这个长方体的表面积为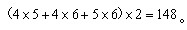
46、四个人夜间过一座独木桥,他们只有一个手电筒,一次同时最多可以有两人一起过桥,而过桥的时候必须有手电筒,所以就得有人把手电筒带来带去,两人同行时以较慢者的速度为准。四人过桥的时间分别是1分、2分、5分、l0分,他们过桥最少需要多少分钟?_____
A: 33B: 31C: 25D: 17
参考答案: D 本题解释:参考答案 题目详解:根据题意,要使得过桥时间最短,则应该保证过桥时间最长的两个人同时过去,但是由于有人把手电筒带来带去,因此,应该保证当这两个人过去后,在河对岸有一个用时比较短的人,把手电筒送回去,设过桥时间分别是l分、2分、5分、10分的人用A、B,C,D表示,可列表如下:
题目详解:根据题意,要使得过桥时间最短,则应该保证过桥时间最长的两个人同时过去,但是由于有人把手电筒带来带去,因此,应该保证当这两个人过去后,在河对岸有一个用时比较短的人,把手电筒送回去,设过桥时间分别是l分、2分、5分、10分的人用A、B,C,D表示,可列表如下: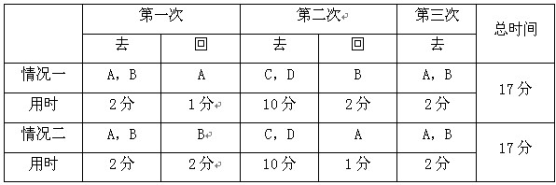 由表可知,答案为D。考查点:数量关系>数学运算>统筹问题>时间统筹问题
由表可知,答案为D。考查点:数量关系>数学运算>统筹问题>时间统筹问题
47、假设五个相异正整数的平均数是15,中位数是18,则此五个正整数中的最大数的最大值可能为_____。
A: 24B: 32C: 35D: 40
参考答案: C 本题解释:参考答案:C题目详解:根据题意:5个数的平均数为15;那么这5个数的和为: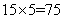 。要使最大数尽量大,那么必须使小的数尽量小;设小的两个数为1和2:又因为中位数是18,那么较大的两个数之和为:
。要使最大数尽量大,那么必须使小的数尽量小;设小的两个数为1和2:又因为中位数是18,那么较大的两个数之和为: ;而这两个数都大于18,所以要使最大的数尽量大:那么使第二大的数为19,所以最大的数为
;而这两个数都大于18,所以要使最大的数尽量大:那么使第二大的数为19,所以最大的数为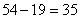 。所以,选C。考查点:数量关系>数学运算>计算问题之算式计算>平均值问题>算术平均值
。所以,选C。考查点:数量关系>数学运算>计算问题之算式计算>平均值问题>算术平均值
48、小刚骑自行车从8路汽车起点出发,沿8路车的行驶路线前进。当他骑了1650米时,一辆8路公共汽车从起点站出发,每分钟行驶450米。这辆汽车在行驶过程中每行5分钟停靠一站,停靠时间为1分钟。已知小刚骑车的速度是汽车行驶速度的,这辆汽车出发后多长时间追上小刚?_____
A: 15分钟B: 16分钟C: 17分钟D: 18分钟
参考答案: C 本题解释:【解析】C。如果不休息的话汽车要1650÷(450-450×)=11分钟,11÷5=2……1,则汽车在追上小刚前休息了2分钟,而这两分钟内,小刚又走了450××2=600米,汽车又要用600÷(450-450×)=4分钟,故一共用了11+4+2=17分钟。
49、某企业有员工500人,其中60%的员工是男性,则该企业男员工比女员工多_____人。
A: 100B: 200C: 300D: 400
参考答案: A 本题解释:正确答案是A考点和差倍比问题解析由题意可得,男性比女性多500×60%-500×40%=100人。故正确答案为A。
50、某大学的文艺社团中,会跳舞的、会吹口琴的会弹古筝的共有38人,其中只会跳舞的有10人,只会吹口琴的有7人,既能弹古筝又会吹口琴的有6人,既会跳舞又会吹口琴的有5人,既会跳舞又会弹古筝的有9人,三种都会的有3人,则只会弹古筝的有多少人?_____
A: 4人B: 6人C: 7人D: 11人
参考答案: C 本题解释:正确答案是C考点容斥原理问题解析解法1:根据已知条件画图分析,有: 于是,只会弹古筝的人数为38-(10﹢6﹢3﹢2﹢7﹢3)=7(人)。故正确答案为C。解法2:由容斥原理,A表示只会一种技能的人数,B表示会两种技能的人数,T表示会三种技能的人数,则由已知条件有:B+3T=6+5+9,T=3,于是B=11;又因A+B+T=38,于是A=38-11-3=24。所以只会弹古筝的人数为24-10-7=7(人),正确答案为C。标签三集合容斥原理公式画图分析
于是,只会弹古筝的人数为38-(10﹢6﹢3﹢2﹢7﹢3)=7(人)。故正确答案为C。解法2:由容斥原理,A表示只会一种技能的人数,B表示会两种技能的人数,T表示会三种技能的人数,则由已知条件有:B+3T=6+5+9,T=3,于是B=11;又因A+B+T=38,于是A=38-11-3=24。所以只会弹古筝的人数为24-10-7=7(人),正确答案为C。标签三集合容斥原理公式画图分析
51、某年级150名同学准备选一名同学在教师节庆祝会上给老师献花。选举的方法是:让150名同学排成一排。由第一名开始报数,报奇数的同学落选退出队列,报偶数的同学站在原位不动,然后再从头报数,如此继续下去,最后剩下的一名当选。小胖非常想去,他在第一次排队时应该站在队列的什么位置才能被选中?_____
A: 64B: 88C: 108D: 128
参考答案: D 本题解释:参考答案 题目详解:第一次报数,“从一开始报数,报奇数的同学退出队列”:故第一次报数,2的倍数原位不动;第二次报数:2的平方的倍数原位不动;第三次报数:2的立方的倍数原位不动;以此类推,到第7次:只剩下2的7次方的倍数原地不动,其余都退出,即排在
题目详解:第一次报数,“从一开始报数,报奇数的同学退出队列”:故第一次报数,2的倍数原位不动;第二次报数:2的平方的倍数原位不动;第三次报数:2的立方的倍数原位不动;以此类推,到第7次:只剩下2的7次方的倍数原地不动,其余都退出,即排在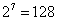 位时才能被选中。所以,选D。考查点:数量关系>数学运算>计算问题之数的性质>奇偶性与质合性问题>奇偶性
位时才能被选中。所以,选D。考查点:数量关系>数学运算>计算问题之数的性质>奇偶性与质合性问题>奇偶性
52、四人进行篮球传接球练习,要求每人接球后再传给别人。开始由甲发球,并作为第一次传球,若第五次传球后,球又回到甲手中,则共有传球方式_____。
A: 60种B: 65种C: 70种D: 75种
参考答案: A 本题解释:[解析]正确答案为A。细分一下传球路径,第一次接球的人只能是非甲,第二第三次接球的人可能是甲或非甲,第四次接球的人只能是非甲,第五次接球的人一定是甲,每次传球后接到球的人可分析如下:第一次第二次第三次第四次第五次第一种情况:非甲甲非甲非甲甲第二种情况:非甲非甲甲非甲甲第三种情况:非甲非甲非甲非甲甲按排列组合,第一种情况的传球方式有3×1×3×2×1=18,第二种有3×2×1×3×1=18,第三种情况有3×2×2×2×l=24,相加共有60种,故选A。
53、一容器内有浓度为30%的糖水,若再加入30千克水与6千克糖,则糖水的浓度变为25%。问原来糖水中含糖多少千克?_____
A: 5:6B: 1:1C: 6:5D: 4:3
参考答案: B 本题解释:正确答案是B考点行程问题解析解析1:根据题意,甲乙两人用时分别为1.5小时、1小时,时间比为3:2,速度比为2:3,因此路程比为1:1,故正确答案为B。解析2:甲的速度是乙的2/3,设甲、乙的速度分别为2、3,则甲走过的路程为2×(1+0.5)=3,乙为3×1=3,因此路程比为1:1。故正确答案为B。标签赋值思想比例转化
54、某商场以摸奖的方式回馈顾客,盒内有五个乒乓球,其中一个为红色,2个为黄色,2个为白色,每位顾客从中任意摸出一个球,摸到红球奖10元,黄球奖1元,白球无奖励,则每一位顾客所获奖励的期望值为多少?_____
A: 10B: 1.2C: 2D: 2.4
参考答案: D 本题解释:正确答案是D考点概率问题解析根据已知,每一位顾客所获奖励的期望值为10×1/5+1×2/5=2.4,故正确答案为D。
55、10个连续偶数的和是以1开始的10个连续奇数和的2.5倍,其中最大的偶数是多少?_____
A: 34B: 38C: 40D: 42
参考答案: A 本题解释:参考答案:A题目详解:[解析]根据题意,可知:以1开始的10个连续奇数和为: =100;那么,10个连续偶数的和为100×2.5=250,设最大的偶数是x,根据等差数列求和公式,则:
=100;那么,10个连续偶数的和为100×2.5=250,设最大的偶数是x,根据等差数列求和公式,则: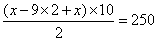 ,解得x=34。所以,选A。考查点:数量关系>数学运算>计算问题之算式计算>数列问题>数列求和>单一数列求和>等差数列求和
,解得x=34。所以,选A。考查点:数量关系>数学运算>计算问题之算式计算>数列问题>数列求和>单一数列求和>等差数列求和
56、银行存款年利率为2.5%,应纳利息税20%,原存1万元1年期,实际利息不再是250元,为保持这一利息收入,应将同期存款增加到_____元。
A: 15000B: 20000C: 12500D: 30000
参考答案: C 本题解释:C。【解析】令存款为x,为保持利息不变,250=x×2.5%×(1-20%)=>x=12500。
57、某天体沿正圆形轨道绕地球一圈所需时间为29.53059天,转速约1公里/秒。假设该天体离地球的距离比现在远10万公里而转速不变,那么该天体绕地球一圈约需要多少天?_____
A: 31 B: 32 C: 34 D: 37
参考答案: D 本题解释: D。算式为[29.53059×24×60×60×1/π+100000×2]×π÷1÷60÷60÷24≈36.8天,所以答案为D项。
58、 _____
_____
A: AB: BC: CD: D
参考答案: C 本题解释:正确答案是C考点计数模型问题解析 故正确答案为C。标签公式应用
故正确答案为C。标签公式应用
59、已知4/15=(1/A)+(1/B),A、B为自然数,且A≥B,那么A有几个不同的值?_____
A: 2B: 3C: 4D: 5
参考答案: B 本题解释:正确答案是B考点不等式分析问题解析 标签直接代入
标签直接代入
60、一张考试卷共有10道题,后面的每一道题的分值都比前面一道题多2分。如果这张考卷的满分为100分,那么第8道题的分值应为多少?_____
A: 14B: 15C: 16D: 17
参考答案: B 本题解释:正确答案是B考点数列问题解析10道题的分值是公差为2的等差数列。设第一道题的分值为y,则第10道题的分值为y+2×(10-1)=y+18。由题意得(y+y+18)×10÷2=100,解得y=1,则第8道题的分值为1+2×(8-1)=15分,故正确答案为B。
61、甲乙两个乡村阅览室,甲阅览室科技类书籍数量的1/5相当于乙阅览室该类书籍的1/4,甲阅览室文化类书籍数量的2/3相当于乙阅览室该类书籍的1/6,甲阅览室科技类和文化类书籍的总量比乙阅览室两类书籍的总量多1000本,甲阅览室科技类书籍和文化类书籍的比例为20:1,问甲阅览室有多少本科技类书籍?_____
A: 15000B: 16000C: 18000D: 20000
参考答案: D 本题解释:答案:D.[解析]假设甲阅览室科技类书籍有20x本,文化类书籍有x本,则乙阅读室科技类书籍有16x本,文化类书籍有4x本,由题意有:(20x+x)-(16x+4x)=1000,解出x=1000,则甲阅览室有科技类书籍20000本。
62、甲、乙、丙、丁四人为灾区捐款,甲捐款数是另外三人捐款总数的一半,乙捐款数是另外三人捐款总数的1/3,丙捐款数是另外三人捐款总数的1/4,丁捐款169元。问四人一共捐了多少钱?_____
A: 780元B: 890元C: 1183元D: 2083元
参考答案: A 本题解释:正确答案是A考点和差倍比问题解析设捐款总数为60x元,则由“甲捐款数是另外三人捐款总数的一半”得到甲捐款20x元;由“乙捐款数是另外三人捐款总数的1/3”得到乙捐款15x元;由“丙捐款数是另外三人捐款总数的1/4”得到甲捐款12x元。由题意得方程:20x+15x+12x+169=60x解得x=13因此60x=780,故正确答案为A。秒杀技由“甲捐款数是另外三人捐款总数的一半”可知捐款总数必须能被3整除,故只有A选项符合,故正确答案为A。
63、有甲、乙两只盒子,甲盒装有2个黑球、4个红球,乙盒装有4个黑球、3个红球,若从甲、乙两盒中各任取两球交换后,甲盒中恰有4个红球的概率为多少?_____
A:  B:
B: 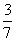 C:
C: 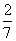 D:
D: 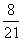
参考答案: D 本题解释:参考答案 题目详解:事件“甲盒中恰有4个红球”发生:说明从甲盒任取两球的结果与从乙盒任取两球的结果相同;甲盒任取两个球:有
题目详解:事件“甲盒中恰有4个红球”发生:说明从甲盒任取两球的结果与从乙盒任取两球的结果相同;甲盒任取两个球:有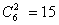 种情形,其中“2黑”的情形有
种情形,其中“2黑”的情形有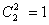 种,“1黑1红”的情形有
种,“1黑1红”的情形有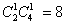 种,“2红”的情形有
种,“2红”的情形有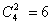 种;乙盒任取两个球:有
种;乙盒任取两个球:有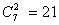 种情形,其中“2黑”的情形有
种情形,其中“2黑”的情形有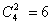 种,“1黑1红”的情形有
种,“1黑1红”的情形有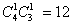 种,“2红”的情形有
种,“2红”的情形有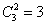 种。所以,“2黑”交换:
种。所以,“2黑”交换: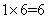 种;“1黑1红”交换:
种;“1黑1红”交换: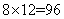 种;“2红”交换:
种;“2红”交换: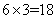 种;因此,甲盒中恰有4个红球的概率是:
种;因此,甲盒中恰有4个红球的概率是: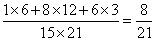 ;所以,选D。考查点:数量关系>数学运算>概率问题>条件概率
;所以,选D。考查点:数量关系>数学运算>概率问题>条件概率
64、某三年制普通初中连续六年的在校生人数分别为:X1,X2,X3,X4,X5,X6.假设该校所有学生都能顺利毕业,那么前三年的入学学生总数与后三年的入学学生总数之差为_____
A: (X1+X2+X3)-(X4+X5+X6) B: X1-X4C: X3-X6 D: (X3-X1)-(X6-X4)
参考答案: C 本题解释:【解析】C.考查整体思维。前三年入学学生人数本质上就是第三年的在校生人数X3(第三年在校生的初三、初二、初一分别为前三年的入学人数),类似的,X6即为后三年的入学人数。故答案为X3-X6.
65、某服装店三月份男装和女装的总销售额为8000元,已知三月份女装销售了50件,每件售价100元,则三月份男装销售额为_____元。
A: 1000B: 2000C: 3000D: 4000
参考答案: C 本题解释:正确答案是C考点和差倍比问题解析由题意可得,三月份男装销售额为8000-50×100=3000元。故正确答案为C。
66、某产品售价为67.1,在采用新技术生产节约10%成本之后,售价不变,利润可可比原来翻一番。则该产品最初的成本为_____元。
A: 51.2B: 54.9C: 61D: 62.5
参考答案: C 本题解释:正确答案是C考点经济利润问题解析由题意可知,节约的10%成本与原利润相等,设成本为n,则有67.1-n=0.1n,解得n=61。故正确答案为C。
67、(2008安徽,第12题)某日小李发现日历有好几天没有翻,就一次翻了6张,这6天的日期加起来数字是141,他翻的第一页是几号?_____
A: 18B: 2lC: 23D: 24
参考答案: B 本题解释:参考答案:B题目详解:六个日期之和为141:平均数(即“中位数”)应该是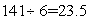 ;因此这六个数的中位数为23.5;故这六个日期分别为:21、22、23、24、25、26;则翻的第一天是2l号;所以,选B。考查点:数量关系>数学运算>特殊情境问题>日期星期问题
;因此这六个数的中位数为23.5;故这六个日期分别为:21、22、23、24、25、26;则翻的第一天是2l号;所以,选B。考查点:数量关系>数学运算>特殊情境问题>日期星期问题
68、先将线段AB分成20等份,线段上的等分点用”△”标注,再将该线段分成21等份,等分点用”O”标注(A、B两点都不标注),现在发现”△”和”O”之间的最短处长为2厘米,问线段AB的长度为多少?_____
A: 2460厘米B: 1050厘米C: 840厘米D: 680厘米
参考答案: C 本题解释:正确答案是C考点和差倍比问题解析 秒杀技线段能分成20份,也可分成21份,则线段长肯定能被420(20与21的最小公倍数)整除,只有C符合条件。标签最小公倍数数字特性
秒杀技线段能分成20份,也可分成21份,则线段长肯定能被420(20与21的最小公倍数)整除,只有C符合条件。标签最小公倍数数字特性
69、社区活动中心有40名会员,全部由老人和儿童组成。第一次社区活动组织全体老年会员参加,第二次活动组织全体女性成员参加。结果共有12人两次活动全部参加,6人两次活动全未参加。已知老人与儿童的男女比例相同,且老人数量多于儿童,问社区活动中心的会员中,老人,儿童各多少名?_____
A: 3010B: 1822C: 2812D: 2515
参考答案: A 本题解释:正确答案是A考点和差倍比问题解析解析1:由题意可知12人为女性老会员,有6人为男性儿童。假定男性老会员为x名,则女性儿童有(40-12-6-x)人,根据题意可得:x:12=6:(40-12-6-x),解得x=18或x=4(不合题意,舍去)。因此老人、儿童分别有30、10人,故正确答案为A。
70、已知ab+6=c,其中a和b都是小于1000的质数,c是偶数,那么c的最大的数值是多少?_____
A: 1500B: 1600C: 2000D: 2100
参考答案: C 本题解释:参考答案:C题目详解:因为和c是偶数,加数中6是偶数:所以ab的积也是一个偶数;因为两个都是质数:所以当中必有一个是2;要想使得和c最大:那么另一个质数就必须是小于1000的最大的质数997;所以c=2×997+6=2000;所以,选C。考查点:数量关系>数学运算>计算问题之数的性质>奇偶性与质合性问题>质合性
71、173×173×173-162×162×162=_____。
A: 926183B: 936185C: 926187D: 926189
参考答案: D 本题解释:答案:D【解析】利用简单的猜测法。173的尾数是3,3的立方为27;162的尾数是2,2立方为8。两者相减尾数为9,所以判断173和162的立方之差的尾数为9。所以答案为D项。
72、股票买入和卖出都需要通过证券公司进行交易,每次交易手续费占交易额的 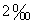 ,某人以10元的价格买入1000股股票,几天后又以12元的价格全部卖出,若每次交易还需付占交易额
,某人以10元的价格买入1000股股票,几天后又以12元的价格全部卖出,若每次交易还需付占交易额  的印花税,则此人将获利_____。
的印花税,则此人将获利_____。
A: 1880元B: 1890元C: 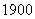 元D: 1944元
元D: 1944元
参考答案: B 本题解释:参考答案:B题目详解:每次交易损失为:2‰+3‰=5‰故将获利:1000×12-1000×10-1000×10×5‰-1000×12×5‰=1890所以,选B。考查点:数量关系>数学运算>利润利率问题>成本、售价、利润、利润率之间的等量关系问题
73、某企业在转型中,对部分人员进行分流,并提供了以下四种分流方案,供被分流人员人选一种。方案一:一次性领取补贴2万元,同时按现有年薪的200%一次性领取医疗费;方案二:每年按现有年薪的25%领取补贴,直到60岁退休,无医疗费;方案三:每年按现有年薪的30%领取补贴,并领取1000元的医疗费,连续领取十年;方案四:一次性领取补贴4万元,无医疗费;该企业某职工今年45岁,按规定被分流,他的现有年薪为9600元,按照分流方案规定,对他最有利的是_____。
A: 方案一B: 方案二C: 方案三D: 方案四
参考答案: D 本题解释:正确答案是D考点和差倍比问题解析方案一:该职工可以获得20000+9600×2=39200元;方案二:该职工可以获得9600×25%×15=36000元;方案三:该职工可以获得(9600×30%+1000)×10=38800元;方案四:该职工可以获得4万元。因此对他最有利的是方案四,故正确答案为D。
74、银行整存整取的年利率是:2年期为2.25%,3年期为2.52%,5年期为2.79%,如果甲、乙二人同时各存入1万元,甲先存2年期,到期后连本带利改存为3年期;乙存5年期。5年后,2人同时取出,那么两人的收益差为多少元?_____
A: 64B: 102C: 155D: 234
参考答案: C 本题解释:C【解析】 甲5年后取出本利和为:10000×(1+2.25%×2)×(1+2.52%×3)=10000×1.045×1.0756=11240(元)乙5年后取出本利和为:10000×(1+2.79%×5)=1000×1.1395=11395由此可见,乙的收益多。11395-11240=155(元)。故选C。
75、小王的手机通讯录上有一手机号码,只记下前面8个数字为15903428。但他肯定,后面3个数字全是偶数,最后一个数字是6,且后3个数字中相邻数字不相同,请问该手机号码有多少种可能?_____
A: 15B: 16C: 20D: 18
参考答案: B 本题解释:后三位全是偶数,且三数中相邻数字不同,已知最后一位是6,所以倒数第二位有0、2、4、8四种可能,倒数第三位来源:91考试网 91EXAm.org也有四种可能性,故该手机号码有4×4=16(种)可能。
76、长方形ABCD的面积是72平方厘米,E、F分别是CD、BC的中点,三角形AEF的面积是多少平方厘米?_____ 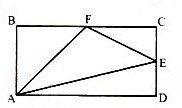
A: 24B: 27C: 36D: 40
参考答案: B 本题解释:正确答案是B考点几何问题解析三角形AEF虽然为规则几何图形,但不是特殊的三角形,且三边值未知,若正面求解较为麻烦。从逆向考虑,注意到△AEF可以看作长方形依次去除周围三个三角形得到。由比例关系可知,△ABF为长方形的1/4,△ADE为长方形的1/4,而△ECF为长方形的1/8,因此△AEF为长方形大小的3/8,故可知其面积为27,故正确答案为B。标签逆向考虑
77、(2008陕西,第13题)一根竹笋从发芽到长大,如果每天长一倍,经过10天长到40分米,那么长到2.5分米时,要经过多少天?_____
A: 6B: 8C: 4D: 12
参考答案: A 本题解释:参考答案:A题目详解:设竹笋原长A,N天长到2.5分米,则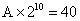 ,
,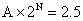 ,得N=6。考查点:数量关系>数学运算>计算问题之算式计算>数列问题>求第N项>等比数列第N项
,得N=6。考查点:数量关系>数学运算>计算问题之算式计算>数列问题>求第N项>等比数列第N项
78、篮球队教练要召集队员研究问题,要尽快通知到全部29名队员,通过电话通知最快,每个电话用一分钟。那么需要几分钟?_____
A: 3B: 4C: 5D: 7
参考答案: C 本题解释:参考答案:C题目详解:第1分钟:教练通知一个队员;第2分钟:教练的先前得到消息的队员共2人可以通知另外2个队员,这时总共有3个队员得到消息;第3分钟:教练的先前得到消息的队员共4人可以通知另外4个队员,这时总共有7个队员得到消息;第4分钟:教练的先前得到消息的队员共8人可以通知另外8个队员,这时总共有15个队员得到消息;第5分钟:教练的先前得到消息的队员共16人可以通知另外16个队员,这时总共有31个队员得到消息。所以,29名队员最多5分钟可以通知到。考查点:数量关系>数学运算>统筹问题>时间统筹问题
79、一个正方体木块放在桌子上,每一面都有一个数,位于对面两个数的和都等于13,小张能看到顶面和两个侧面,看到的三个数和为18;小李能看到顶面和另外两个侧面,看到的三个数的和为24,那么贴着桌子的这一面的数是多少?_____
A: 4B: 5C: 6D: 7
参考答案: B 本题解释:正确答案是B考点趣味数学问题解析题目给出对面数字之和为13,则注意将其余条件中出现的对面合在一起。从这一点出发,可以看出若将小张与小王看到的面合在一起,则实际共看到2个顶面与4个不同的侧面。而四个不同侧面恰为两组对面,也即其数字之和为:13×2=26,因此顶面的数字为:(18+24-26)÷2=8,于是底面数字为:13-8=5,故正确答案为B。
80、高速公路上行驶的汽车A的速度是每小时100公里,汽车B的速度是每小时120公里,此刻汽车A在汽车B前方80公里处,汽车A中途加油停车10分钟后继续向前行驶。那么从两车相距80公里处开始,汽车B至少要多长时间可以追上汽车A?_____
A: 2小时B: 3小时10分C: 3小时50分D: 4小时10分
参考答案: B 本题解释:正确答案是B考点行程问题解析汽车A在加油的10分钟时间内汽车B可行驶路程120×1/6=20公里,A、B间剩余80-20=60公里是A、B追及的过程,用时60÷(120-100)=3小时,因此汽车B追上A共用时3小时10分钟,故正确答案为B。
81、大小猴子共35只,它们一起去采摘水蜜桃。猴王不在的时候,一只大猴子一小时可采15千克,一只小猴子一小时可采摘11千克。猴王在场监督的时候,每只猴子不论大小每小时都可多采摘12千克。有一天,采摘了8小时,其中只有第一小时和最后一小时有猴王在场监督,结果共采摘了4400千克水蜜桃。在这个猴群中,共有小猴子多少只?_____
A: 18B: 20C: 22D: 24
参考答案: B 本题解释:正确答案是B考点鸡兔同笼问题解析解析1:设猴群中小猴有n只,则[(15+12)×(35-n)+(11+12)n]×2+[15×(35-n)+11n]×6=4400,可得n=20。解析2:我们可以先把35只猴子全部看成小猴子,那么这8小时可完成量为11×35×8+12×35×2=3920。然后分析差异,大猴子每小时比小猴子多采15-11=4,可得大猴子的数量为(4400-3920)÷8÷4=15,故小猴子数量为20。所以正确答案为B。标签差异分析
82、有一批书,分给公司的所有人,若每人一本,则还差19本,若每个部门派7本,则多出1本。如果再招聘2个人进公司。则正好每个部门有9人,问:总共有_____个部门。
A: 11B: 9C: 7D: 5
参考答案: A 本题解释:A。
83、在一周长为50m的圆形花坛周围种树,如果每隔5m种一颗,共要种_____棵树。
A: 9B: 10C: 11D: 12
参考答案: B 本题解释:正确答案是B考点计数模型问题解析根据圆周植树计算模型,始端与终端重合,故一共需种50÷5=10棵树,正确答案为B。标签公式应用
84、一次知识竞赛,共3道题,每个题满分6分。给分时只能给出自然数0—6分。如果参加竞赛的人三道题的得分的乘积都是36分,并且任意两人三道题的得分不完全相同,那么最多有多少人参加竞赛? _____
A: 24B: 20C: 18D: 12
参考答案: D 本题解释:【解析】D。解析:36=1×6×6=2×3×6=3×3×4,三道题得1,6,6分有3种可能,三道题得2,3,6分有6中可能,三道题得3,3,4分有3种可能。故最多有3+6+3=12人。
85、某工厂有一大型储水罐供全厂生产用水,已知每天晚8点至早8点蓄水,蓄水管流量为8吨/小时,工厂用水为每天早8点至晚12点,用量为6吨/时,储水罐中水位最高时的储水量至少是_____。
A: 48吨B: 72吨C: 84吨D: 96吨
参考答案: B 本题解释:B【解析】从每晚8点开始蓄水,至早8点水位一直在升高,在这之后,蓄水停止,水位下降;晚8点至晚12点之间,水位上升,但同时仍在用水。故水位最高点应为早8点。8×(12一4)+4×(8一6)=72(吨)。
86、有120名职工投票从甲、乙、丙三人中选举一人为劳模,每人只能投一次,且只能选一个人,得票最多的人当选。统计票数的过程发现,在前81张票中,甲得21票,乙得25票,丙得35票。在余下的选票中,丙至少再得几张选票就一定能当选?_____
A: 15B: 18C: 21D: 31
参考答案: A 本题解释:正确答案是A考点抽屉原理问题解析解析1:整体考虑,乙和丙的票数较接近,乙对丙的威胁最大。考虑最坏情况,剩余的39张票均投给乙、丙。乙丙共可以分120-21=99张选票,均得49张时,仍不能保证丙一定当选,再得剩余的一张选票,即丙得50张选票时,保证当选。所以还需要50-35=15张。故正确答案为A。解析2:乙和丙的票数较接近,乙对丙的威胁最大,考虑最坏的情况,在剩余的39张票中,只在乙丙中分配。先分给乙10张,此时乙丙都得35票,还剩29票,如果乙和丙均再得14张选票,二者票数相同,丙仍然不能保证当选,于是丙需要再得1张选票,即在最后29票中只要分15票给丙,就可以保证丙必然当选。故正确答案为A。
87、有一排长椅总共有65个座位,其中已经有些座位上有人就坐。现在又有一人准备找一个位置就坐,但是此人发现,无论怎么选择座位,都会与已经就坐的人相邻。问原来至少已经有多少人就坐?_____
A: 13B: 17C: 22D: 33
参考答案: C 本题解释:正确答案是C考点抽屉原理问题解析分析一下,无论怎么选择座位,都会与已经就坐的人相邻,意味着,长椅两端最靠边的位置上最多只空了1个座位,而中间人与人之间最多只空了2个座位。从至少已经有多少人就坐有角度来看,假设第2个座位上有人的话,第5、8、11……62、65个座位分别有人,这样的结果需要人最少。从总人数来说,也就是说每3个位置坐1人,所以很显然是22人,故正确答案为C。
88、大学四年级某班共有50名同学,其中奥运会志愿者10人,全运会志愿者17人,30人两种志愿者都不是,则班内是全运会志愿者而非奥运会志愿者的同学为多少?_____
A: 3B: 7C: 10D: 17
参考答案: C 本题解释:正确答案是C考点容斥原理问题解析根据题意,班内既是全运会志愿者又是奥运会志愿者的同学有(10+17)-(50-30)=7人,所以是全运会志愿者而非奥运会志愿者的同学有17-7=10人。故正确答案为C。
89、某高校2006年度毕业学生7650名,比上年度增长2%,其中本科生毕业数量比上年度减少2%,而研究生毕业数量比上年度增加10%,那么,这所高校今年毕业的本科生有_____。
A: 3920人B: 4410人C: 4900人D: 5490人
参考答案: C 本题解释:正确答案是C考点和差倍比问题解析假设去年研究生毕业数为A,本科生毕业数为B,那么今年研究生毕业数为1.1A,本科生毕业数为0.98B。由题意知:A+B=7650÷(1+2%),1.1A+0.98B=7650,解得B=5000人。则今年本科生毕业数量为5000×0.98=4900人,故正确答案为C。秒杀技由“本科生比上年度减少2%”可知“今年本科生数=98%×去年本科生数”(注意98%是百分数,本质上也是个分数),所以今年本科生应能够被49整除。由“研究生毕业数量比上年增加10%”知“今年研究生数=110%×去年研究生数”,所以今年研究生数应能够被11整除,据此两条得出正确答案为C。
90、某单位选举工会主席,每人投票从甲、乙、丙三个候选人中选择一人。已知该单位共有52人,并且在计票过程中的某时刻,甲得到17票,乙得到16票,丙得到11票。如果得票比其它两人都多的候选人将成为工会主席,那么甲最少再得到多少票就能够保证当选?_____
A: 2B: 3C: 4D: 5
参考答案: C 本题解释:正确答案是C考点抽屉原理问题解析剩余的票数为:52-17-16-11=8,假设甲得4票,乙得4票,那甲仅以一票的优势当选,此时再少一票甲就不能保证当选,因此甲最少再得4张票就能保证当选,故正确答案为C。标签构造调整
91、三个连续的偶数的乘积为192,那么其中最大的数是多少?_____
A: 4B: 6C: 12D: 8
参考答案: D 本题解释:答案:D【解析】设最小的偶数为x,则这三个偶数依次为x,x+2,x+4,故x?(x+2)?(x+4)=192。用代入法解答。经过验证x=4,则最大的偶数为8。因此正确答案为D。
92、3×999+8×99+4×9+15的值是_____。
A: 3866B: 3855C: 3840D: 3877
参考答案: C 本题解释:正确答案是C考点计算问题解析计算原式个位上的数字,7+2+6+5=20,个位数为0,故正确答案为C。
93、一件商品相继两次分别按折扣率为10%和20%进行折扣,已知折扣后的售价为540元,那么折扣前的售价为_____。
A: 600元B: 680元C: 720元D: 750元
参考答案: D 本题解释:正确答案是D考点和差倍比问题解析由题意可知折扣前售价为:540÷(1-20%)÷(1-10%)=750元,故正确答案为D。
94、甲、乙两个冷藏库共存鸡蛋6250箱,先从甲库运走1100箱后,这时乙库存的鸡蛋比甲库剩下的2倍还多350箱,求甲库比乙库原来少存了鸡蛋多少箱?_____
A: 550B: 650C: 750D: 850
参考答案: D 本题解释:参考答案 题目详解:根据题意,可知:甲库运走l100箱以后,则:两库还剩下:6250-1100=5150箱,甲库还剩下:(5150-350)÷(1+2)=1600箱;那么,则有:甲库原存鸡蛋为:1600+1100=2700箱,乙库原来存鸡蛋为:1600×2+350=3550箱,甲库比乙库少:3550-2700=850箱。考查点:数量关系>数学运算>和差倍比问题>和差倍问题
题目详解:根据题意,可知:甲库运走l100箱以后,则:两库还剩下:6250-1100=5150箱,甲库还剩下:(5150-350)÷(1+2)=1600箱;那么,则有:甲库原存鸡蛋为:1600+1100=2700箱,乙库原来存鸡蛋为:1600×2+350=3550箱,甲库比乙库少:3550-2700=850箱。考查点:数量关系>数学运算>和差倍比问题>和差倍问题
95、某企业有甲、乙、丙三个仓库,且都在一条直线上,之间分别相距1千米、3千米,三个仓库里面分别存放货物5吨、4吨、2吨。如果把所有的货物集中到一个仓库,每吨货物每千米运费是90元,请问把货物放在哪个仓库最省钱?_____
A: 甲 B: 乙 C: 丙 D: 甲或乙
参考答案: B 本题解释:【解析】B。假设都运到甲仓库,供需运费为90×(4×3+2×4)=1800元,若均运到乙仓库,则需运费90×(5×1+2×3)=990元,若运到丙仓库,则需运费90×(5×4+4×3)=2820元,所以应该将货物运到乙仓库。
96、已知甲的13%为14,乙的14%为15,丙的15%为16,丁的16%为17,则甲、乙、丙、丁四个数中最大的数是_____。
A: 甲B: 乙C: 丙D: 丁
参考答案: A 本题解释:正确答案是A考点和差倍比问题解析
97、一项工程由甲单独做需要15天做完,乙单独做需要12天做完,二人合做4天后,剩下的工程由甲单独做,还需做几天方可做完?_____。
A: 6 B: 8C: 9 D: 5
参考答案: A 本题解释:A 【解析】依题意,甲每天完成总工程的1/15,乙每天完成总工程的1/12,甲、乙合作4天共完成(1/12+1/15) ×4=3/5,故剩下的工程甲需要的时间为(1—3/5)/(1/15)=6,总计算式即为[1一(1/12+1/15)]×4/(1/15)=6(天)。
98、有面值为8分、1角和2角的三种纪念邮票若干张,总价值为1元2角2分,则邮票至少有_____。
A: 7张B: 8张C: 9张D: 10张
参考答案: C 本题解释:C【解析】要使邮票最少,则要尽量多的使用大面额邮票,所以要达到总价值,2角的邮票要使用4张,1角的邮票要使用1张,8分的邮票要4张,这样使总价值正好为1元2角2分,所以要用9张。
99、某班学生不到50人,在一次考试中,有1/7人得优,1/3人得良,1/2人及格,其余的均不及格,那么不及格的人数是_____
A: 1 B: 2 C: 3 D: 4
参考答案: A 本题解释: A。通过题干可知,该班级最少人数应为7、3、2的最小公倍数,又因为不能超过50人,所以该班人数为7×3×2=42人。那么不及格的人数为42…61421=1。故正确答案为A。
100、小明用5天时间看完了一本200页的故事书。已知第二天看的页数比第一天多,第三天看的页数是第一、二两天看的页数之和,第四天看的页数是第二、三两天看的页数之和,第五天看的页数是第三、四两天看的页数之和。那么小明第五天至少看了_____页。
A: 84B: 78C: 88D: 94
参考答案: A 本题解释:【答案】A。解析:设小明第一天看了a页,第二天看了b页,则前五天看的页数依次为a,b,a+b,a+2b,2a+3b。这些数的和是200,可得5a+7b=200。因为5a与200都是5的倍数,所以b是5的倍数。因为ba,所以上式只有两组解b=20,a=12;b=25,a=5。将这两组解分别代入2a+3b,得到第五天至少看了84页。