微信搜索关注"91考试网"公众号,领30元,获取公务员、事业编、教师等考试资料40G!
1、李大夫去山里给一位病人出诊,他下午1点离开诊所,先走了一段平路,然后爬上了半山腰,给那里的病人看病。半小时后,他沿原路下山回到诊所,下午3点半回到诊所。已知他在平路步行的速度是每小时4千米,上山每小时3千米,下山每小时6千米。请问:李大夫出诊共走了多少路?_____
A: 5千米B: 8千米C: 10千米D: l6千米
参考答案: B 本题解释: 
2、某旅游部门规划一条从甲景点到乙景点的旅游线路,经测试,旅游船从甲到乙顺水匀速行驶需3小时;从乙返回甲逆水匀速行驶需4小时,假设水流速度恒定,甲乙之间的距离为y公里,旅游船在静水中匀速行驶y公里需x小时,则x满足的方程为_____。
A: AB: BC: CD: D
参考答案: D 本题解释:正确答案是D考点行程问题解析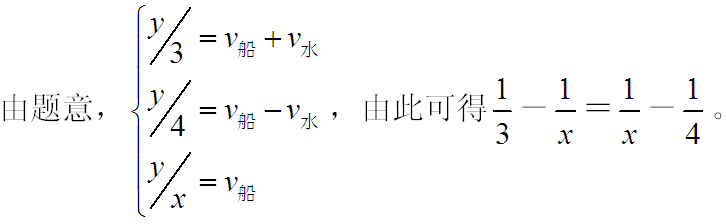 因此正确答案为D。秒杀技在顺流或逆流的行程过程中,建立关系式时不会对时间相加减,而只能对速度相加减,因此选项A、B不符合;船在静水中的速度必然介于逆流速度和顺流速度之间,因此选项C不符合,而选项D符合。故正确答案为D。
因此正确答案为D。秒杀技在顺流或逆流的行程过程中,建立关系式时不会对时间相加减,而只能对速度相加减,因此选项A、B不符合;船在静水中的速度必然介于逆流速度和顺流速度之间,因此选项C不符合,而选项D符合。故正确答案为D。
3、某地区水电站规定,如果每月用电不超过24度,则每度收9分钱,如果超过24度,则多出度数按每度2角收费,若某月甲比乙多交了9.6角,则甲交了_____。
A: 27角6分B: 26角4分C: 25角5分D: 26角6分
参考答案: A 本题解释:参考答案:A题目详解:解法一:根据题意,由于甲比乙多交的96分,既不是20的倍数也不是9的倍数,因此,甲比乙多交的电费应由每度9分和每度2角两部分构成,即 ,故甲超过标准用电量3度,需要交
,故甲超过标准用电量3度,需要交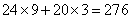 分。因此,选A,解法二:根据某月甲比乙多交了9.6角可知,该月甲用电量必超过24度,而乙没有超过标准用电量,假设甲用电量为
分。因此,选A,解法二:根据某月甲比乙多交了9.6角可知,该月甲用电量必超过24度,而乙没有超过标准用电量,假设甲用电量为 ,乙用电量为y,则
,乙用电量为y,则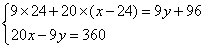 因为360,9能被3整除,
因为360,9能被3整除,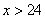 ,有
,有 =27,30……当
=27,30……当 =27时,
=27时,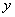 =20,正确,因此,甲需要交
=20,正确,因此,甲需要交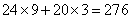 分。因此,选A考查点:数量关系>数学运算>特殊情境问题>分段计算问题
分。因此,选A考查点:数量关系>数学运算>特殊情境问题>分段计算问题
4、建华中学共有1600名学生,其中喜欢乒乓球的有1180人,喜欢羽毛球的有1360人,喜欢篮球的有1250人,喜欢足球的有1040人,问以上四项球类运动都喜欢的至少有几人?_____
A: 20人B: 30人C: 40人D: 50人
参考答案: B 本题解释:【答案】B。解析:采取逆向思维法。不喜欢乒乓的1600-1180=420,不喜欢羽毛球的1600-1360=240,不喜欢篮球的1600-1250=350,不喜欢足球的1600-1040=560,要使四项运动都喜欢的人数最少,那么不喜欢的人数就要最多那么都尽量不相交,从而达到最多:420+240+350+560=1570人,所以喜欢的最少的为1600-1570=30人,故正确答案为B。
5、某单位发当月的工资,已知甲的工资为4500元,若甲取出工资的75%,乙取出工资的1/3,则甲的工资余额是乙的工资余额一半,那么乙当月的工资是多少元?_____
A: 1125B: 3375C: 4500D: 6000
参考答案: B 本题解释:正确答案是B考点和差倍比问题解析甲工资为4500元,取出75%还剩25%,为:4500×25%=1125元,由此乙的工资余额为:1125×2=2250元,占当月的2/3,因此乙当月工资为:2250÷2/3=3375元,故正确答案为B。
6、一个人到书店购买了一本书和一本杂志,在付钱时,他把书的定价中的个位上的数字和十位上的看反了,准备付21元取货。售货员说∶“您应该付39元才对。”请问书比杂志贵多少钱?_____
A: 20B: 21C: 23 0D: 24
参考答案: C 本题解释:【答案】C。解析:数字看反前后,书价相差18,说明十位和个位数字相差为2,总价为39,故书价只能是31,则杂志的价格是8.相差23。
7、银行存款年利率为2.5%,应纳利息税20%,原存1万元1年期,实际利息不再是250元,为保持这一利息收入,应将同期存款增加到_____元。
A: 15000B: 20000C: 12500D: 30000
参考答案: C 本题解释:C。【解析】令存款为x,为保持利息不变,250=x×2.5%×(1-20%)=>x=12500。
8、甲、乙两辆清洁车执行东、西城间的公路清扫任务。甲车单独清扫需要10小时,乙车单独清扫需要15小时,两车同时从东、西城相向开出,相遇时甲车比乙车多清扫12千米,问东、西两城相距多少千米?_____
A: 60B: 50C: 45D: 30
参考答案: A 本题解释:参考答案:A题目详解:根据题意,可知:甲单独清扫需10小时,每小时清扫总路程的 ,乙单独清扫需15小时,每小时清扫总路程的
,乙单独清扫需15小时,每小时清扫总路程的 ,相遇时甲乙一共用时为
,相遇时甲乙一共用时为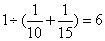 小时;则甲清扫了总路程的
小时;则甲清扫了总路程的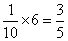 ,乙清扫了总路程的
,乙清扫了总路程的 ,甲比乙多扫了总路程的
,甲比乙多扫了总路程的 ,这一段是12千米,则东、西两城相距为
,这一段是12千米,则东、西两城相距为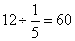 千米。考查点:数量关系>数学运算>行程问题>相遇问题>直线相遇问题>直线一次相遇问题
千米。考查点:数量关系>数学运算>行程问题>相遇问题>直线相遇问题>直线一次相遇问题
9、有一批零件,甲、乙两种车床都可以加工。如果甲车床单独加工,可以比乙车床单独加工提前10天完成任务。现在用甲、乙两车床一起加工,结果12天就完成了任务。如果只用甲车床单独加工需多少天完成任务?_____
A: 20天B: 30C: 40D: 45
参考答案: A 本题解释:参考答案:A题目详解:设甲单独加工x天,乙单独加工 天完成,则甲的工作效率为:
天完成,则甲的工作效率为: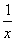 ,乙的工作效率为:
,乙的工作效率为: ;而甲乙合作的效率为:
;而甲乙合作的效率为: ,即:
,即: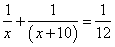 ,解得
,解得 。所以,选A。考查点:数量关系>数学运算>工程问题>单独完工问题
。所以,选A。考查点:数量关系>数学运算>工程问题>单独完工问题
10、已知 对任意的非负整数都成立,且f(1)=2,则
对任意的非负整数都成立,且f(1)=2,则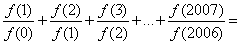 _____
_____
A: 4012B: 4013C: 4014D: 4016
参考答案: C 本题解释:参考答案:C题目详解:根据题意有 即
即 ,故原式=2+2+…+2=2×2007,尾数为4。因此,选C。考查点:数量关系>数学运算>计算问题之算式计算>算式等式问题
,故原式=2+2+…+2=2×2007,尾数为4。因此,选C。考查点:数量关系>数学运算>计算问题之算式计算>算式等式问题
11、4只小鸟飞入4个不同的笼子里去,每只小鸟都有自己的一个笼子(不同的鸟,笼子也不相同),每个笼子只能飞进一只鸟。若都不飞进自己的笼子里去,有多少种不同的飞法?_____。
A: 7B: 8C: 9D: 10
参考答案: C 本题解释:C。本题属于计数问题。本题是排列组合中的错位问题,根据对错位问题数字的记忆,答案应为9种。所以选择C选项。计算过程:设四只小鸟为1,2,3,4,则1有3个笼可选择,不妨假设1进了2号笼,则2也有3个笼可选择,不妨设2进了3号笼,则剩下鸟3、4和笼1、4只有一种选择。所以一共有3×3=9种。
12、100人参加7项活动,已知每个人只参加一项活动,而且每项活动参加的人数都不一样,那么,参加人数第四多的活动最多有几个人参加?_____
A: 22B: 21C: 24D: 23
参考答案: A 本题解释:正确答案是A考点多位数问题解析要保证“第四多的活动越多越好”,那么我们要求"其他活动的人越少越好“,其中有三个比其多,另外三个比其少,比”第四多“的少的最少的就是1、2、3,还剩下100-1-2-3=94,剩下四个活动需要尽量的接近,以保证”第四多“能够尽可能多,所以最好是四个连续的自然数,94÷4=23.5,所以这四个数分别为22、23、24、25,故正确答案为A。
13、有下列长度的三条线段,不能组成三角形的是哪一组?_____
A: 4cm、2cm、5cmB: 12cm、14cm、8cmC: 2cm、3cm、4cmD: 6cm、2cm、3cm
参考答案: D 本题解释:D 【解析】三角形两边之和大于第三边;两边之差小于第三边。
14、有水果糖、奶糖、巧克力三袋重量不同的糖果,水果糖与奶糖的重量比是6:5,若水果糖的2/3被吃掉,且被吃掉的水果糖与被吃掉的巧克力的重量之比是5:4,那么这两种糖剩下的部分重量相等。问原先水果糖、奶糖、巧克力的重量之比是多少?_____
A: 35:30:31B: 25:20:21C: 30:25:26D: 42:35:40
参考答案: C 本题解释:C。
15、当含盐30%的60千克盐水蒸发为含盐40%的盐水时,盐水重量为多少千克?_____
A: 45B: 50C: 55D: 60
参考答案: A 本题解释:【答案】A。解析:根据蒸发前后溶质的质量不变可列方程,设蒸发后盐水质量为x千克,30%×60=40%×x,解得x=45。故选A。
16、四人进行篮球传接球练习,要求每人接球后再传给别人。开始由甲发球,并作为第一次传球,若第五次传球后,球又回到甲手中,则共有传球方式_____。
A: 60种B: 65种C: 70种D: 75种
参考答案: A 本题解释:正确答案:A解析:本题属于排列组合题。我们可以这样想,第n次传球后,球不在甲手中的传球方法,第n+1次传球后,球就可能回到甲手中,所以只需求出第4次传球后,球不在甲手中的传法有多少种。可以列表:从第n次传球、传球的方法、球在甲手中的传球方法、球不在甲手中的传球方法这几个方面进行列表:因为第四次传球不能传给甲,所以本题要分情况讨论:首先,第一次传球甲有3种选择(3),接下来第一种情况:.第二次传球若回到甲手中(1)——第三次传球人有3种选择(3)——第四次传球的人有2种选择,因为不能传给甲(2)。第二种情况:第二次传球没有传给甲(2)——第三次传球传给了甲(1)——第四次传球的人有3种选择(3)。第三种情况:第二次传球没有传给甲(2)——第三次传球也没有传给甲(2)——第四次传球的人有2种选择,因为不能传给甲(2)。综上所述:总传球方式数为3*1*3*2+3*2*1*3+3*2*2*2=60。故答案为A。
17、(2009.江苏C类)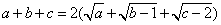 ,则
,则 =_____
=_____
A: 14B: 15C: 3D: 1
参考答案: A 本题解释:参考答案:A题目详解:转换等量关系: ,
,
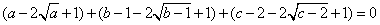
 运算:由于
运算:由于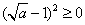 ,
,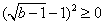 ,
,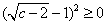 ,故
,故 ,
,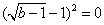 ,
, ,即
,即 ;因此,
;因此,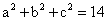 。所以,选A。考查点:数量关系>数学运算>计算问题之算式计算>算式等式问题
。所以,选A。考查点:数量关系>数学运算>计算问题之算式计算>算式等式问题
18、某单位今年一月份购买5包A4纸、6包B5纸,购买A4纸的钱比B5纸少5元;第一季度该单位共购买A4纸15包、B5纸12包,共花费510元。那么每包B5纸的价格比A4纸便宜_____。
A: 1.5元B: 2.0元C: 2.5元D: 3.0元
参考答案: C 本题解释:正确答案是C考点和差倍比问题解析设A4纸和B5纸的价格分别为x元和y元。根据题意可得6y-5x=5,15x+12y=510,解得x=20,y=17.5,那么B5纸的价格比A4纸便宜20-17.5=2.5元。故正确答案为C。
19、从6名男生,5名女生中任选4人参加竞赛,要求男女至少各1名,有多少种不同的选法?_____
A: 240B: 310 C: 720 D: 1080
参考答案: B 本题解释: 答案【B】解析:此题从正面考虑的话情况比较多,如果采用间接法,男女至少各一人的反面就是分别只选男生或者女生,这样就可以变化成C(11,4)-C(6,4)-C(5,4)=310。
20、 _____
_____
A: AB: BC: CD: D
参考答案: B 本题解释:正确答案是B考点和差倍比问题解析将各项直接代入检验,只有B项符合,(21-5)/(29-5)=16/24=2/3,故正确答案为B。标签直接代入
21、同时打开游泳池的A、B两个进水管,加满水需1小时30分钟,且A管比B管多进水180立方米。若单独打开A管,加满水需2小时40分钟。则B管每分钟进水多少立方米?_____
A: 6B: 7C: 8D: 9
参考答案: B 本题解释:由A、B管合作加水90分钟,加满水池且A管比B管多进水180立方米,首先可知A管比B管每分钟多进水2立方米,其次可知若A管自己单独灌水90×2=180(分钟),则也可以灌满水池,且多灌180立方米(此处原理即用A代替B工作,看差异情况),而题中又告知A管单独工作只需160分钟即可灌满水,因此可知多灌的180立方米用时为180—160=20(分钟),因此A管的效率为每分钟9立方米,于是可知B管每分钟进水7立方米。故选B。
22、有一个矩形花园,长比宽多30米,现在花园的四周铺等宽的环路。已知路的面积是800M2,路的外周长是180m,问路宽是多少米?_____
A: 4B: 5C: 6D: 3
参考答案: B 本题解释:【答案】B。解析:设小矩形的宽是x,则长是x+30;设路宽是y,则大矩形的宽是x+2,大矩形的长是x+30+2y,已知条件可表示为(x+2y)(x+30+27)-x(x+30)=800和2(x+2y+x+30+2y)=180,解得y=5米。
23、在一次展览会上,展品上有366部手机不是A公司的,有276部手机不是B公司的,但两公司的展品共有378部。问B公司有多少部手机参展?_____
A: 134B: 144C: 234D: 244
参考答案: C 本题解释:C。其它公司的有(366+276-378)/2=132部,所以B公司有366-132=234,选C。
24、已知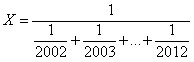 ,问X的整数部分是多少?_____
,问X的整数部分是多少?_____
A: 182B: 186C: 194D: 196
参考答案: A 本题解释:A【解析】由题意可知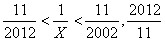 的整数部分是182,
的整数部分是182,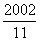 的整数部分也是182,因此X的整数部分也是182。
的整数部分也是182,因此X的整数部分也是182。
25、有四个数,其中每三个数的和分别是45,46,49,52,那么这四个数中最小的一个数是多少_____
A: 12B: 18C: 36D: 45
参考答案: A 本题解释:【答案】A。解析:把四个数加起来,正好相当于把每个人算了3次,因此四人的作品那个岁数为(45+46+49+52)÷3=64,那么年龄最小的为64-52=12岁。
26、二十几个小朋友围成一圈,按顺时针方向一圈一圈地从1开始连续报数,如果报2和200的是同一个人,共有多少个小朋友?_____
A: 26B: 25C: 24D: 22
参考答案: D 本题解释:正确答案是D考点余数与同余问题解析由题干可知,200减去2后是小朋友数的整数倍,即198是正确答案的整数倍。将四个选项带入,只有D符合要求。所以正确答案为D。标签直接代入
27、某城市共有A、B、C、D、E五个区,A区人口是全市人口的5/17,B区人口是A区人口的2/5,C区人口是D区和E区人口总数的5/8,A区比C区多3万人,全市共有多少万人?_____
A: 20.4B: 30.6C: 34.5D: 44.2
参考答案: D 本题解释:正确答案是D考点和差倍比问题解析由A区人口是全市人口的5/17,将全市人口看做17份,则A区有5份,B区有2份,于是C、D、E三区共有10份,而在此三区中,C区人口是D区和E区人口总数的5/8,也即C区人口是此三区人口总数的5/13,因此C区人口为(5/13×10)份,于是A区比C区多5-50/13=15/13份,此部分人口数为3万人,于是全市共有3÷15/13×17=44.2(万人)。故正确答案为D。标签赋值思想
28、一条环形赛道前半段为上坡,后段为下坡,上坡和下坡的长度相等,两辆车同时从赛道起点出发同向行驶,其中A车上、下坡时速相等,而B车上坡时速比A车慢20%,下坡时速比A车快20%,问A车跑到第几圈时两车再次齐头并进?_____
A: 23B: 22C: 24D: 25
参考答案: D 本题解释:正确答案是D考点行程问题解析设A车速度为v,则B车上坡速度为0.8v,B车下坡速度为1.2v。上坡和小坡距离相等,套用等距离平均速度公式可知B车完成一圈的平均速度为(2×0.8v×1.2v)/(0.8v+1.2v)=0.96v。则A车与B车的速度之比为v:0.96v=25:24。也就是说当A车行驶25圈时,B车行驶24圈,此时A、B再次齐头并进,故正确答案为D。标签等距离平均速度模型
29、机床厂有四个车间,其中第二车间的职工数比第一车间人数的2/3多48人,而比第三车间人数的5/4倍少15人,且已知第一车间的人数比第三车间人数多14人,又知第四车间人数占全厂总人数的2/5。机床厂总共有多少人?_____
A: 620B: 670C: 590D: 710
参考答案: B 本题解释:正确答案是B考点和差倍比问题解析
30、每条长200米的三个圆形跑道共同相交于A点,张三、李四、王五三个队员从三个跑道的交点A处同时出发,各取一条跑道练习长跑。张三每小时跑5公里,李四每小时跑7公里,王五每小时跑9公里。问三人第四次在A处相遇时,他们跑了多长时间?_____
A: 40分钟B: 48分钟C: 56分钟D: 64分钟
参考答案: B 本题解释:参考答案B题目详解:他们第四次相遇时:三人跑的路程一定均为200的整数倍;而三个人的速度分别为250/3米/分,350/3米/分,450/3米/分;因此三人第四次相遇时:跑的时间一定是3的整数倍;只有B项符合;所以,选B。考查点:数量关系>数学运算>行程问题>追及问题>环线追及问题>环线多次追及问题
31、某公司去年有员工830人,今年男员工人数比去年减少6%,女员工人数比去年增加5%,员工总数比去年增加3人,问今年男员工有多少人?_____
A: 329B: 350C: 371D: 504
参考答案: A 本题解释:正确答案是A考点和差倍比问题解析设去年男员工X人,女员工Y人,由题意知:X+Y=830,5%Y-6%X=3,解得X=350。今年男员工减少了,所以人数小于350,只有A符合条件,故正确答案为A。秒杀技由题知,今年男员工数是去年的94%,所以今年男员工数可被94%整除,根据选项,只有A符合。故正确答案为A。标签数字特性
32、甲、乙两港相距720千米,轮船往返两港需要35小时,逆流航行比顺流航行多花5小时;帆船在静水中每小时行驶24千米,问帆船往返两港要多少小时?_____
A: 58小时B: 60小时C: 64小时D: 66小时
参考答案: C 本题解释:正确答案是C考点行程问题解析设水流速度为x千米/小时,轮船速度为y千米/小时,根据题意可知,逆流轮船用了20小时,顺流轮船用了15小时,因此有:20(y-x)=720,15(y+x)=720,联立解得x=6,所以帆船往返两港要的时间为:720/(24+6)+720/(24-6)=24+40=64,故选择C选项。标签顺水漂流模型
33、A、B两数恰含有质因数3和5,它们的最大公约数是75,已知A数有12个约数,B数有10个约数,那么,A、B两数的和等于_____。
A: 2500B: 3115C: 2225D: 2550
参考答案: D 本题解释:参考答案 题目详解:由题目可知,A、B两数之和是75的倍数,选项中只有D是75的倍数。考查点:数量关系>数学运算>计算问题之数的性质>公约数与公倍数问题>两个数的最大公约数和最小公倍数
题目详解:由题目可知,A、B两数之和是75的倍数,选项中只有D是75的倍数。考查点:数量关系>数学运算>计算问题之数的性质>公约数与公倍数问题>两个数的最大公约数和最小公倍数
34、王家村西瓜大丰收后,全村男女老少分四个组品尝西瓜,且每组人正好一样,小伙子一个人吃1个,姑娘两个人吃1个,老人三个人吃1个,小孩四个人吃1个,一共吃了200个西瓜,问王家村品尝西瓜的共有_____
A: 368人B: 384人C: 392人D: 412人
参考答案: B 本题解释: B。方法一:利用整除关系。答案必须是2,3,4的公倍挚来源:91考试网 91Exam.org,也就是说答案必须是12的整数倍数。只有B满足。方法二:假设每组有x人。x+x/2+x/3+x/4=200,解得x=96,96×4=384(人)。
35、小伟参加英语考试,共50道题,满分为100分,得60分算及格。试卷评分标准为做对一道加2分,做错一道倒扣2分,结果小伟做完了全部试题但没及格。他发现,如果他少做错两道题就刚好及格了。问小伟做对了几道题?_____
A: 32B: 34C: 36D: 38
参考答案: D 本题解释:正确答案是D考点鸡兔同笼问题解析根据题意,每道题做对与做错相差4分,所以小伟实际得分为60-4×2=52,如果全部做错得-100分,假设小伟做对了n道,则有-100+4n=52,解得n=38道。故正确答案为D。
36、12个啤酒空瓶可以免费换1瓶啤酒,现有101个啤酒空瓶,最多可以免费喝到的啤酒为_____。
A: 10瓶B: 11瓶C: 8瓶D: 9瓶
参考答案: D 本题解释:正确答案是D考点计数模型问题解析根据题意可知,12个空瓶换1瓶酒,12空瓶=1空瓶+1酒,因此题意等价于11空瓶=1酒,而101÷11=9……2,即可换9瓶酒。故答案为D。
37、某学校有一批树苗需要栽种在学院路两旁,每隔5米栽一棵。已知每个学生栽4棵树,则有202棵树没有人栽;每个学生栽5棵树,则有348人可以少栽一棵。问学院路共有多少米?_____
A: 6000 B: 12000 C: 12006 D: 12012
参考答案: A 本题解释:【答案】A。解析:这是个植树问题和盈亏问题的复合问题。植树的学生有(202+348)÷(5-4)=550个,一共栽了550×4+202=2402棵树。每边栽了2402÷2=1201棵树,因此学院路长(1201-1)×5=6000米。
38、小王去一个离家12千米的地方,他每小时步行3千米,每步行50分钟他要休息10分钟,8点整出发,他几点可以到目的地?_____
A: 12点B: 12点30分C: 12点35分D: 12点40分
参考答案: D 本题解释:D。小王不休息的话他走12千米所需的时间是12÷3=4(小时),4小时包含4个50分钟余40分钟,因此小王总共休息了4个10分钟,那么小王花费的总时间是4小时40分钟,也就是小王到达目的地的时间是12点40分。故选D。名师点评:本题很多考生会有如下解法:根据题意每小时中有50分钟行走、10分钟休息,则每个小时小王实际行进2.5千米,因此要步行12千米,用时为12÷2.5=4.8(小时),合4小时48分钟。这是一种典型的错误解法,因为这样相当于取的是等价速度,在整数小时部分不会出现错误,但在非整数部分也即在最后一段,并不是按等价速度来行进的,而是直接行进40分钟到达目的地,而无休息时间。
39、从1、2、3、4、5、6、7、8、9中任意选三个数,使他们的和为偶数,则有多少种选法?_____
A: 40B: 41C: 44D: 46
参考答案: C 本题解释:【答案解析】:选C,形成偶数的情况:奇数+奇数+偶数=偶数;偶数+偶数+偶数=偶数=>其中,奇数+奇数+偶数=偶数=>C(2,5)[5个奇数取2个的种类]×C(1,4)[4个偶数取1个的种类]=10×4=40,偶数+偶数+偶数=偶数=>C(3,4)=4[4个偶数中选出一个不要],综上,总共4+40=44
40、某市园林部门计划对市区内30处绿化带进行补栽,每处绿化带补栽方案可从甲、乙两种方案中任选其中一方案进行。甲方案补栽阔叶树80棵,针叶树40株;乙方案补栽阔叶树50株、针叶树90株。现有阔叶树苗2070株、针对树苗1800株,为最大限度利用这批树苗,甲、乙两种方案要应各选_____。
A: 甲方案18个、乙方案12个B: 甲方案17个、乙方案13个C: 甲方案20个、乙方案10个D: 甲方案19个、乙方案11个
参考答案: A 本题解释:正确答案是A考点统筹规划问题解析假定甲方案X个、乙方案Y个,根据题意:X+Y=30,80X+40Y≤2070,50X+90Y≤1800,并使得数字越接近2070和1800越好。可直接将选项代入验证。首选甲方案或乙方案最多的两个极端情况(极端情况很有可能不符合而被排除),若为C,则80×20+50×10=2100>2070,排除;若为B,则80×17+50×13=1910>1800,排除。若为A,阔叶树用80×18+50×12=2040株,针叶树40×18+90×12=1800株,剩余30株;若为D,阔叶树用80×19+50×11=2070株,针叶树40×19+90×11=1750株,剩余50株。故正确答案为A。
41、(2009黑龙江)甲、乙两人从两地出发相向而行,他们在相遇后继续前行。当甲走完全程的70%时,乙正好走完全程的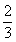 ,此时两人相距220米,问两地相距多少米?_____
,此时两人相距220米,问两地相距多少米?_____
A: 3360米B: 6圈C: 3320米D: 6圈340米
参考答案: B 本题解释:参考答案 题目详解:甲、乙第一次相遇时共跑0.5圈,乙跑了100米;第二次相遇时,甲、乙共跑1.5圈,则乙跑了100×3=300米,此时甲差60米跑一圈,则可得0.5圈是300-60=240米,一圈是2×240=480米。第一次相遇时甲跑了240-100=140米,以后每次相遇甲又跑了140×2=280米,所以第十二次相遇时甲共跑了140+280×11=3220=6圈340米。考查点:数量关系>数学运算>行程问题>相遇问题>环线相遇问题>环线多次相遇问题
题目详解:甲、乙第一次相遇时共跑0.5圈,乙跑了100米;第二次相遇时,甲、乙共跑1.5圈,则乙跑了100×3=300米,此时甲差60米跑一圈,则可得0.5圈是300-60=240米,一圈是2×240=480米。第一次相遇时甲跑了240-100=140米,以后每次相遇甲又跑了140×2=280米,所以第十二次相遇时甲共跑了140+280×11=3220=6圈340米。考查点:数量关系>数学运算>行程问题>相遇问题>环线相遇问题>环线多次相遇问题
42、一种溶液,蒸发掉一定量的水后,溶液的浓度为10%;再蒸发掉同样多的水后,溶液的浓度变为12%;第三次蒸发掉同样多的水后,溶液的浓度将变为多少?_____
A: 14%B: 17%C: 16%D: 15%
参考答案: D 本题解释:正确答案是D考点浓度问题解析在蒸发的过程中,溶液的量发生变化,但其中溶质保持不变,因此将溶质作为解题突破口,给溶质赋值。为方便后面的计算,设其溶质为60,则可知其浓度在10%时,溶液量为600,其浓度在12%时,溶液量为500。这说明在变化过程中蒸发掉了水为100。因此第三次蒸发同样多的水后,溶液还剩400,故其浓度为15%。故正确答案为D。标签赋值思想
43、如果一个三角形的底边长增加10%,底边上的高缩短10%,那么这个新三角形的面积是原来三角形面积的_____。
A: 90%B: 80%C: 70%D: 99%
参考答案: D 本题解释:D解析:设原三角形底边为a,高为h,面积为S,则得:S=1/2ah。那么新三角形S新=1/2a(1+10%)?h(1-10%)=1/2?ah×99%=99%S,故答案为D。
44、小华在练习自然数求和,从1开始,数着数着他发现自己重复数了一个数。在这种情况下,他将所数的全部数求平均,结果为7.4,请问他重复的那个数是_____。
A: 2B: 6C: 8D: 10
参考答案: B 本题解释:正确答案是B考点平均数问题解析 故正确答案为B。秒杀技总和=7.4×总个数,总和是整数,故总个数肯定是5的倍数。由于平均数是7.4,所以总个数应该是10或者15。如果总个数是10,总和应该是74,由于从1到10加起来才55,说明肯定不是10。总个数是15,总和应该是7.4×15=111,而从1到14加起来是(1+14)×14÷2=105,说明多加了一个6。故正确答案为B。标签数字特性
故正确答案为B。秒杀技总和=7.4×总个数,总和是整数,故总个数肯定是5的倍数。由于平均数是7.4,所以总个数应该是10或者15。如果总个数是10,总和应该是74,由于从1到10加起来才55,说明肯定不是10。总个数是15,总和应该是7.4×15=111,而从1到14加起来是(1+14)×14÷2=105,说明多加了一个6。故正确答案为B。标签数字特性
45、小明前三次数学测验的平均分数是88分,要想平均分数达到90分以上,他第四次测验至少要达到_____
A: 98分B: 96分C: 94分D: 92分
参考答案: B 本题解释: 【解析】B。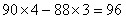 分,该数值可以根据以上式子判定尾数为6,选择B。
分,该数值可以根据以上式子判定尾数为6,选择B。
46、某运输队有大货车和小货车24辆,其中小货车自身的重量和载货量相等,大货车的载货量是小货车的1.5倍,自身重量是小货车的2倍。所有车辆满载时共重234吨,空载则重124吨,那么该运输队的大货车有多少辆? _____
A: 4B: 5C: 6D: 7
参考答案: D 本题解释:D【解析】设大货车数量为x,小货车自重量为a,小货车数量为24-x,列方程x?2a+(24-x)?a=124[x?2a+(24-x)?a]+x?1 5a+(24-x)?a=234 解得x=7。故选D。
47、(2009天津、湖北、陕西联考,第95题)有4支队伍进行4项体育比赛,每项比赛的第一、第二、第三、第四名分别得到5,3,2,1分,每队的4项比赛的得分之和算作总分,如果已知各队的总分不相同,并且A队获得了三项比赛的第一名,问总分最少的队伍最多得多少分?_____
A: 7B: 8C: 9D: 10
参考答案: B 本题解释:参考答案:B题目详解:本题需要运用“构造法”和“极端法”。由于题目求“总分最少的队伍最多得多少分”,我们需要让各队的得分尽可能的平均。每项比赛产生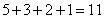 分,4项比赛一共产生
分,4项比赛一共产生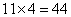 分,最终平均每人得到
分,最终平均每人得到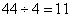 分。A已经获得了
分。A已经获得了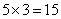 分,超过平均分,需要A最后=场比赛得尽量少的分,即1分,那么剩下3个人将得到
分,超过平均分,需要A最后=场比赛得尽量少的分,即1分,那么剩下3个人将得到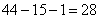 分。要让剩下三个人比分尽可能的平均,可以构造
分。要让剩下三个人比分尽可能的平均,可以构造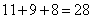 ,在这个条件下,部分最少的队伍可以得到最多的分数,即8分。下面我们构造这种比赛的情形:
,在这个条件下,部分最少的队伍可以得到最多的分数,即8分。下面我们构造这种比赛的情形: 考查点:数量关系>数学运算>排列组合问题>比赛问题>循环赛
考查点:数量关系>数学运算>排列组合问题>比赛问题>循环赛
48、三个连续的偶数的乘积为192,那么其中最大的数是多少?_____
A: 4B: 6C: 12D: 8
参考答案: D 本题解释:答案:D【解析】设最小的偶数为x,则这三个偶数依次为x,x+2,x+4,故x?(x+2)?(x+4)=192。用代入法解答。经过验证x=4,则最大的偶数为8。因此正确答案为D。
49、两个圆柱形水井,甲井的水深是乙井的一半,水面直径是乙井的2倍,蓄水量为40立方米,问乙井的蓄水量为多少立方米?_____
A: 20B: 40C: 60D: 80
参考答案: A 本题解释:正确答案是A考点几何问题解析甲井水面直径是乙井的2倍,则水面面积是乙井的4倍,而水深为乙井的一半,因此甲井蓄水体积是乙井的2倍,因此乙井的蓄水量是:40÷2=20立方米,故正确答案为A。
50、一个长方体的长、宽、高恰好是三个连续的自然数,并且它的体积数值等于它的所有棱长之和的2倍,那么这个长方体的表面积是_____
A: 74B: 148C: 150D: 154
参考答案: B 本题解释:【解析】B。设该长方体的长、宽、高分别是 。那么有
。那么有 所以这个长方体的表面积为
所以这个长方体的表面积为
51、气象台测得在S岛正东方向80千米处,一台风中心正以20千米/小时的速度沿北偏西60度的方向匀速移动。若台风中心50千米范围内为影响区域,台风中心移动方向不变、强度不变,该台风对S岛的影响时间约持续_____。
A: 2小时B: 3小时C: 4小时D: 5小时
参考答案: B 本题解释:正确答案是B考点几何问题解析 故正确答案为B。
故正确答案为B。
52、有a、b、c、d四条直线,依次在a线上写1,在b线上写2,在c线上写3,在d线上写4,然后在a线上写5,在b线、c线和d线上写数字6,7,8…按这样的周期循环下去,问数字2007在哪条线上?_____
A: a线B: b线C: c线D: d线
参考答案: C 本题解释:正确答案是C考点周期问题解析该循环以4为周期,2007÷4=501余3,那么2007应该标在c线上,故正确答案为C
53、(2004广东)两艘渡轮在同一时刻垂直驶离H河的甲、乙两岸相向而行,一艘从甲岸驶向乙岸,另一艘从乙岸开往甲岸,它们在距离较近的甲岸720米处相遇。到达预定地点后,每艘船都要停留10分钟,以便让乘客上船下船,然后返航。这两艘船在距离乙岸400米处又重新相遇。问:该河的宽度是多少?_____
A: 1120米B: 1280米C: 1520米D: 1760米
参考答案: D 本题解释:参考答案 题目详解:如下图所示,设从甲、乙两岸出发的船分别为A船、B船,全程为x米,则:
题目详解:如下图所示,设从甲、乙两岸出发的船分别为A船、B船,全程为x米,则: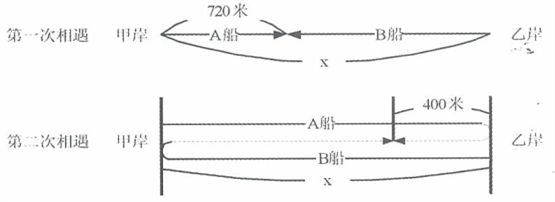 从出发到第一次相遇时,A船行驶了720米,B船行驶了
从出发到第一次相遇时,A船行驶了720米,B船行驶了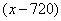 米;从出发到第二次相遇时,A船行驶了
米;从出发到第二次相遇时,A船行驶了 米,B船行驶了
米,B船行驶了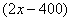 米;注意到两船靠岸后停靠时间相同,从出发到第一次相遇及从出发到第二次相遇两船运动时间对应相等。根据“时间一定的情况下,速度和路程成正比”,我们可以得到:
米;注意到两船靠岸后停靠时间相同,从出发到第一次相遇及从出发到第二次相遇两船运动时间对应相等。根据“时间一定的情况下,速度和路程成正比”,我们可以得到: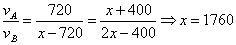 (米)因此,选D。注释:设第一次相遇地点距离甲岸
(米)因此,选D。注释:设第一次相遇地点距离甲岸 ,第二次相遇地点距离乙岸
,第二次相遇地点距离乙岸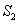 ,则:
,则: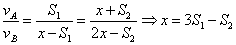 考查点:数量关系>数学运算>行程问题>相遇问题>直线相遇问题>直线多次相遇问题
考查点:数量关系>数学运算>行程问题>相遇问题>直线相遇问题>直线多次相遇问题
54、一批布料,全部用来做上衣可做60件,全部用来做裤子可做40条,现在做上衣、裤子、裙子各5件,恰好用去全部布料的1/4,剩下布料全部做裙子,则还可以做多少条?_____
A: 80B: 90C: 100D: 110
参考答案: B 本题解释:B【解析】设布料总量为120单位,则每件上衣需2单位布料,每条裤子需3单位布料,又上衣、裤子、裙子各做5件,用去︰120×1/4=30单位,所以每条裙子需1单位布料,则可再生产裙子︰(l20-30)÷1=90(条),故答案为B选项。
55、有一工作,甲做2天后乙接着做,做了10天后完成了工作。已知乙单独完成需要30天,那么甲单独完成此工作需要_____天。
A: 3天B: 1天C: 10天D: 2天
参考答案: A 本题解释:【答案解析】由题可知,甲做2天,相当于乙做20天,则乙做30天的工作,甲3天即可完成。
56、连接正方体每个面的中心构成一个正八面体(如下图所示)。己知正方体的边长为6厘米,问正八面体的体积为多少立方厘米?_____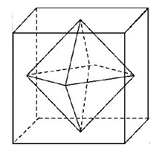
A: 182B: 242C: 36D: 72
参考答案: C 本题解释:正确答案是C考点几何问题解析正八面体可以拆解成两个完全相同的四棱锥,每个棱锥的体积V=1/3Sh,高度h为正方体边长的一半,h=3厘米,棱锥的底面是下面正方体横截面(从正中切开)里的小正方形,因此棱锥的底面积是正方体底面积的一半:6×6÷2=18平方厘米,每个棱锥的体积为1/3×18×3=18立方厘米,该正八面体的体积为18×2=36立方厘米,故正确答案为C。
57、甲、乙两个冷藏库共存鸡蛋6250箱,先从甲库运走1100箱后,这时乙库存的鸡蛋比甲库剩下的2倍还多350箱,求甲库比乙库原来少存了鸡蛋多少箱?_____
A: 550B: 650C: 750D: 850
参考答案: D 本题解释:参考答案 题目详解:根据题意,可知:甲库运走l100箱以后,则:两库还剩下:6250-1100=5150箱,甲库还剩下:(5150-350)÷(1+2)=1600箱;那么,则有:甲库原存鸡蛋为:1600+1100=2700箱,乙库原来存鸡蛋为:1600×2+350=3550箱,甲库比乙库少:3550-2700=850箱。考查点:数量关系>数学运算>和差倍比问题>和差倍问题
题目详解:根据题意,可知:甲库运走l100箱以后,则:两库还剩下:6250-1100=5150箱,甲库还剩下:(5150-350)÷(1+2)=1600箱;那么,则有:甲库原存鸡蛋为:1600+1100=2700箱,乙库原来存鸡蛋为:1600×2+350=3550箱,甲库比乙库少:3550-2700=850箱。考查点:数量关系>数学运算>和差倍比问题>和差倍问题
58、把一根钢管锯成两段要用4分钟,若将它锯成8段要多少分钟?_____
A: 16B: 32C: 14D: 28
参考答案: D 本题解释:参考答案 题目详解:根据题意,可知:此钢管锯一次要用4分钟,那么将它锯成8段要锯7次需要7×4=28分钟。所以,选D。注:本题的前提是不能叠在一起锯,叠在一起时间应该会更长。考查点:数量关系>数学运算>特殊情境问题>植树问题>两端均不植树
题目详解:根据题意,可知:此钢管锯一次要用4分钟,那么将它锯成8段要锯7次需要7×4=28分钟。所以,选D。注:本题的前提是不能叠在一起锯,叠在一起时间应该会更长。考查点:数量关系>数学运算>特殊情境问题>植树问题>两端均不植树
59、用6位数字表示日期,如980716表示的是1998年7月16日。如果用这种方法表示2009年的日期,则全年中六个数字都不相同的日期有多少天?_____
A: 12B: 29D: 1
参考答案: C 本题解释:正确答案是C考点多位数问题解析根据题目条件,显然要知道有多少个符合要求的日期,只需实际构造即可,而在构造的过程中,显然顺序是先安排月份,再安排具体日期。假设2009年AB月CD日,满足要求,它可以简写成“09ABCD”,由于月份当中不能有0,所以不能是01—10月,而11月有两个1,也应该排除,故AB=12;此时原日期可简写成“0912CD”,由于已经出现了0、1、2,所以肯定不是01—30号,而31号里又有1了,排除,因此满足题目要求的日期为0个,故正确答案为C。标签构造调整
60、自行车和三轮车合计31辆,这31辆车共有76个轮子,问自行车、三轮车各有多少辆?_____
A: 16,15B: 17,14C: 18,13D: 19,12
参考答案: B 本题解释:参考答案:B题目详解:假设全是三轮车,可得:自行车有: 辆,三轮车有:
辆,三轮车有: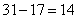 辆。所以,选B。考查点:数量关系>数学运算>特殊情境问题>鸡兔同笼问题>鸡兔同笼变形问题
辆。所以,选B。考查点:数量关系>数学运算>特殊情境问题>鸡兔同笼问题>鸡兔同笼变形问题
61、动物园的饲养员给三群猴子分花生,如只分给第一群,则每只猴子可得12粒;如只分给第二群,则每只猴子可得15粒;如只分给第三群,则每只猴子可得20粒,那么平均分给三群猴子.每只可得多少粒?_____
A: 3B: 4C: 5D: 6
参考答案: C 本题解释:参考答案:C题目详解:解法一:此题用特值法:设花生有60粒;那么第一群有 只猴子;第二群有
只猴子;第二群有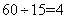 只猴子;第三群有
只猴子;第三群有 只猴子;三群一共有的猴子数量为:
只猴子;三群一共有的猴子数量为: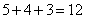 只,因此每只可以分到
只,因此每只可以分到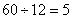 粒;所以,选C。解法二:由题意可知:花生总数必定是12、15、20的倍数。采用设数法:假设共有花生
粒;所以,选C。解法二:由题意可知:花生总数必定是12、15、20的倍数。采用设数法:假设共有花生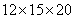 粒;那么第一群猴子有
粒;那么第一群猴子有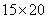 只;第二群猴子有
只;第二群猴子有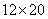 只;第三群猴子有
只;第三群猴子有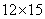 只;即共有的猴子数量为:
只;即共有的猴子数量为: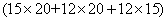 只;
只; ;所以平均分给三群猴子,每个猴子可得5粒。所以,选C。考查点:数量关系>数学运算>计算问题之算式计算>平均值问题>算术平均值
;所以平均分给三群猴子,每个猴子可得5粒。所以,选C。考查点:数量关系>数学运算>计算问题之算式计算>平均值问题>算术平均值
62、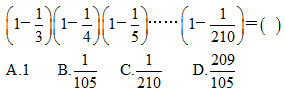 _____
_____
A: AB: BC: CD: D
参考答案: B 本题解释:正确答案是B解析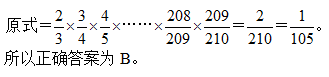 考点计算问题
考点计算问题
63、在某企业,40%的员工有至少3年的工龄,16个员工有至少8年的工龄。如果90%的员工的工龄不足8年,则工龄至少3年但不足8年的员工有_____人。
A: 48B: 64C: 80D: 144
参考答案: A 本题解释:正确答案是A考点和差倍比问题解析通过题干可知,工龄大于8年的占(1-90%)=10%,而这部分有16人,则共有工人160人,同时,通过题干可知,工龄大于3年小于8年的员工为至少3年的员工数减去至少8年的员工数,为160×40%-16=48人,故正确答案为A。
64、将700克14.3%的盐水与900克11.1%的盐水混合后,再加入200克盐,蒸发掉300克水后,该盐水的浓度为_____。
A: 22.2%B: 24.3%C: 26.7%D: 28.6%
参考答案: C 本题解释:【答案】C。解析:由题意可得,最后该盐水浓度为(700×14.3%+900×11.1%+200)÷(700+900+200-300)=400÷1500≈26.7%。故正确答案为C。
65、早上7点两组农民开始在麦田里收割麦子,其中甲组20人,乙组15人。8点半,甲组分出10个人捆麦子;10点,甲组将本组所有已割的麦子捆好后,全部帮乙组捆麦子;如果乙组农民一直在割麦子,什么时候乙组所有已割麦子能够捆好?(假设每个农民的工作效率相同)_____
A: 10:45B: 11:00C: 11:15D: 11:30
参考答案: B 本题解释:正确答案是B考点工程问题解析采用赋值思想,设每个农民割麦子的效率为1,由题意可得,甲组割麦子的总量为20×1.5+10×1.5=45,故每个农民捆麦子的效率为45÷1.5÷10=3;设从10点之后经过n小时,乙组的麦子全部捆好。故乙组割麦子的总量为15×(3+n),捆麦子总量为20×3×n,两值应相等,即45+15n=60n,解得n=1,即再过1小时就全部捆好了,此时为11:00。故正确答案为B。标签赋值思想
66、用2、3、4、5、6、7六个数字组成两个三位数,每个数字只用一次,这两个三位数的差最小是多少?_____
A: 47B: 49C: 69D: 111
参考答案: A 本题解释:正确答案是A考点多位数问题解析因为每个数字只能用一次,显然首位决定大小,因此三个三位数的百位数字至少相差1,在这种情况下要使差值最小,则两个三位数为最接近,从而可知较小的三位数之末两位应尽可能大,而较大的三位数之末两位应尽可能小。在这个思想下,可知合适的三位数情况构造为523、476,此时三位数之末两位的差距最大,从而差值最小,最小差值为47。故正确答案为A。
67、100张多米诺骨牌整齐地排成一列,依顺序编号为1、2、3……99,100.第一次拿走所有奇数位置上的骨牌,第二次再从剩余骨牌中拿走所有奇数位置上的骨牌,依此类推。请问最后剩下的一张骨牌的编号是多少?_____
A: 32 B: 64 C: 88 D: 96
参考答案: B 本题解释:【解析】本题关键是理解题意,第一次拿走的是所有奇数,第二次拿走的各项是2分别乘以1、3、5、7、9……,依次类推,每拿走一次后,剩下的第一个数是20、21,22、23、24……,在100之内要使2n取值最大,所以最后剩下的是64,选B.
68、如图所示,△ABC是直角形,四边形IBFD和四边形HFGE都是正方形,已知AI=1cm,IB=4cm,正方形HFGE的面积是_____。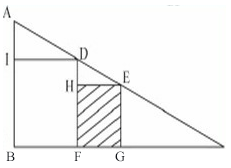
A: AB: BC: CD: D
参考答案: C 本题解释:正确答案是C考点几何问题解析设正方形HFGE的边长为X,由三角形EHD相似于三角形DIA可知,EH/DH=DI/DA,即X/(4-X)=4/1,解得X=16/5,那么正方形面积为16/5×16/5=10.24,故正确答案为C。
69、单独完成某项工作,甲需要16小时,乙需要12小时,如果按照甲、乙、甲、乙……的顺序轮流工作,每次1小时,那么完成这项工作需要多长时间?_____
A: 13小时40分钟B: 13小时45分钟C: 13小时50分钟D: 14小时
参考答案: B 本题解释:答案:B.[解析]本题为工程类题目。设总工程量为48,则甲的效率是3,乙的效率是4,工作12小时后,完成了42。第12小时甲做了3,完成了总工程量45,剩余的3由乙在第十四小时完成。在第十四小时里,乙所用的时间是3/4小时,所以总时间是13.75小时。
70、小王的手机通讯录上有一手机号码,只记下前面8个数字为15903428。但他肯定,后面3个数字全是偶数,最后一个数字是6,且后3个数字中相邻数字不相同,请问该手机号码有多少种可能?_____
A: 15B: 16C: 20D: 18
参考答案: B 本题解释:答案:B【解析】一位偶数有0、2、4、6、8,共5个。考虑倒数第二位,因为相邻数字不相同且为偶数,则有4种选择。倒数第三位与倒数第二位不相同,也有4种选择,共有4×4=16种情况。
71、8点28分,时钟的分针与时针的夹角(小于180)是多少度?_____
A: 86B: 87C: 88D: 89
参考答案: A 本题解释:参考答案:A题目详解:8点整时:时针的度数为240°;经过28分钟:该夹角为240-(6-0.5)×28=86度;所以,选A。考查点:数量关系>数学运算>特殊情境问题>钟表问题>时针与分针的角度关系
72、甲乙两人参加射击比赛,规定每中一发记5分,脱靶一发倒扣3分。两人各打了10发子弹后,分数之和为52,甲比乙多得了16分。问甲中了多少发?_____
A: 9B: 8C: 7D: 6
参考答案: B 本题解释:正确答案是B考点鸡兔同笼问题解析甲和乙的分数之和是52,分数之差是16,那么甲的分数是(52+16)÷2=34分,要是甲10发全部打中,则应该得50分,由差异分析可知,甲脱靶的发数为(50-34)÷(5+3)=2发,所以打中的发数为10-2=8发。因此正确答案为B。
73、除以5余1,b除以5余4,如果3a >b,那么3a-b除以5余几? _____
A: 1B: 2C: 3D: 4
参考答案: D 本题解释:D【解析】3a 除以5 应余1×3=3,已知b 除以5 余4,则3a-b 除以5 余3-4+5=4。故选D。
74、三位数的自然数P满足:除以7余2,除以6余2,余以5也余2,则符合条件的自然数P有_____。
A: 2个B: 3个C: 4个D: 5个
参考答案: C 本题解释:正确答案是C考点余数与同余问题解析解析1:由题可知,该数减去2应当同时为5、6、7的倍数,5、6、7的最小公倍数为210,故满足条件的三位数有210+2=212,210×2+2=422,210×3+2=632,210×4+2=842,共四个数字。故正确答案为C。解析2:根据口诀:余同取余,和同加和,差同减差,最小公倍数做周期。知道满足余同,该自然数P满足P=210n+2,又P是三位数,则100≤210n+2≤999,解得:1≤n≤4。满足条件的n有4个。故正确答案为C。标签最小公倍数
75、某工厂的一个生产小组,当每个工人都在岗位工作时,9小时可以完成一项生产任务。如果交换工人甲和乙的岗位,其他人不变,可提前1小时完成任务;如果交换工人丙和丁的岗位,其他人不变,也可提前1小时完成任务。如果同时交换甲和乙、丙和丁的岗位,其他人不变,可以提前多少小时完成这项任务?_____
A: 1.4B: 1.8C: 2.2D: 2.6
参考答案: B 本题解释:正确答案是B考点工程问题解析交换甲和乙或丙和丁的工作岗位,均可8小时完成任务,说明交换甲和乙或丙和丁,整体工作效率由1/9变为1/8,提高了1/72。则同时交换甲乙、丙丁,整体效率提高了1/36,则效率由1/9变成1/9+1/36=5/36,于是完成用时36/5=7.2(小时),提前了1.8小时完成。故正确答案为B。
76、有面值为8分、1角和2角的三种纪念邮票若干张,总价值为1元2角2分,则邮票至少有_____。
A: 7张B: 8张C: 9张D: 10张
参考答案: C 本题解释:C【解析】要使邮票最少,则要尽量多的使用大面额邮票,所以要达到总价值,2角的邮票要使用4张,1角的邮票要使用1张,8分的邮票要4张,这样使总价值正好为1元2角2分,所以要用9张。
77、如果a△b表示(a-2)×b,例如3△4=(3-2)×4=4,那么,当a△5=30时,a=_____。
A: 5B: 6C: 8D: 11
参考答案: C 本题解释:参考答案:C题目详解:根据题意可知(a-2)×5=30,解得a=8,所以,选C。考查点:数量关系>数学运算>计算问题之算式计算>定义新运算问题
78、5人参加一次小测验,试卷上的10道题目均为4选1的单项选择题,若5个人全部答完所有题目,那么不同的答卷最多有_____种。
A: 410B: 510C: 40D: 200
参考答案: A 本题解释:A【解析】从第1题开始最多可能出现4种不同的答案,然后在做第2题时也可能有4种不同的答案,直到第10题依然会出现4种答案。符合排列组合中乘法原理,因此不同的答卷一共会出现:4×4×4×…×4=410(种)。故答案为A。
79、一袋白糖,第一次用去0.3斤,第二次用去余下的3/4,这时袋内还有白糖0.2斤,该袋糖原有多少斤?_____
A: 1.1B: 0.5C: 1.5D: 2
参考答案: A 本题解释: A 【解析】0.2÷(1-3/4)+0.3=1.1。
80、运送一批货物总运费为4200元,A、B两家运输公司同时运送8小时完成,A公司单独运输需14小时完成。现由A公司单独运送若干小时后,再由B公司单独运送剩下的货物。这样共用18小时全部运完。那么A、B两公司应分别获得:_____
A: 2100元,2100元B: 600元,3600元C: 1400元,2800元D: 800元,3400元
参考答案: A 本题解释:A。每小时是300,所以排除CD(都不是300的倍数),B每小时是4200/8-300=225,排除A(不是225倍数),所以选B。
81、如下图所示,△ABC中DE∥BC,且BO和CO分别是∠ABC和∠ACB的角平分线。已知AB=25.4cm,BC=24.5cm,AC=20cm。问△ADE的周长是多少?_____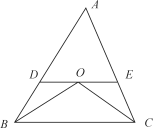
A: 45.4cmB: 45.1cmC: 44.8cmD: 44.5cm
参考答案: A 本题解释:正确答案是A考点几何问题解析BO是∠ABC的角平分线,则∠ABO=∠OBC,又DE∥BC,得∠OBC=∠BOD,因此△BOD是等腰三角形,有BD=OD,同理有CE=OE,因此△ADE的周长=AD+AE+DE=AB+AC=45.4(cm)。标签画图分析
82、一笔奖金分一等奖、二等奖和三等奖,每个一等奖的奖金是每个二等奖奖金的两倍,每个二等奖的奖金是每个三等奖奖金的两倍。如果评一、二、三等奖各两人,那么每个一等奖金是308元;如果评一个一等奖,三个三等奖,两个二等奖,那么一等奖的奖金是多少元_____
A: 154B: 196C: 392D: 490
参考答案: C 本题解释:【答案解析】①每个二等奖奖金为:308÷2=154(元)。②每个三等奖奖金为:154÷2=77(元)。③一共有奖金:(308+154+77)×2=1078(元)。④设一个三等奖奖金为x元,则一个二等奖奖金为2x元,一个一等奖奖金为4x元,列方程得:4x+4x+3x=1078,x=98。一等奖奖金为:98×4=392(元)。故正确答案为C。
83、把自然数按由小到大的顺序排列起来组成第一串数:1、2、3、……、9、10、11、12、……把这串数中两位以上的数全部隔开成一位数字,组成第二串数:1、2、……、9、1、0、1、1、1、2、1、3、……。则第一串数中100的个位数字0在第二串数中是第几个数?_____
A: 188B: 198C: 192D: 202
参考答案: C 本题解释:正确答案是C考点多位数问题解析根据题意,第一串数一位数(1—9)有9个,可分成9个数字;两位数(10—99)有99-10+1=90个,可分成90×2=180个数,则第一串数中100的个位数0在第二串数字中的位置为9+180+3=192,故正确答案为C。
84、定义4△5=4+5+6+7+8=30,7△4=7+8+9+10=34,按此规律,(26△15)+(10△3)的值为_____。
A: 528B: 525C: 423D: 420
参考答案: A 本题解释:正确答案是A考点计算问题解析三角符号代表着以符号前一个数为首项,符号后的数为项数,公差为1的一个等差数列,用等差公式求和,26△15=26+…+40=(26+40)×15÷2=495,10△3=10+11+12=33,因此和值为528。故答案为A。
85、甲容器中有浓度为4%的盐水150克,乙容器中有某种浓度的盐水若干,从乙中取出450克盐水,放入甲中混合成浓度为8.2%的盐水。问乙容器中盐水的浓度是多少?_____
A: 9.6%B: 9.8%C: 9.9%D: 10%
参考答案: A 本题解释:正确答案是A考点浓度问题解析解析1: 解析2:设乙浓度为C,由十字交叉法得甲、乙质量之比为(C-8.2%):(8.2%-4%)=150:450,解得C=9.6%,故正确答案为A。
解析2:设乙浓度为C,由十字交叉法得甲、乙质量之比为(C-8.2%):(8.2%-4%)=150:450,解得C=9.6%,故正确答案为A。
86、一汽船往返于两码头间,逆流需要10小时,顺流需要6小时。已知船在静水中的速度为12公里/小时。问水流的速度是多少公里/小时?_____
A: 2B: 3C: 4D: 5
参考答案: B 本题解释:正确答案是B考点计数模型问题解析根据顺水漂流模型公式:(船速+水速)×顺水时间=(船速-水速)×逆水时间,可得(12+水速)×6=(12-水速)×10,解得水速=3,故正确答案为B。标签顺水漂流模型
87、将5封信投入3个邮筒,不同的投法共有_____。
A: 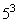 种B:
种B: 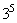 种C: 3种D: 15种
种C: 3种D: 15种
参考答案: B 本题解释:参考答案:B题目详解:5封信投入3个信箱:每封信面对3个邮箱,都会有3种选择,且每次投信是独立的,不互相影响;根据排列组合中相乘原理的概念: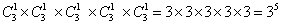 ;所以,选B。考查点:数量关系>数学运算>排列组合问题>常规排列组合问题
;所以,选B。考查点:数量关系>数学运算>排列组合问题>常规排列组合问题
88、某人在公共汽车上发现一个小偷向相反方向步行,10秒钟后他下车去追小偷,如果他的速度比小偷快一倍,比汽车慢,则此人追上小偷需要_____。
A: 20秒B: 50秒C: 95秒D: 110秒
参考答案: D 本题解释:D【解析】设某人速度为v,则小偷速为0.5v,汽车速为5v,10秒钟内,与小偷相差(0.5+5)v×10=55v,追求时速差为0.5v,所以所需时间为110秒。
89、某种型号拖拉机,前轮直径为50厘米,后轮直径为150厘米,拖拉机前进时,前轮转了240圈,求后轮转了多少圈?_____
A: 60B: 40C: 30D: 80
参考答案: D 本题解释:【解析】D。圆的周长与其直径成正比。
90、有5个数的算术平均数为25,去掉其中一个数后,算术平均数为31,试问去掉的那个数是多少?_____
A: 4B: 3C: 1D: 2
参考答案: C 本题解释:参考答案:C题目详解:解法一: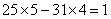 (尾数法)。解法二:依题意:设去掉的那个数为
(尾数法)。解法二:依题意:设去掉的那个数为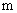 ,剩余四个数和为
,剩余四个数和为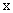 ;则5个数之和为25,可得:
;则5个数之和为25,可得: ;则去掉一个数
;则去掉一个数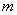 之后平均值:
之后平均值: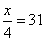 ,解方程得:
,解方程得: ;所以,选C。考查点:数量关系>数学运算>计算问题之算式计算>平均值问题>算术平均值
;所以,选C。考查点:数量关系>数学运算>计算问题之算式计算>平均值问题>算术平均值
91、用分期付款的形式还贷,贷款1万元,3年还清,每月应还301.914元,那么贷款60万元,3年还清,每期应还_____。
A: 1666.67元B: 1811.484元C: 18666.67元D: 18114.84元
参考答案: D 本题解释:正确答案是D考点和差倍比问题解析1万元,3年还清,每月应还301.914元,那么60万元,3年还清,每月应还金额为301.914×60,尾数为4,排除A、C。利用估算法得301.914×60≈300×60=18000,故正确答案为D。标签尾数法
92、A、B两站之间有一条铁路,甲、乙两列火车分别停在A站和B站,甲火车4分钟走的路程等于乙火车5分钟走的路程,乙火车上午8时整从B站开往A站,开出一段时问后,甲火车从A站出发开往B站,上午9时整两列火车相遇,相遇地点离A、B两站的距离比是15:16,那么,甲火车在什么时刻从A站出发开往B站?()
A: 8时12分B: 8时15分C: 8时24分D: 8时30分
参考答案: B 本题解释:正确答案是B考点行程问题解析
93、某人以八五折的优惠购买一辆自行车节省60元,他实际付款_____元。
A: 350B: 380C: 400D: 340
参考答案: D 本题解释:正确答案是D考点经济利润问题解析根据题意,自行车的原价为:60÷15%=400,所以实际付款额为:400-60=340元。故正确答案为D。
94、在某状态下,将28克某种溶质放入99克水中,恰好配成饱和溶液。从中取出1/4溶液,加入4克溶质和11克水,请问此时浓度变为多少?_____
A: 21.61%B: 22.05%C: 23.53%D: 24.15%
参考答案: B 本题解释:正确答案是B考点浓度问题解析本题需要注意判断溶液的浓度,首先要判断溶液是否饱和。由于99克水最多可以溶解28克溶质,则11克水最多可以溶解28/9克溶质,即小于4克溶质,因此饱和溶液加入4克溶质和11克水仍为饱和溶液,故饱和溶液浓度为:28/(28+99)×100%≈22.05%,故正确答案为B。
95、2004年2月28日是星期六,那么2010年2月28日是_____。
A: 星期一B: 星期三C: 星期五D: 星期日
参考答案: D 本题解释:正确答案是D考点星期日期问题解析2004年2月28日到2010年2月28日之间隔了6年,一年365天是52个星期加1天,因此过6年的星期变化相当于过6天。而2004年、2008年是闰年,要各多加1天。因此,2010年2月28日的星期数相当于从周六开始向后再过8天,应为星期日。故正确答案为D。
96、某商场开展购物优惠活动:一次购买300元及以下的商品九折优惠;一次购买超过300元的商品,其中300元九折优惠,超过300元的部分八折优惠。小王购物第一次付款144元,第二次又付款310元。如果他―次购买并付款,可以节省多少元?_____
A: 16B: 22.4C: 30.6D: 48
参考答案: A 本题解释:A【解析】统筹优化问题。由题意,第一次付款144元可得商品原价为160元;第二次付款为310元,可得原价为350元。故总价510元,按照优惠,需付款300×0.9+210×0.8=438元,节省了454-438=16元。
97、某市对52种建筑防水卷材产品进行质量抽检,其中有8种产品的低温柔度不合格,10种产品的可溶物含量不达标,9种产品的接缝剪切性能不合格,同时两项不合格的有7种,有1种产品这三项都不合格,则三项全部合格的建筑防水卷材产品有多少种?_____
A: 37B: 36C: 35D: 34
参考答案: D 本题解释:正确答案是D考点容斥原理问题解析本题注意按照不合格得到三个类,进行容斥原理分析。分别设三项全部合格、仅一项不合格的产品有A、B种,根据题意可得B+7+1=52-A,3×1+2×7+1×B=8+10+9,解得A=34,B=10。故正确答案为D。公式:三集合容斥原理中,将只符合一个条件、只符合两个条件和三个条件都符合的分别看做三个整体,以A、B、C表示三个集合,以X、Y、Z分别表示只符合一个条件、只符合两个条件和三个条件都满足的部分,则有A+B+C=X+2Y+3Z及A∪B∪C=X+Y+Z成立。标签整体考虑公式应用
98、已知2008被一些自然数去除,得到的余数都是10,那么,这些自然数共有_____。
A: 10B: 11C: 12D: 9
参考答案: B 本题解释:【答案解析】解析:余10=>说明2008-10=1998都能被这些数整除。同时,1998=2×3×3×3×37,所以,取1个数有37,2,3。---3个。,只取2个数乘积有3×37,2×37,3×3,2×3。---4个。,只取3个数乘积有3×3×37,2×3×37,3×3×3,2×3×3。---4个。只取4个数乘积有3×3×3×37,2×3×3×37,2×3×3×3。---3个。只取5个数乘积有2×3×3×3×37---1个。总共3+4+4+3+1=15,但根据余数小于除数的原理,余数为10,因此所有能除2008且余10的数,都应大于10=>2,3,3×3,2×3被排除。综上,总共有3+4+4+3+1-4=11个。
99、一只猎豹锁定了距离自己200米远的一只羚羊,以108千米/小时的速度发起进攻,2秒钟后,羚羊意识到危险,以72千米/小时的速度快速逃命。问猎豹捕捉到羚羊时,羚羊跑了多少路程?_____
A: 520米 B: 360米 C: 280米 D: 240米
参考答案: C 本题解释:【答案】C。解析:108千米/小时=30米/秒,72千米/小时=20米/秒,开始猎豹距离羚羊200米,羚羊意识到危险的时候,猎豹距离羚羊200米-30米/秒×2秒=140米。根据追击问题计算公式:速度差×追击时间=路程差,即(30-20)t=140,t=14秒,即猎豹捕捉到羚羊时,羚羊跑了14秒,路程为20×14=280米。
100、一车行共有65辆小汽车,其中45辆有空调,30辆有高级音响,12辆兼而有之。既没有空调也没有高级音响的汽车有几辆?_____
A: 2;B: 8;C: 10;D: 15;
参考答案: A 本题解释:【答案解析】:选A,车行的小汽车总量=只有空调的+只有高级音响的+两样都有的+两样都没有的,只有空调的=有空调的-两样都有的=45-12=33,只有高级音响的=有高级音响的-两样都有的=30-12=18,令两样都没有的为x,则65=33+18+12+x=>x=2