微信搜索关注"91考试网"公众号,领30元,获取公务员、事业编、教师等考试资料40G!
1、校对一份书稿,编辑甲每天的工作效率等于编辑乙、丙每天工作效率之和,丙的工作效率相当于甲、乙每天工作效率之和的 。如果三人一起校对只需6天就可完成。现在如果让乙一人单独校对这份书稿,则需要_____天才能完成。
。如果三人一起校对只需6天就可完成。现在如果让乙一人单独校对这份书稿,则需要_____天才能完成。
A: 20B: 16C: 24D: 18
参考答案: D 本题解释:参考答案 题目详解:三人一起完成校对需要6天,那么三人每天的效率之和是:
题目详解:三人一起完成校对需要6天,那么三人每天的效率之和是: ,甲每天的工作效率等于乙、丙每天工作效率之和,那么甲的工作效率为:
,甲每天的工作效率等于乙、丙每天工作效率之和,那么甲的工作效率为: ,乙、丙的效率和是:
,乙、丙的效率和是: ;设乙单独完成校对需要x天,那么根据题意可得到方程:
;设乙单独完成校对需要x天,那么根据题意可得到方程: 解得
解得 ,即乙单独完成校对需要18天。所以,选D。考查点:数量关系>数学运算>工程问题>单独完工问题
,即乙单独完成校对需要18天。所以,选D。考查点:数量关系>数学运算>工程问题>单独完工问题
2、原计划用24个工人挖一定数量的土,按计划工作5天后,因为调走6人,于是剩下的工人每天比原计划多挖1方土才能如期完成任务,则原计划每人每天挖土_____。
A: 6方B: 5方C: 4方D: 3方
参考答案: D 本题解释:参考答案 题目详解:解法一:调走6人后,还剩下18人,每人每天增1方,则一天共增加18方,为这6个人的工作量,所以
题目详解:解法一:调走6人后,还剩下18人,每人每天增1方,则一天共增加18方,为这6个人的工作量,所以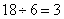 (方),因此,选D。解法二:设原计划每人每天挖土X方,调走人后每人每天挖土
(方),因此,选D。解法二:设原计划每人每天挖土X方,调走人后每人每天挖土 方,可列方程为:
方,可列方程为: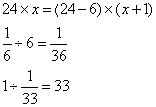
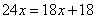
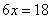
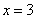 所以原计划每人每天挖土3方。因此,选D。考查点:数量关系>数学运算>工程问题>合作完工问题
所以原计划每人每天挖土3方。因此,选D。考查点:数量关系>数学运算>工程问题>合作完工问题
3、(2009河北选调,第60题)甲、乙两队合作收割一块稻田,7小时可以完成。两队共同收割5小时后,甲队所有队员及乙队人数的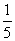 调做其他工作,又经过6小时,全部收割完,甲队单独收割这块稻田时需要多少小时?_____
调做其他工作,又经过6小时,全部收割完,甲队单独收割这块稻田时需要多少小时?_____
A: 10B: 12C: 15D: 20
参考答案: B 本题解释:参考答案:B题目详解:解法一:假设工程总量为“7”,由题意易知: 因此,甲队单独收割需要
因此,甲队单独收割需要 (小时)。解法二:由甲乙合作7小时完成,可以把总工作量看作7份。甲乙合作5小时后,还剩2份,这两份由乙的
(小时)。解法二:由甲乙合作7小时完成,可以把总工作量看作7份。甲乙合作5小时后,还剩2份,这两份由乙的 人数用6小时完成,则:乙的效率为:
人数用6小时完成,则:乙的效率为: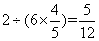 ,甲的效率为:
,甲的效率为: 。那么甲单独做需要时间为:
。那么甲单独做需要时间为: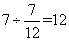 小时。因此,选B。考查点:数量关系>数学运算>工程问题>单独完工问题
小时。因此,选B。考查点:数量关系>数学运算>工程问题>单独完工问题
4、(2008广东,第6题)一项任务甲做要半小时完成,乙做要45分钟完成,两人合作需要多少分钟完成?_____
A: 12B: 15C: 18D: 20
参考答案: C 本题解释:参考答案:C题目详解:根据题意,设工作总量为“1”,则有:甲每分钟完成任务的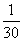 ,乙每分钟完成任务的
,乙每分钟完成任务的 ,合作完成时间为
,合作完成时间为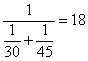 。因此,选C。考查点:数量关系>数学运算>工程问题>合作完工问题
。因此,选C。考查点:数量关系>数学运算>工程问题>合作完工问题
5、某工程由小张、小王两人合作刚好可在规定的时间内完成。如果小张的工作效率提高 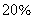 ,那么两人只需用规定时间的
,那么两人只需用规定时间的 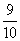 就可完成工程;如果小王的工作效率降低
就可完成工程;如果小王的工作效率降低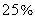 ,那么两人就需延迟2.5小时完成工程。规定的时间是_____。
,那么两人就需延迟2.5小时完成工程。规定的时间是_____。
A: 20小时B: 24小时C: 26小时D: 30小时
参考答案: A 本题解释:参考答案:A题目详解:设规定的时间是C。小张的工作效率是A,小王的工作效率为B,那么: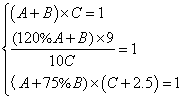 解得,
解得,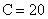 (小时)。所以,选A。考查点:数量关系>数学运算>工程问题>合作完工问题
(小时)。所以,选A。考查点:数量关系>数学运算>工程问题>合作完工问题
6、一项工程,甲、乙两人合作4天后,再由乙单独做5天完成,已知甲比乙每天多完成这项工程的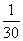 。甲、乙单独做这项工程各需要几天?_____
。甲、乙单独做这项工程各需要几天?_____
A: 15,30B: 10,15C: 20,60D: 12,20
参考答案: B 本题解释:参考答案:B题目详解:已知:甲比乙每天多完成这项工程的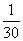 ,那么:甲4天比乙4天多完成
,那么:甲4天比乙4天多完成 。把这
。把这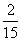 减去,那么甲4天和乙4天就做一样多了。也就是说甲4天+乙4天=乙8天,再加上乙5天,就是乙13天做了:
减去,那么甲4天和乙4天就做一样多了。也就是说甲4天+乙4天=乙8天,再加上乙5天,就是乙13天做了: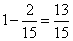 乙单独做需要:
乙单独做需要: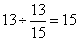 (天),甲单独做需要:
(天),甲单独做需要: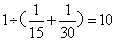 (天)。因此,选B。考查点:数量关系>数学运算>工程问题>合作完工问题
(天)。因此,选B。考查点:数量关系>数学运算>工程问题>合作完工问题
7、一件工程,甲单独完成需2天,乙单独完成需要4天,如果甲干完一天后,剩下的工程由乙单独完成,则干完此项工程共需_____。
A: 3天B: 4天C: 5天D: 6天
参考答案: A 本题解释:参考答案:A题目详解:解法一:设工作总量为“1”,那么:甲每天做的工作量为: ,乙每天做的工作量为:
,乙每天做的工作量为: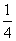 ,甲做1天后剩下的部分乙要做
,甲做1天后剩下的部分乙要做 天,则一共需
天,则一共需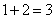 天。因此,选A。解法二:因为甲独干需两天,乙单独干需四天,现在甲干了乙干,则所需时间一定介于他俩单独干的天数之间,因此选A。(该解析由用户“你猜我是谁”于2011-03-0513:57:34贡献,感谢感谢!)考查点:数量关系>数学运算>工程问题>合作完工问题
天。因此,选A。解法二:因为甲独干需两天,乙单独干需四天,现在甲干了乙干,则所需时间一定介于他俩单独干的天数之间,因此选A。(该解析由用户“你猜我是谁”于2011-03-0513:57:34贡献,感谢感谢!)考查点:数量关系>数学运算>工程问题>合作完工问题
8、甲、乙、丙三个工程队的效率比为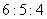 ,现将
,现将 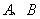 两项工作量相同的工程交给这三个工程队,甲队负责
两项工作量相同的工程交给这三个工程队,甲队负责 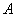 工程,乙队负责
工程,乙队负责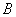 工程,丙队参与
工程,丙队参与 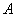 工程若干天后转而参与
工程若干天后转而参与 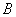 工程。两项工程同时开工,耗时16天同时结束,问丙队在
工程。两项工程同时开工,耗时16天同时结束,问丙队在 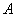 工程中参与施工多少天?_____
工程中参与施工多少天?_____
A: 6B: 7C: 8D: 9
参考答案: A 本题解释:参考答案:A题目详解:解法一:由题意可设甲、乙、丙每日工作量分别为6、5、4,丙队参与A工程x天,那么参加B工程(16-x)天,根据A、B工作量相同可列方程: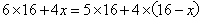 解得,
解得,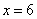 。所以,选A。解法二:采用代入排除法。由于甲效率比乙高,所以丙在甲的
。所以,选A。解法二:采用代入排除法。由于甲效率比乙高,所以丙在甲的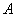 工程参与时间少,由此可排除C、D。代入A、B知,
工程参与时间少,由此可排除C、D。代入A、B知,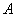 满足条件。所以选择A选项。考查点:数量关系>数学运算>工程问题>合作完工问题
满足条件。所以选择A选项。考查点:数量关系>数学运算>工程问题>合作完工问题
9、有甲、乙两根水管,分别同时给A、B两个大小相同的水池注水,在相同的时间里甲、乙两管注水量之比是 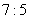 。经过
。经过 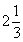 小时,A、B两池中注入的水之和恰好是一池。这时,甲管注水速度提高
小时,A、B两池中注入的水之和恰好是一池。这时,甲管注水速度提高 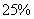 ,乙管的注水速度不变,那么,当甲管注满A池时,乙管再经过多少小时注满B池?_____
,乙管的注水速度不变,那么,当甲管注满A池时,乙管再经过多少小时注满B池?_____
A: 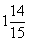 B:
B: 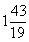 C: 1D:
C: 1D: 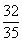
参考答案: A 本题解释:参考答案:A题目详解:根据题意,设水池容积为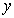 ,甲管每小时注水
,甲管每小时注水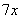 ,乙管每小时注水
,乙管每小时注水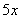 。则
。则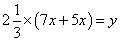 ,得到
,得到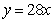 ;甲已经灌了
;甲已经灌了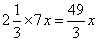 ,还剩下
,还剩下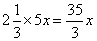 ,此时甲管注水速度提高
,此时甲管注水速度提高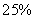 ,甲每小时注水速度为
,甲每小时注水速度为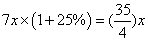 ,因此甲注满水池还需要:
,因此甲注满水池还需要: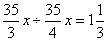 时;乙最开始灌了
时;乙最开始灌了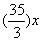 ,还剩
,还剩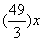 ,保持原速度的话当甲灌满水池时乙灌了
,保持原速度的话当甲灌满水池时乙灌了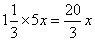 ,还差
,还差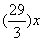 ,乙还需要
,乙还需要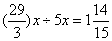 小时才可注满B池。因此,选A。考查点:数量关系>数学运算>工程问题>合作完工问题
小时才可注满B池。因此,选A。考查点:数量关系>数学运算>工程问题>合作完工问题
10、有两个工程队完成一项工程,甲队每工作6天后休息1天,单独做需要76天完工;乙队每工作5天后休息2天,单独做需要89天完工,照这样计算,两队合作,从1998年11月29日开始动工,到1999年几月几日才能完工?_____
A: 1月9日B: 1月10日C: 1月11日D: 1月8日
参考答案: D 本题解释:参考答案 题目详解:根据题意,可知:甲单独做了76天完工,因为
题目详解:根据题意,可知:甲单独做了76天完工,因为 ,则实际工作:
,则实际工作: 天,乙单独做了89天完工,因为
天,乙单独做了89天完工,因为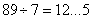 ,则实际工作:
,则实际工作: 天,则甲乙的工作效率分别为
天,则甲乙的工作效率分别为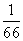 ,
, ;在一个7天周期内合作共完成
;在一个7天周期内合作共完成 ,
, ,也就是需要5个七天后还剩
,也就是需要5个七天后还剩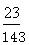 (此处七天工作量为1),也就是差
(此处七天工作量为1),也就是差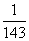 的量刚好一个七天的周期,而甲每天完成的量为
的量刚好一个七天的周期,而甲每天完成的量为 ,所以第六个七天工作了6天。所以共用了
,所以第六个七天工作了6天。所以共用了 ,所以,将在1999年1月8日完工。因此,选D考查点:数量关系>数学运算>工程问题>合作完工问题
,所以,将在1999年1月8日完工。因此,选D考查点:数量关系>数学运算>工程问题>合作完工问题
11、甲、乙合作完成一项工作,由于配合得好,甲的工作效率比单独做时提高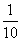 ,乙的工作效率比单独做时提高
,乙的工作效率比单独做时提高 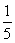 ,甲、乙合作6小时完成了这项工作,如果甲单独做需要11小时,那么乙单独做需要几小时?_____
,甲、乙合作6小时完成了这项工作,如果甲单独做需要11小时,那么乙单独做需要几小时?_____
A: 15B: 16C: 17D: 18
参考答案: D 本题解释:参考答案 题目详解:根据题意,可知:甲、乙合作的效率是:
题目详解:根据题意,可知:甲、乙合作的效率是: ;甲单独做的效率是:
;甲单独做的效率是: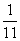 ,合作时甲效率提高
,合作时甲效率提高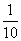 ,因此甲、乙合作时,甲的效率是:
,因此甲、乙合作时,甲的效率是: ,乙的效率:
,乙的效率: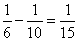 ;乙单独做的时候是合作时候的
;乙单独做的时候是合作时候的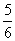 ,因此乙单独做效率是:
,因此乙单独做效率是: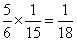 ;乙单独做需要的时间为:
;乙单独做需要的时间为: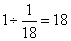 (小时)。所以,选D。考查点:数量关系>数学运算>工程问题>单独完工问题
(小时)。所以,选D。考查点:数量关系>数学运算>工程问题>单独完工问题
12、(2009吉林,第7题)甲、乙一起工作来完成一项工程,如果甲单独完成需要30天,乙单独完成需要24天,现在甲、乙一起合作来完成这项工程,但是乙中途被调走若干天,去做另一项任务,最后完成这项工程用了20天,问乙中途被调走_____天。
A: 8B: 3C: 10D: 12
参考答案: D 本题解释:参考答案 题目详解:解法一:假设工程总量为“120”(30与24的最小公倍数),由题意易知:甲的工作效率为:
题目详解:解法一:假设工程总量为“120”(30与24的最小公倍数),由题意易知:甲的工作效率为: ,乙的工作效率为:
,乙的工作效率为: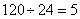 。甲和乙一起合作来完成时,甲全程20天都参加了,甲的工作量为:
。甲和乙一起合作来完成时,甲全程20天都参加了,甲的工作量为: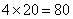 ,剩下
,剩下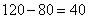 的工作量由乙来完成,乙完成剩下工作需要花:
的工作量由乙来完成,乙完成剩下工作需要花: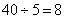 (天),因此乙中途被调走了:
(天),因此乙中途被调走了: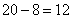 (天)。解法二:通过比例代换的口算来得到答案:甲单独完成需要30天,那么后来20天肯定是完成了工程的
(天)。解法二:通过比例代换的口算来得到答案:甲单独完成需要30天,那么后来20天肯定是完成了工程的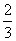 ,剩下
,剩下 是由乙完成的,乙完成全部需要24天,那么完成
是由乙完成的,乙完成全部需要24天,那么完成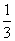 肯定需要8天。所以,乙中途被调走了:20-8=12(天)。因此,选D。考查点:数量关系>数学运算>工程问题>合作完工问题
肯定需要8天。所以,乙中途被调走了:20-8=12(天)。因此,选D。考查点:数量关系>数学运算>工程问题>合作完工问题
13、(2009山东,第119题)某工程项目由甲项目公司单独做需4天完成,由乙项目公司单独做需6天才能完成,甲、乙、丙三个公司共同做2天就可以完成,现因交工日期在即,需多公司合作,但甲公司因故退出,则由乙、丙公司合作完成共需多少天?_____
A: 3B: 4C: 5D: 6
参考答案: B 本题解释:参考答案:B题目详解:假设工程总量为“12”,由题意易知:甲的效率为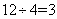 ,乙的效率为
,乙的效率为 ,甲、乙、丙的效率和为
,甲、乙、丙的效率和为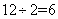 ,从而我们知道丙的效率为
,从而我们知道丙的效率为 。因此,乙、丙合作完成需要
。因此,乙、丙合作完成需要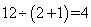 (天)。因此,选B。考查点:数量关系>数学运算>工程问题>合作完工问题
(天)。因此,选B。考查点:数量关系>数学运算>工程问题>合作完工问题
14、某工程甲单独做50天可以完成,乙单独做75天可以完成;现在两人合作,但途中乙因事离开了几天,最后一共花了40天把这项工程做完,则乙中途离开了_____天。
A: 15B: 16C: 22D: 25
参考答案: D 本题解释:参考答案 题目详解:根据题意,设整个工程总量为“1”,则有:乙中途离开,但是甲从始至终工作了40天,那么甲的工作量为:
题目详解:根据题意,设整个工程总量为“1”,则有:乙中途离开,但是甲从始至终工作了40天,那么甲的工作量为: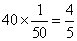 ;该工程中乙需要做的工作量为:
;该工程中乙需要做的工作量为: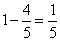 ;乙需要用了
;乙需要用了 天完成;故乙离开了
天完成;故乙离开了 天。所以,选D考查点:数量关系>数学运算>工程问题>合作完工问题
天。所以,选D考查点:数量关系>数学运算>工程问题>合作完工问题
15、有一批零件,甲、乙两种车床都可以加工。如果甲车床单独加工,可以比乙车床单独加工提前10天完成任务。现在用甲、乙两车床一起加工,结果12天就完成了任务。如果只用甲车床单独加工需多少天完成任务?_____
A: 20天B: 30C: 40D: 45
参考答案: A 本题解释:参考答案:A题目详解:设甲单独加工x天,乙单独加工 天完成,则甲的工作效率为:
天完成,则甲的工作效率为: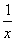 ,乙的工作效率为:
,乙的工作效率为: ;而甲乙合作的效率为:
;而甲乙合作的效率为: ,即:
,即: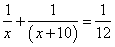 ,解得
,解得 。所以,选A。考查点:数量关系>数学运算>工程问题>单独完工问题
。所以,选A。考查点:数量关系>数学运算>工程问题>单独完工问题
16、甲、乙、丙三人在A、B两块地植树,A地要植900棵,B地要植1250棵。已知甲、乙、丙每天分别能植树24、30、32棵,甲在A地植树,丙在B地植树,乙先在A地植树,然后转到B地植树。两块地同时开始同时结束,乙应在开始后第几天从A地转到B地?_____
A: 8B: 10C: 12D: 11
参考答案: D 本题解释:参考答案 题目详解:甲、乙、丙三人一共需要种树:900+1250=2150棵,甲、乙、丙三人每天一共可以种树:
题目详解:甲、乙、丙三人一共需要种树:900+1250=2150棵,甲、乙、丙三人每天一共可以种树: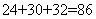 棵,如果种树2150棵,则三人共需种:2150÷86=25天,甲在A地种25天,能够种植600棵,还剩:
棵,如果种树2150棵,则三人共需种:2150÷86=25天,甲在A地种25天,能够种植600棵,还剩: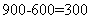 (棵),则需要乙在A地种植:
(棵),则需要乙在A地种植: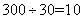 天,然后乙转到B地,丙、乙两人在B地种的棵数为
天,然后乙转到B地,丙、乙两人在B地种的棵数为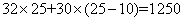 棵。所以答案是乙应该在A地种植10天,即应该从第11天开始从A地转移到B地。因此,选D。考查点:数量关系>数学运算>工程问题>合作完工问题
棵。所以答案是乙应该在A地种植10天,即应该从第11天开始从A地转移到B地。因此,选D。考查点:数量关系>数学运算>工程问题>合作完工问题
17、(2008陕西,第16题)一项工程,工作效率提高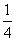 ,完成这项工程的时间将由原来的10小时缩短到几小时?_____
,完成这项工程的时间将由原来的10小时缩短到几小时?_____
A: 4B: 8C: 12D: 16
参考答案: B 本题解释:参考答案:B题目详解:假设原来工作效率为4,工作总量应该为: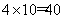 ,工作效率提高
,工作效率提高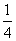 后变为:
后变为: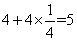 ,时间缩短到:
,时间缩短到: (小时)。所以,选B。考查点:数量关系>数学运算>工程问题>单独完工问题
(小时)。所以,选B。考查点:数量关系>数学运算>工程问题>单独完工问题
18、师徒两人合作完成一项工程,由于配合得好,师傅的工作效率比单独做时要提高 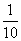 ,徒弟的工作效率比单独做时提高
,徒弟的工作效率比单独做时提高 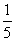 。两人合作6天,完成全部工程的
。两人合作6天,完成全部工程的 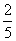 ,接着徒弟又单独做6天,这时这项工程还有
,接着徒弟又单独做6天,这时这项工程还有  未完成,如果这项工程由师傅一人做,几天完成?_____
未完成,如果这项工程由师傅一人做,几天完成?_____
A: 30B: 33C: 36D: 42
参考答案: B 本题解释:参考答案:B题目详解:根据题意,可知:两人合作6天完成 ,每天完成
,每天完成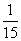 ,徒弟单独做了
,徒弟单独做了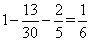 ,则徒弟单独做时每天完成:
,则徒弟单独做时每天完成: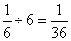 。已知徒弟合作时工作效率比单独做高
。已知徒弟合作时工作效率比单独做高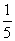 ,那么徒弟合作时每天完成:
,那么徒弟合作时每天完成: 。师傅合作时的效率是每天做:
。师傅合作时的效率是每天做: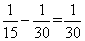 ,那么师傅单独做的效率为:
,那么师傅单独做的效率为: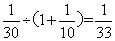 。所以,这项工作由师傅一人做,需要:
。所以,这项工作由师傅一人做,需要: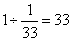 (天)。所以,选B考查点:数量关系>数学运算>工程问题>合作完工问题
(天)。所以,选B考查点:数量关系>数学运算>工程问题>合作完工问题
19、(2006江西)运送一批货物总运费为4200元,A、B两家运输公司同时运送8小时完成,A公司单独运输需14小时完成。现由A公司单独运送若干小时后,再由B公司单独运送剩下的货物。这样共用18小时全部运完。那么A、B两公司应分别获得:_____
A: 2100元,2100元B: 600元,3600元C: 1400元,2800元D: 800元,3400元
参考答案: B 本题解释:参考答案:B题目详解:解法一根据题意,设A、B两家运输公司的工作效率分别为x,y第一种运送方式的工作总量为:工作总量=工作效率×工作时间=8(x+y);第二种运送方式的工作总量为:工作总量=工作效率×工作时间=14x;由一二两种运送方式,得出8(x+y)=14x,解得x:y=4:3;第三种运送方式工作总量为:设现甲单独运送了t小时,则乙继续运送时间为(18-t),工作总量=甲的工作总量+乙的工作总量=甲的工作效率×甲的工作时间+乙的工作效率×乙的工作时间=xt+y(18-t),因为工作总量是一定的,所以xt+y(18-t)=14x,解得t=2;得出运输费用为:工作效率×工作时间×总费用,所以A运输公司所得费用:4200×1/14×2=600元;B公司的费用:4200-600=3600;因此,选B。解法二根据题意,设总工作量为"1”A公司的工作效率:工作效率=工作总量÷工作时间=1÷14=1/14;A、B公司的工作效率之和:工作效率=工作总量÷工作时间=1÷8=1/8;故B公司工作效率为:A、B公司工作效率之和-A工作效率=1/8-1/14=3/56;设A运送了t小时,则第三种运送方式的工作总量为:工作总量=工作效率×工作时间=1/14t+3/56(18-t)=1;解得t=2。得出运输费用为:工作效率×工作时间×总费用,所以A运输公司所得费用:4200×1/14×2=600元;B公司的费用:4200-600=3600;因此,选B。考查点:数量关系>数学运算>工程问题>合作完工问题
20、(2009黑龙江)某项工作,甲单独做要18小时完成,乙要24小时完成,丙要30小时才能完成。现按甲、乙、丙的顺序轮班做,每人工作一小时后换班。问当该项工作完成时,乙共做了多长时间?_____
A: 7小时44分B: 7小时58分C: 8小时D: 9小时10分
参考答案: A 本题解释:参考答案:A题目详解:解法一:根据题意,设工作总量为1,则:甲每小时完成: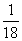 ,乙每小时完成:
,乙每小时完成: ,丙每小时完成:
,丙每小时完成: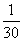 ,所以三个人各工作一小时可完成:
,所以三个人各工作一小时可完成: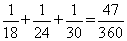 。
。 ,所以三人各工作7小时后,还剩下
,所以三人各工作7小时后,还剩下 没有完成,由于
没有完成,由于 ,所以乙工作的时间为:
,所以乙工作的时间为: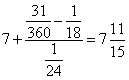 小时,即为7小时44分钟。因此,选A。解法二:18、24、30的最小公倍数是360,根据题意,有:甲、乙、丙三人各工作一小时可完成:
小时,即为7小时44分钟。因此,选A。解法二:18、24、30的最小公倍数是360,根据题意,有:甲、乙、丙三人各工作一小时可完成: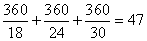
 甲再工作一小时还剩:
甲再工作一小时还剩: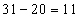
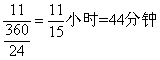 所以乙的工作时间为:7小时44分钟考查点:数量关系>数学运算>工程问题>合作完工问题
所以乙的工作时间为:7小时44分钟考查点:数量关系>数学运算>工程问题>合作完工问题