1、甲、乙两时钟都不正确，甲钟每走24小时，恰好快1分钟;乙钟每走24小时，恰好慢1分钟。假定今天下午三点钟的时候，将甲、乙两钟都调好，指在准确的时间上，任其不停地走下去，问下一次这两只钟都同样指在三点时，要隔多少天?_____
A: 30B: 240C: 480D: 720
参考答案: D 本题解释:【答案解析】可以先求出甲钟比标准时钟多转一圈所需天数，标准时钟比乙钟多走一圈所需天数，然后再求二者的最小公倍数。甲钟与标准时钟下一次同时指向三点时，甲钟比标准时钟多转一圈，也就是多走12小时，即60×12分钟，需要60×12÷(61-60)=720÷1=720(天)同样，标准时钟与乙钟下一次同时指向三点时，标准时钟比乙钟多转一圈，需要60×12÷(60-59)=720÷1=720(天)所以，经过720天后，甲、乙两钟同时指在三点。故正确答案为D。

2、有两个山村之间的公路都是上坡和下坡，没有平坦路。客车上坡的速度保持20千米/小时，下坡的速度保持30千米/小时。现知客车在两个山村之间往返一次，需要行驶4小时。请问这两个山村之间的距离有多少千米?_____
A: 45B: 48C: 50D: 24
参考答案: B 本题解释: 【解析】B。根据平均速度公式可知，全程的平均速度是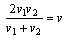：，全程的平均速度是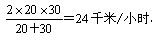：。（已知往返速度，求全程的平均速度，是有简便的算法的，要熟练把握。）两山村之间的路程是：（24×4）2=48千米。

3、某服装店老板去采购一批商品，其所带的钱如果只买某种进口上衣可买120件，如果只买某种普通上衣则可买180件。现在知道，最后该老板买的进口上衣和普通上衣的数量相同，问他最多可以各买多少件?_____
A: 70B: 72C: 74D: 75
参考答案: B 本题解释:

4、一百张牌抽掉奇数牌，然后再抽掉剩下牌中位于奇数位的牌……如此最后剩下的一张是原来100张牌排序中的第几张呢？_____
A: 63 B: 64 C: 65 D: 66
参考答案: B 本题解释:B

5、某工厂有学徒工、熟练工、技师共80名，每天完成480件产品的任务。已知每天学徒工完成2件，熟练工完成6件，技师完成7件，且学徒工和熟练工完成的量相等，则该厂技师人数是熟练工人数的_____倍。
A: 6B: 8C: 10D: 12
参考答案: D 本题解释:列方程组。设学徒工、熟练工、技师分别有x，y，z名。则有：X+Y+Z=80，2X-96Y+7Z=48012X=6Y得到：X=15，y=5，Z=60，所以Z：Y=60：5=12。选D。

6、一个20人的班级举行百分制测验，平均分为79分，所有人得分都是整数且任意两人得分不同。班级前5名的平均分正好是16到20名平均分的2倍。则班级第6名和第15名之间的分差最大为多少分？_____
A: 34B: 37C: 40D: 43
参考答案: D 本题解释:【答案】D。解析：求班级第6名和第15名之间的分差最大，则第6名的成绩要尽可能的接近第5名的成绩，且前5名的成绩差距要尽可能的小，即前6名成绩是连续的自然数，第15名的成绩要尽可能的接近第16名的成绩，且后5名的成绩差距要尽可能的小，即后6名的成绩是连续的自然数。又由于班级前5名的平均分正好是16到20名平均分的2倍，则前5名的成绩决定了后5名的成绩。而同时满足这些条件的数列有多组，则可以使前5名的成绩为100、99、98、97、96，则第6名的成绩为95，由此，后5名得成绩为51、50、49、48、47，则第15名得成绩为52，所以第6名和第15名之间的分差最大为95-52=43。因此，本题答案选择D选项。

7、小张每连续工作5天后休息3天，小周每连续工作7天后休息5天。假如3月1日两人都休息，3月2日两人都上班，问三月份有多少天两人都得上班？_____
A: 12B: 14C: 16D: 18
参考答案: B 本题解释:【答案】B。解析：解析1：前者8天一个循环周期，后者12天一个循环周期，两者最小公倍数为24。在三月份中从3月2日到3月25日，两人重合的工作天数为9天。在3月26日至3月31日的6天中，前5天两人同时工作。因此共计14天。故正确答案为B。解析2：用图表示如下，其中×表示工作，○表示休息，下图从3月2日起：小张：×××××○○○×××××○○○×××××○○○×××××○小周：×××××××○○○○○×××××××○○○○○××××××由图可知有14天两人都得上班。故正确答案为B。

8、有四个数，其中每三个数的和分别是45，46，49，52，那么这四个数中最小的一个数是多少_____
A: 12B: 18C: 36D: 45
参考答案: A 本题解释:【答案】A。解析：把四个数加起来，正好相当于把每个人算了3次，因此四人的作品那个岁数为(45+46+49+52)÷3=64，那么年龄最小的为64-52=12岁。

9、林文前年买了8000元的国家建设债券，定期3年。到期他取回本金和利息一共10284.8元。这种建设债券的年利率是多少?_____
A: 9.52%B: 9.6%C: 8.4%D: 9.25%
参考答案: A 本题解释:A。【解析】求利息的公式：利息=本金×利率×时间，可得出：利率=利息÷时间÷本金。而他3年所得的利息是：10284.8-8000=2284.8（元）;这样即可求出这债券的年利率是多少。（10284.8-8000）÷3÷8000=2284.8÷3÷8000=761.6÷8000=0.0952=9.52%。

10、教室里有若干学生，走了10名女生后，男生是女生人数的2倍，又走了9名男生后，女生是男生人数的5倍。问：最初有多少名女生?_____
A: 15B: 12C: 10D: 9
参考答案: A 本题解释:A【解析】设最初有x名女生，则男生的数量为2(x-10)，由题意可列等式x-10=5[2(x-10)-9]，可得x=15。故选A。

11、某公司计划采购一批电脑，正好赶上促销期，电脑打9折出售，同样的预算可以比平时多买10台电脑。问该公司的预算在平时能多买多少台电脑?_____
A: 60.B: 70C: 80D: 90
参考答案: D 本题解释:【答案】D。解析：设平时可以购买x台，电脑打折前价格为100，则打折后为90，依题意100x=90（x+10），解得=90。

12、电影票10元一张，降价后观众增加一倍，收入增加1/5，则一张票降价多少元?_____
A: 8B: 6C: 4D: 2
参考答案: C 本题解释:【答案】C。设原来观众为1，设降价后为X元，则有(10×1)：2X=5：6，得出X=6，则降价4元，选C。

13、3种动物赛跑，已知狐狸的速度是兔子的 ，兔子的速度是松鼠的2倍，一分钟松鼠比狐狸少跑14米，那么半分钟兔子比狐狸多跑_____米。
A: 28B: 19C: 14D: 7
参考答案: C 本题解释:C【解析】由题意可得：兔子速度∶松鼠速度∶狐狸速度=6∶3∶4，又因为“一分钟松鼠比狐狸少跑14米”即半分钟松鼠比狐狸少跑7米，所以令半分钟兔子、松鼠、狐狸分别跑6a、3a、4a，4a-3a=7，故a=7，所以半分钟兔子比狐狸多跑6×7-4×7=14（米）。

14、某家店准备打折出售一批滞销的电脑，经核算，如果按正价打九折销售，每台还可盈利305元，如果打八折，就要亏损175元。那么这种电脑的进货价是_____元。
A: 4800B: 4625C: 4015D: 3940
参考答案: C 本题解释:这种电脑打九折和打八折的差价是305+175=480（元），那么正价为480÷（90%-80%）=4800（元），进货价为4800×90%-305=4015（元）。故本题答案为C。

15、商场销售某种商品的加价幅度为其进货价的40%，现商场决定将加价幅度降低一半来促销，商品售价比以前降低了54元。问该商品原来的售价是多少元？_____
A: 324B: 270C: 135D: 378
参考答案: D 本题解释:假设进价是10份，则原来售价是14份，现在售价是12份。差2份是54元，那么14份是54×7=378（元）。

16、篮球规则中得分有3分，2分，1分，若在一次比赛中，队员A一人得了13分，那么他的得分组合共_____种。
A: 18　B: 19　C: 20　D: 21
参考答案: D 本题解释:D[解析]当A的3分分别拿到4，3，2，1，0次的时候，对应的组合数分别是1，3，4，6，7，所以A的得分组合共有1+3+4+6+7=21种，选D。

17、一个正方体木块放在桌子上，每一面都有一个数，位于相对面两个数的和都等于13，小张能看到顶面和两个侧面，看到的三个数和为18；小李能看到顶面和另外两个侧面，看到的三个数的和为24，那么贴着桌子的这一面的数是多少？_____
A: 4B: 5C: 6D: 7
参考答案: B 本题解释:B。题目给出相对面数字之和为13的条件，则注意将其余条件中出现的相对面合在一起。从这一点出发，可以看出若将小张与小王看到的面合在一起，则实际共看到2个顶面与4个不同的侧面。而四个不同侧面恰为两组对面，也即其数字之和为13×2=26，因此顶面的数字为（18+24—26）÷2=8，于是底面数字为13—8=5。故选B。

18、一间长250米、宽10米、高4米的仓库放置了1000个棱长为1米的正方体箱子，剩余的空间为_____立方米。 B: 1500C: 5000D: 9000
参考答案: D 本题解释:【答案】D。解析：仓库的容量为250×10×4＝10000立方米，1000个棱长为1米的正方体箱子体积为1000×1×1×1＝1000立方米，则剩余空间为10000－1000＝9000平方米，故正确答案为D。

19、某地劳动部门租用甲、乙两个教室开展农村实用人才培训。两教室均有5排座位，甲教室每排可坐10人，乙教室每排可坐9人。两教室当月共举办该培训27次，每次培训均座无虚席，当月培训1290人次。问甲教室当月共举办了多少次这项培训? _____
A: 8B: 10C: 12D: 15
参考答案: D 本题解释:【解析】D。本题可直接看出答案，乙教室一次45人，共有1290人，所以乙次数一定为偶数，又因为一共27次，所以甲一定为奇数，直接选15。

20、现有红、黄、蓝三种颜色的珠子各若干颗，分给某班的52个学生，每个学生可以取1至3颗珠子，一种颜色的珠子最多只能取1颗。那么，这班学生中至少有_____人取的珠子完全相同。
A: 5B: 8C: 13D: 17
参考答案: B 本题解释:B[解析]取珠子的种类有如下7种：①红;②黄;③蓝;④红与黄;⑤红与蓝;⑥黄与蓝;⑦红、黄、蓝。从最不巧的情况想。每七个学生取的珠子的种类各不相同，因为52÷7(余3)，所以，至少有7+1(即8)个人取的珠子完全相同。故本题正确答案为B。

21、一群人坐车旅游，每辆车坐22人，剩5人没有座位，每辆坐26人，空出5个座位， 问每辆车坐25人，空出多少座位? _____
A: 20B: 15C: 10D: 5
参考答案: C 本题解释: C。一盈一亏型，车的数量为（15+5）÷ （26-22）=5,则共有5×22+5=115人。则坐25人时，115 ÷ 25=4……15，即需要5辆车，空出25-15=10个座位。

22、四年级学生搬砖，有12人每人各搬7块，有20人每人各搬6块，其余的每人搬5块，这样最后余下148块;如果有30人每人各搬8块，有8人每人搬9块，其余的每人搬10块，这样分配最后余下20块。学生共有多少人?_____
A: 80B: 76C: 48D: 24
参考答案: C 本题解释:C【解析】每人如果都搬5块，则共余下的块数：（7-5）×12+（6-5）×20+148=192（块）;把另一种分配方法改为，每人都搬10块，则砖总数不足：（10-8）×30+（10-9）×8-20=48（块）。设学生人数为x，则：5x+192=10x-48，故x=48（人）。

23、某公司招聘甲、乙两种职位的人员共90人，甲、乙两种职位人员每月的工资分别为1500元和2500元，若甲职位的工资总支出是乙职位的40%，则乙职位招聘人数比甲职位多：_____
A: 24人B: 20人C: 18人D: 15人
参考答案: C 本题解释:【答案】C。解析：设甲职位有x人，则Z乙职位有（90-x）人。依题意有l500x=2500×（90-x）×40%，x=36人。因此乙职位有90-36=54人，比甲职位多54-36=18人。快速突破甲、乙职位的人均工资之比为1500：2500=3：5;甲职位的工资总支出是乙职位的40%，则甲、乙职位的总工资支出之比为40%：1=2：5，所以甲、乙职位的招聘人位之比为2/3：5/5=2：3，甲、乙共招聘90人，则乙职位招聘人数比甲职位多90×（3-2）/（3+2）=18人。

24、在距离10千米的两城之间架设电线杆，若每隔50米立一个电线杆，则需要有_____个电线杆。
A: 15B: 201C: 100D: 250
参考答案: B 本题解释:B 【解析】所需数量为长度数除以间隔数加1。

25、一个商家要将自己的广告牌装在一条马路的一边，计划每隔4米装一块广告牌。在该马路上，每隔7米都栽种一棵树。已知这段马路长1092米，且一端是树，请问在不砍掉树的情况下，这段马路上可以装_____块广告牌。
A: 234B: 233C: 157D: 156
参考答案: A 本题解释:【答案】A。解析：方法一：如果没有树的话，马路应该可以装1092÷4+1=274（块）广告牌。但因为马路上原来栽有树木，则每隔4×7=28（米）处是树和广告牌重合的地方，不能立广告牌，只需求得广告牌与树木重合之处共有多少，减去即可。至此，本题转化成求在1092米的道路上，间隔28米，可栽种多少树木的问题。套入公式，该条道路上间隔28米处可以种树的棵数1092÷28+1=40。因此，这段马路上能装的广告牌的数量为：274—40=234（块）。方法二：题目可以看做是周期问题。每隔28米可装广告牌数量为28÷4+1=8（块），其中两端都种有树，则28米内可以装广告牌8—2=6（块）。1092米内间隔为28米的路段共有1092÷28=39（个），所以共可装广告牌的数量为6×39=234（块）。

26、Ａ大学的小李和B大学的小孙分别从自己学校同时出发，不断往返于A、B两校之间。现已知小李的速度为85米/分，小孙的速度为105米/分，且经过12分钟后两人第二次相遇。问A,B两校相距多少米?_____
A: 1140米B: 980米C: 840米D: 760米
参考答案: D 本题解释:易知到第二次相遇时，两人合起来走过的距离恰为A、B两校距离的3倍，因此A、B两校相距（85+105）×12÷3=760（米）。故选D。

27、有甲、乙两只钟表，甲表8时15分时，乙表8时31分。甲表比标准时间每9小时快3分，乙表比标准时间每7小时慢5分。至少要经过几小时，两钟表的指针指在同一时刻?_____
A: 12(7/11)B: 15C: 15(3/11)D: 17(8/11)
参考答案: C 本题解释: C 解析： 甲表比标准时间每小时快3/9=1/3分，乙表比标准时间每小时慢5/7分。甲、乙两表每小时相差是1/3+5/7=22/21分8时31分-8时15分=16分按追及问题，追及路程为16分，速度差是每小时22/21分，求追及时间。16÷22/21=16×21/22=15（3/11）（小时）至少再经过15311小时，两钟表的指针指在同一时刻。

28、某单位有60名运动员参加运动会开幕式，他们着装白色或黑色上衣，黑色或蓝色裤子。其中有12人穿白上衣蓝裤子，有34人穿黑裤子，29人穿黑上衣，那么穿黑上衣黑裤子的有多少人? _____
A: 12B: 14C: 15D: 19
参考答案: C 本题解释:C。【解析】有34人穿黑裤子，则有60-34=26个人穿蓝色裤子，26-12=14个人穿黑衣蓝裤，则有29-14=15个人穿黑衣黑裤

29、一项工程由甲单独做需要15天做完，乙单独做需要12天做完，二人合做4天后，剩下的工程由甲单独做，还需做几天方可做完？_____。
A: 6 B: 8C: 9 D: 5
参考答案: A 本题解释:A 【解析】依题意，甲每天完成总工程的1／15，乙每天完成总工程的1／12，甲、乙合作4天共完成（1／12+1／15） ×4=3／5，故剩下的工程甲需要的时间为（1—3／5）／（1／15）=6，总计算式即为[1一（1／12+1／15）]×4／（1／15）=6（天）。

30、某公司的6名员工一起去用餐，他们各自购买了三种不同食品中的一种，且每人只购买了一份。已知盖饭15元一份，水饺7元一份，面条9元一份，他们一共花费了60元。问他们中最多有几人买了水饺？_____
A: 1B: 2C: 3D: 4
参考答案: C 本题解释:【答案】C。解析：假定购买三种食物人数分别为X、Y、Z，根据题意X＋Y＋Z＝6，15X＋7Y＋9Z＝60。要使得水饺最多，则其他尽可能少。根据奇偶性质，可知X、Y、Z三个数中必然两个为奇数一个为偶数，或者三个均为偶数。将选项代入验证，若Y＝4，此时X、Z无正整数解；若Y＝3，可知X＝2，Z＝1，符合题意。因此正确答案为C。老师点睛:得到15X＋7Y＋9Z＝60后，注意到15、9、60均能被3整除，因此7Y必然能被3整除，仅C符合。

31、423×187-423×24-423×63的值是_____。
A: 41877B: 42300C: 42323D: 42703
参考答案: B 本题解释: B 【解析】原式可化为423×（187-24-63）。

32、有一个93人的参观团，其中男47人，女46人。他们住进一个旅馆内，旅馆内有可住11人、7人、4人的3种房间。要求男、女分住不同房间，且每个房间均住满，至少需要多少房间?_____
A: 11B: 10C: 13D: 17
参考答案: A 本题解释: A 解析： 设男的安排11人房间a间，7人房间b间，4人房间c间。则应满足等式11a+7b+4c=47。在这个等式中，a取尽量大的值a=3，b取最大值2，c取0。因此男的至少安排房间数为3+2+0=5（间）;设女的安排11人房间d间，7人房间e间，4人房间f间，则有11d+7e+4f=46。经试验不难看出，d=1，e=5，f=0。因此女的至少安排房间数为1+5+0=6（间）。总共至少安排房间：5+6=11（间）。故本题选A。

33、将10克盐和200克浓度为5%的盐水一起加入一杯水中，可得浓度为2.5%的盐水，则原来杯中水的克数是_____。
A: 570B: 580C: 590D: 600
参考答案: C 本题解释:C。

34、某个月有五个星期六，已知这五个日期的和为85，则这个月中最后一个星期六是多少号？_____
A: 10B: 17C: 24D: 31
参考答案: D 本题解释:【答案】D。解析：一个月有五个星期六，日期和为85，则平均数为17，因为五个星期六的日期构成公差为7的等差数列，平均数即是第三个星期六的日期，则第五个星期六的日期为17+7+7=31，故正确答案为D。

35、某人将一套房屋以购入价的3倍在房产中介处放盘。他告诉中介，一周内签约的买家其成交价能比放盘价再便宜5万元，并愿意支付成交价3%的中介费基础上，再多支付1万元给中介。若该房屋在一周内以100万元的价格成交，那么，此人在这套房屋上盈利_____万
A: 66B: 65C: 61D: 58
参考答案: C 本题解释:【答案】C。解析：成交价100，则据题意放盘价是100+5=105，可知购入价是105÷3=35，中介费是100X3%+1=3+1=4.可知盈利100-35-4=61。因此，本题答案选择C项。

36、将一根绳子连续对折三次，然后每隔一定长度剪一刀，共剪6刀。问这样操作后，原来的绳子被剪成几段？_____
A: 18段B: 49段C: 42段D: 52段
参考答案: B 本题解释:【答案】B。解析：对折三次，则绳子变成8折，在上面剪6刀，第一刀为8*1+1=9段；第二刀为8*2+1=17段，依次类推第六刀为8*6+1=49段，因此绳子被剪成49段。因此正确答案为B。

37、假定一对刚出生的小兔一个月能长成大兔，再过一个月便能生下一对小兔，并且此后每个月都生一对小兔。如果一切正常没有死亡，公母兔也比例适调，那么一对刚出生的兔子，一年可以繁殖成_____对兔子。
A: 144B: 233C: 288D: 466
参考答案: A 本题解释:【答案】A。解析：先列举出经过一到六个月兔子的对数分别是1、1、2、3、5、8。很容易发现这个数列的特点：即从第三项起，每一项都等于前两项之和。按这个规律写下去，便可得出一年内兔子繁殖的对数：1、1、2、3、5、8、13、21、34、55、89、144。可见一年内兔子共有144对。故正确答案为A。

38、某机关共有干部、职工350人，其中55岁以上共有70人。现拟进行机构改革，总体规模压缩为180人，并规定55岁以上的人裁减比例为70％。请问55岁以下的人裁减比例约是多少?_____。
A: 51％ B: 43％ C: 40％ D: 34%
参考答案: B

39、某天体沿正圆形轨道绕地球一圈所需时间为29.53059天，转速约1公里／秒。假设该天体离地球的距离比现在远10万公里而转速不变，那么该天体绕地球一圈约需要多少天？_____
A: 31 B: 32 C: 34 D: 37
参考答案: D 本题解释: D。算式为[29.53059×24×60×60×1/π+100000×2]×π÷1÷60÷60÷24≈36.8天，所以答案为D项。

40、一间长250米、宽10米、高4米的仓库放置了1000个棱长为1米的正方体箱子，剩余的空间是多少立方米?_____ B: 1500C: 5000D: 9000
参考答案: D 本题解释:D。【解析】进行简单的数字计算即可，250×10×4-1000×1=9000(m3)。

41、一项工程，甲单独做，6天可完成；甲乙合做，2天可完成；则乙单独做，_____天可完成。
A: 1.5 B: 3 C: 4 D: 5
参考答案: B 本题解释: B。设这项工程为单位1，则甲的速度为吉，甲乙共同速度为1/2么乙的速度为1/2-1/6-1/3则乙做完这项工程需要3天。故正确答案为B。

42、某商品76件，出售给33位顾客，每位顾客最多买3件。买1件按原定价，买2件降价10%，买3件降价20%。最后结算，平均每件恰好按原价的85%出售，那么买3件的顾客有多少人?_____
A: 14B: 10C: 7D: 2
参考答案: A 本题解释:A【解析】 买2件商品按原价的90%，买3件商品按原价的80%。由于 =85%，即1个人买1件与1个人买3件的平均，每件正好是原定价的85%;又由于 =85%，所以2个人买3件与3个人买2件的平均，每件正好是原价的85%。因此，买3件的人数是买1件的人数与买2件人数的之和。设买2件的有x人，则买1件的有（33-x- x）÷2（人），买3件的有 x+（33-x- x）÷2（人）。因为共有商品76件，于是有方程（33-x- x）÷2+2x+3×[ x+（33-x- x）÷2]=76，解出x=15（人）。买3件的有x+（33-x- x）÷=14（人）故买3件的顾客有14人。选A。

43、小王工作一年酬金是1800元和一台全自动洗衣机。他干了7个月，得到560元和一台洗衣机，问这台洗衣机价钱为多少元_____
A: 1176B: 1144C: 1200D: 1154
参考答案: A 本题解释:A[解析]小王工作5个月的酬金为1800—560=1240元，因此他工作一年的酬金相当于1240÷5×12=2976元，故洗衣机相当于2976-1800=1176元。

44、A、B两地相距1350米，甲和乙分别从A、B两地出发，相向而行。已知甲的速度为4千米/小时，乙的速度为5千米/小时，1分钟后两人调头反方向而行，再过3分钟，两人再次调头反方向而行，以此类推，再过5、7、……(连续奇数)分钟调头而行，请问，出发多少分钟后两人才能相遇?_____
A: 9B: 25C: 49D: 81
参考答案: D 本题解释:【答案解析】如果两人不调头走，两人相遇需要1350÷1000÷(4+5)×60=9分钟。如果以初始方向为正方向，则两个人分别走了1、-3、5、-7、……分钟的路程，由于9=1-3+5-7+9-11+13-15+17，则出发后1+3+5+7+9+11+13+15+17=81分钟两人相遇。

45、有一个长方体容器，长40厘米，宽30厘米，高10厘米，里面的水深6厘米(最大面为底面)。如果把这个容器盖紧，再竖起来(最小面为底面)，则里面的水深是多少厘米_____
A: 15厘米 B: 18厘米 C: 24厘米 D: 30厘米
参考答案: C 本题解释:【解析】C。盖紧后竖起前水的底面积为40×30平方厘米，深为6厘米，则体积为40×30×6立方厘米。盖紧后竖起水的体积不变，底面积变成了30×10平方厘米，此时水深应为。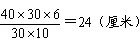

46、某单位《普法知识问答》的总平均分为87分，男同志的平均分为85分，女同志的平均分为90分，问此单位的男、女比例是多少？_____
A: 2/3B: 3/4 C: 3/2 D: 4/3
参考答案: C 本题解释:C。设女同志为1，男同志为 ，则（85x+90）÷（1+x）=87，解得x=3/2，即为男、女的比例，选C。

47、四个学生做加法练习，任写一个六位数，然后把个位数字(不等于0)移到这个数的最左边产生一个新的六位数，最后把这个新六位数与原数相加，分别得到以下四个六位数。则哪个结果有可能正确? _____
A: 172536B: 568741C: 620708D: 845267
参考答案: C 本题解释:

48、100人列队报数，报单数的离队，留下的再依次报数，报单数的再离队，这样重复多次，直到最后只留下一个人，请问此人在第一次报数时是第几号?_____
A: 32B: 50C: 64D: 100
参考答案: C 本题解释:C。第一次报数后，留下队员的号数是：2，4，6，8…96，98，100，均为的倍数;第二次报数后，留下队员的号数是：4，8，12…96，100，均为的倍数;第五次报数之后，留下队员的号数是的倍数;第六次报数之后，留下队员的号数四的倍数可见最后余下的一人在第一次报数时是第64号。

49、1-2+3-4+5-6+7-8+…+1989-1990+1991=_____
A: 895 B: 896 C: 995 D: 996
参考答案: D 本题解释: D。原式可等于1+1990/2=996。故正确答案为D。

50、电视台要播放一部30集电视连续剧，如果要求每天安排播出的集数互不相等，该电视剧最多可以播_____。
A: 7天B: 8天C: 9天D: 10天
参考答案: A 本题解释:[解析]正确答案为A。应尽可能减少每天播出的电视剧，才能增加播出天数，即第一天播1集，第二天播2集，以此类推，播到第六天时，共播了21集，第七天需播9集，如果拖到第八天，则一定会出现两天播出的电视剧集数量相同的情况，所以只能选A。

51、有11个人围成一个圆圈，依次编成1—11号，从1号起轮流表演节目，轮流的方法是：隔一个人表演一个节目，隔两个人表演一个节目，再隔一个人表演一个节目，隔两个人表演一个节目……这样轮流下去，至少要表演多少个节目，才能使每个人表演的次数同样?_____
A: 22B: 24C: 25D: 28
参考答案: A 本题解释:A【解析】本题考查的是周期问题。表演的人数共11人，且每个人表演次数相同，则至少要表演11N个节目。符合条件的只有A。

52、出租车队去机场接某会议的参会者，如果每车坐3名参会者，则需另外安排一辆大巴送走余下的50人；如每车坐4名参会者，则最后正好多出3辆空车。问该车队有多少辆出租车？_____
A: 50 B: 55 C: 60 D: 62
参考答案: D 本题解释:【解析】D.方程问题。设有x辆出租车，由题意列方程：3x+50=4（x-3），解得x=62.

53、某大型项目考察团队的所有员工年龄都在26～35岁之间，问：改考察团队至少有多少人才能保证在同一年出生的有5人？_____
A: 41B: 49C: 50D: 51
参考答案: A 本题解释:【答案】A。解析：最不利情况就是每年出生的人都有4个人，做题方法：最不利的情况数+1=4×10+1=41

54、一批树苗有100多棵，小王每天种8棵，第21天种完，小李每天种9棵，第18天种完。小孙每天种10棵，问第几天可以种完？_____
A: 14B: 15C: 17D: 18
参考答案: C 本题解释:【答案】C。解析：设这批树苗一共有z棵，从“小王每天种8棵，第21天种完”可知，8×20+l≤z≤8×21；从“小李每天种9棵，第18天种完”可知，9×17+1≤z≤9×18，结合两个不等式得：161≤z≤162。如果小孙每天种10棵的话，在z的取值范围内，一定是在第17天种完。

55、从装满1000克浓度为50%的酒精瓶中倒出200克酒精，再倒入蒸馏水将瓶加满。这样反复三次后，瓶中的酒精浓度是多少_____
A: 22.5%B: 24.4%C: 25.6%D: 27.5%
参考答案: C 本题解释:【解析】C。每次操作后，酒精浓度变为原来的，因此反复三次后浓度变为。

56、四个相邻质数之积为17 017,他们的和为_____。
A: 48B: 52C: 61D: 72
参考答案: A 本题解释:【答案】A。解析:l7017=l7×l3×11×7,它们的和为48。

57、小王的手机通讯录上有一手机号码，只记下前面8个数字为15903428。但他肯定，后面3个数字全是偶数，最后一个数字是6，且后3个数字中相邻数字不相同，请问该手机号码有多少种可能?_____
A: 15B: 16C: 20D: 185
参考答案: B 本题解释:【答案】B。解析：一位偶数有0、2、4、6、8，共5个。考虑倒数第二位，因为相邻数字不相同且为偶数，则有4种选择。倒数第三位与倒数第二位不相同，也有4种选择，共有4×4=16种情况。

58、从一楼走到五楼，爬完一层休息30秒，一共要210秒，那么从一楼走到7楼，需要多少秒_____
A: 318B: 294C: 330D: 360
参考答案: C 本题解释:答案：C 解析：从一点走到五楼，休息了三次，那么每爬上一次需要的时间为（210-30×3）÷（5-1）=30秒，故从一楼走到七楼需要30×（7-1）+30×（7-2）=330秒。

59、某人上午8点要上班，可是发现家里的闹钟停在了6点10分，他上足发条但忘了对表就急急忙忙的上班去了，到公司一看还提前了10分钟。中午12点下班后，回到家一看，闹钟才11点整，假定此人上班、下班在路上用的时间相同，那么他家的闹钟停了多少分钟?_____
A: 100B: 90C: 80D: 70
参考答案: C 本题解释:【解析】C。由题意知：6时10分+闹钟停的时间=7时50分;11时+闹钟停的时间=12时+下班后路上走的时间，所以闹钟停的时间+上班时间=7时50分-6时10分=100分钟，闹钟停的时间上班时间=12时-11时=60分，故闹钟停的时间为（100+60）÷2=80分钟。

60、六位同学数学考试的平均成绩是92.5分，他们的成绩是互不相同的整数，最高分是99分，最低分是76分，则按分数从高到低居第三位的同学至少得多少分_____。
A: 93B: 94C: 95D: 96
参考答案: C 本题解释:C。本题为构造类题目。总分为92.5×6=555，去掉最高分和最低分后还有555-99-76=380。要使第三名分尽可能的低，首先第二名分要尽可能高，即为98分(还余282分)。而第四和第五名的分数要尽量的高，与第三名的分最接近，三者的分为93，94，95。那么最高分至少为95。所以选择C选项。

61、有一件工作，丙单独做需10小时完成;乙、丙合作需4小时完成。甲2小时完成的工作量，乙需要3小时才能完成。现在这件工作由丙独做，他从清晨5时开工，必须在中午12时完工。甲、乙二人应帮助丙工作多少时间才能使丙准时完成工作?_____
A: 4/5小时B: 1小时C: 4/3小时D: 2小时
参考答案: A 本题解释:

62、红星小学组织学生排成队步行去郊游,每分钟步行60米,队尾的王老师以每分钟步行150米的速度赶到队头,然后立即返回队尾,共用10分钟。求队伍的长度。_____
A: 630米B: 750米C: 900米D: 1500米
参考答案: A 本题解释:【答案】A。解析:设王老师从队尾走到队头用x分钟,可列方程(150-60)×x=(150+60)×(10-x),解得x=7分钟,则队伍的长度为(150-60)×7=630米,选择A。

63、减数、被减数与差三者之和除以被减数，商是多少_____
A: 0B: 1C: 2D: 减数与差之和
参考答案: C 本题解释: 【解析】C。减数+被减数+差=2被减数，所以商为2。

64、混合并购是指一个企业对那些与自己生产的产品不同性质和种类的企业进行并购的行为，其中目标公司与并购企业既不是同一行业，又没有纵向关系。根据上述定义，下列属于混合并购的是_____。
A: 某碳酸饮料公司收购了一家灌装公司和一家饼干公司B: 某网站收购了一家户外传媒公司和一家网络游戏公司C: 某出版集团收购了一家印刷厂和一家文学网站D: 某电脑集团收购了一家酒厂和一家葡萄庄园
参考答案: D 本题解释:定义的关键信息是“目标公司与并购企业既不是同一行业，又没有纵向关系”。A项，灌装公司可以为饮料提供包装，因此和并购企业存在纵向关系，而饼干公司则和碳酸饮料公司都属于食品行业。B项，网站属于互联网传媒，因此网站和户外传媒属于同一行业；同时，网站也可能提供网络游戏，因此网站与网络游戏公司也可能存在纵向关系。C项，印刷是出版的一道流程，因此印刷厂和出版集团存在纵向关系。D项，酒厂和葡萄庄园虽然有可能存在纵向关系，但是二者与并购企业——电脑集团的产品性质完全不同，且不存在任何关系，因此选D。

65、甲、乙、丙三人的平均年龄是26岁，除去丙后，甲、乙两人平均年龄是24岁，丙的年龄是多少岁?_____
A: 26B: 28C: 30D: 32
参考答案: C 本题解释:C解析：设甲、乙、丙年龄分别为x、y、z，根据题意得：(x+y+z)/3=26(x+y)/2=24，解得：z=30，选C。

66、光的速度是每秒30万千米,太阳离地球1亿5千万千米。问:光从太阳到地球要用几分钟?_____
A: 83B: 12C: 7.2D: 20
参考答案: A 本题解释:【答案】A。解析:150000000÷300000÷60=150÷3÷6=50÷6=8.3(分)。故应选择A。

67、一个质数的3倍与另一个质数的2倍之和等于20，那么这两个质数的和是_____。
A: 8 　 B: 9 　 C: 7 　 　D: 6
参考答案: B 本题解释:【解析】B。 设这两个质数分别为x、y,则3x+2y=20。2y和20都是偶数，则3x也是偶数，即x为偶数。又因为x同时是质数，则x=2，y=7。两质数之和x+y=9。故选B。

68、父亲和儿子的年龄和为50岁，三年前父亲的年龄是儿子的三倍，多少年后儿子年满18岁?_____
A: 2B: 4C: 6D: 8
参考答案: 本题解释:B【解析】设x年后儿子年满18岁，则儿子现在的年距为18-x，父亲为50-（18-x）=32+x，根据题意得：3（18-x-3）=32+x-3，解得x=4，故正确答案为B。

69、有一批书要打包后邮寄，要求每包内所装书的册数都相同，用这批书的7/12打了14个包还多35本，余下的书连同第一次多的零头刚好又打了11包，这批书共有多少本?_____
A: 1000B: 1310C: 1500D: 1820
参考答案: C 本题解释: C 解析： 由已知条件，全部书的7/12打14包还多35本，可知全部书的1/12打2包还多5本，即全部书的5/12打10包还多25本，而余下的是5/12加35本打11包。所以，（35+25）÷（11-10）=60本，1包是60本，这批书共有（14+11）×60=1500（本）。故本题正确答案为C。

70、一单位组织员工乘坐旅游车去泰山，要求每辆车上的员工人数相等。起初，每辆车上乘坐22人，结果有1人无法上车；如果开走一辆空车，那么所有的游客正好能平均乘到其余各辆旅游车上，已知每辆车上最多能乘坐32人。请问该单位共有多少员工去了泰山？_____
A: 269B: 352C: 478D: 529
参考答案: D 本题解释:D。开走一辆空车，则剩余22+1=23人，需要把23人平均分配到剩余的旅游车上。23的约数只有23和1，而每辆车最多能乘坐32人，排除将23人分配到1辆车上的情况（22+23>32），只能每辆车上分配1人，分配后每辆车有22+1=23人。进行条件转换，如果没有开走那辆车，那么每辆车分配23人，还少23人，加上已有条件“每辆车上乘坐22人，结果有1人无法上车”，就转化成了常规的盈亏问题。有车（1+23）÷（23-22）=24辆。有员工24×22+1=529人。

71、某计算机厂要在规定的时间内生产一批计算机，如果每天生产140台，可以提前3天完成;如果每天生产120台，就要再生产3天才能完成。问规定完成的时间是多少天?_____
A: 30B: 33C: 36D: 39
参考答案: D 本题解释:答案：D【解析】解答此题可以同时使用代入法和方程法。为快速解题可首先考虑方程法，设规定时间为x天，则（x-3）×l40=（x+3）×l20，解得x=39。故选D。

72、三边长均为整数且最大边长为2009的三角形共有多少个？_____
A: 1008016 B: 1009020 C: 1010025 D: 2019045
参考答案: C 本题解释: C。根据三角形的构成原理，可知最大边长为2009时，另两边的和大于2009，差小于2009，则两边≤2009且≥1，则可知介于最长边与最短边之间的那条中边的长度必≥1005且≤2009。中边为1005时，另一边=1005，1种可能；中边为1006时，另一边=1004，1005，1006，共3种可能；中边为1007时，另一边=1003，1004，1005，1006，1007，共5种可能；……中边为2009时，另一边=1~2009，共2009种可能。因此三角形总和=1+3+5+…+2007+2009=1005（1+2009）/2=1010025种。所以答案为C项。

73、某单位职工24人中，有女性11人，已婚的16人。在已婚的16人中有女性6人。问这个单位的未婚男性有多少人？_____
A: 1B: 3C: 9D: 12
参考答案: B 本题解释:B。易知该单位有男性13人，其中已婚的有10人，故未婚的有3人，选B。

74、一根钢管，如果把它锯成4段，需要24分钟。照此速度，如果将它锯成8段，需要多长时间？_____
A: 42分钟B: 48分钟C: 56分钟D: 64分钟
参考答案: C 本题解释:【答案】C。解析：把一根钢管锯成4段有3个切口，并且需要24分钟，一个切口需要8分钟。若将它锯成8段，将有7个切口，则一共需要7×8＝56分钟。故正确答案为C。

75、(101+103+…+199)-(90+92+…+188)=_____。
A: 100　B: 199　C: 550　D: 990
参考答案: C 本题解释:C[解析]提取公因式法。101-90=11，103-92=11，……，199-188=11，总计有50个这样的算式，所以50×11=550，选择C。

76、旅行社对120人的调查显示，喜欢爬山的与不喜欢爬山的人数比为5：3;喜欢游泳的与不喜欢游泳的人数比为7：5;两种活动都喜欢的有43人。对这两种活动都不喜欢的人数是_____。
A: 18B: 27C: 28D: 32
参考答案: A 本题解释:【答案】A。解析：依题意喜欢爬山的有75人，喜欢游泳的有70人，由容斥原理公式，两种活动都不喜欢的有120-(75+70-43)=18人。

77、某路公共汽车，包括起点和终点共有15个车站，有一辆车除终点外，每一站上车的乘客中，恰好有一位乘客到以后的每一站下车，为了使每位乘客都有座位，问这辆公共汽车最少要有多少个座位？_____。
A: 53 B: 54C: 55 D: 56
参考答案: D 本题解释:D

78、甲、乙两地相距100千米，张先骑摩托车从甲出发，1小时后李驾驶汽车从甲出发，两人同时到达乙地。摩托车开始速度是50千米/小时，中途减速为40千米/小时。汽车速度是80千米/小时。汽车曾在途中停驶10分钟，那么张驾驶的摩托车减速时是在他出发后的多少小时?_____
A: 1B: 1(1/2)C: 1/3D: 2
参考答案: C 本题解释: C 解析： 汽车行驶100千米需100÷80=1（1/4）（小时），所以摩托车行驶了1（1/4）+1+1/6=2（5/12）（小时）。如果摩托车一直以40千米/小时的速度行驶，2（5/12）小时可行驶9623千米，与100千米相差10/3千米。所以一开始用50千米/小时的速度行驶了10/3÷（50-40）=1/3（小时）。故本题选C。

79、A、B、C、D四支球队开展篮球比赛，每两个队之间都要比赛1场，已知A队已比赛了3场，B队已比赛了2场，C队已比赛了1场，D队已比赛了几场？（）
A: 3B: 2C: 1
参考答案: B 本题解释:每个球队要比赛3场，则A队和B队、C队、D队各比赛1场，C队和A队比赛1场，B队和A队、D队各比赛1场，故D队比赛了2场。所以选B。

80、用1，2，3，4，5这五个数字组成没有重复数字的自然数，从小到大顺序排列：1，2，3，4，5，12，……，54321。其中，第206个数是_____
A: 313 B: 12345 C: 325 D: 371
参考答案: B 本题解释:B。由1、2、3、4、5组成的没有重复数字的一位数共有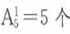；二位数共有个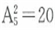；三位数共有个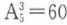；四位数共有个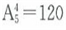；至此由1、2、3、4、5组成的没有重复数字的四位以内的数共有5+20+60+120=205个；那么第206个数是第一个由1、2、3、4、5组成的五位数，即最小的五位数12345。

81、8.01×1.24+8.02×1.23+8.03×1.22的整数部分是多少?_____
A: 24B: 27C: 29D: 33
参考答案: C 本题解释:答案：C【解析】由8.03×1.22<8.02×1.23<8.01×1.24得：8.01×1.24+8.02×1.23+8.03×1.22<8.01×1.24×3<8×1.25×3=30。8.01×1.24+8.02×1.23+8.03×1.22>8×（1.24+1.23+1.22）=8×3.69=29.52。所以，所求的整数部分为29。故选C。

82、某年10月份有四个星期四,五个星期三,这年的10月8日是星期_____。
A: 一B: 二C: 三D: 四
参考答案: A 本题解释:【答案】A。解析:根据题意,10月份的31号肯定是星期三,以此推断10月10号也是星期三,那么10月8日应该是星期一。

83、一杯糖水，第一次加入一定量的水后，糖水的含糖百分比为15%;第二次又加入同样多的水，糖水的含糖量百分比为12%;第三次加入同样多的水，糖水的含糖量百分比将变为多少? _____
A: 8%B: 9%C: 10%D: 11%
参考答案: C 本题解释:C。【解析】设第一次加入糖水后，糖水的量的为100，则糖的量为15，第二次加水后，糖水的量为15/12*100=125，即加水的量为125-100=25，第三次加水，百分比为15/（125+15）=10%

84、四个相邻质数之积为17017，他们的和为_____
A: 48B: 52C: 61D: 72
参考答案: A 本题解释:答案：A【解析】17017分解因数为17×13×11×7，他们的和为48。

85、某班共有50名学生参加数学和外语两科考试，已知数学成绩及格的有40人，外语成绩及格的有25人，据此可知数学成绩及格而外语成绩不及格者_____。
A: 至少有10人B: 至少有15人C: 有20人D: 至多有30人
参考答案: B 本题解释:B【解析】这是一个集合问题，首先可排除答案D，因为与已知条件“外语及格25人”即“外语不及格25人”不符;其次排除C，因为仅以外语及格率为50%推算数学及格者（40人）中外语不及格人数为40×50%=20（人），缺乏依据，实际上，数学及格者中外语不及格的人数至少为25-（50-40）=15人，答案为B。

86、某团体有100名会员，男、女会员人数比为14∶11，会员分为三组，甲组人数与乙、丙两组人数总和一样多，甲、乙、丙各组男女会员的人数比是甲为12∶13，乙为5∶3，丙为2∶1。求丙组中有男会员多少人?_____
A: 20人B: 14人C: 12人D: 10人
参考答案: C 本题解释:C【解析】由“甲组人数与乙丙两组人数总和一样多”可知，甲组有会员100×1/2=50（人）。全体男会员有100×14/（14+11）=56人，甲组中有男会员50×1212+13=24人，乙、丙两组共有男会员56-24=32人。乙组中男会员占58，丙组中男会员占23。假若丙组中男会员也占58，则乙、丙两组共有男会员50×58=2508人，比32人少了（32-2508）人。这样就可以求出丙组中总的人数为（32-2508）÷（23-58）=18人，则丙组男会员有18×23=12人。

87、小明前三次数学测验的平均分数是88分，要想平均分数达到90分以上，他第四次测验至少要达到_____
A: 98分B: 96分C: 94分D: 92分
参考答案: B 本题解释: 【解析】B。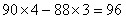分，该数值可以根据以上式子判定尾数为6，选择B。

88、将一块三角形绿地沿一条直线分成两个区域，一块为三角形，一块为梯形，已知分出的三角形区域的面积为1.2亩，梯形区域的上、下底边分别为80米、240米，问分出的梯形区域的面积为多少亩?_____
A: 9.6B: 11.2C: 10.8D: 12.0
参考答案: A 本题解释:本题答案选A。解析：分出的三角形面积为1.2亩＝800平方米，底边为梯形的上底边80米可知三角形的高为800×2÷80＝20米，整块三角形绿地的底边为240米，由比例关系可得，高为20÷（80÷240）＝60米，则绿地面积为240×60÷2＝7200平方米＝10.8亩，故梯形面积为10.8-1.2＝9.6亩。

89、筑路队原计划每天筑路720米，实际每天比原计划多筑路80米，这样在规定完成全路修筑任务的前3天，就只剩下1160米未筑，这条路全长多少千米?_____
A: 8.10B: 10.12C: 11.16D: 13.50
参考答案: C 本题解释:C解析：现在每天筑路：720+80=800（米）规定时间内，多筑的路是：（720+80）×3-1160=2400-1160=1240（米）求出规定的时间是1240÷80=15.5（天），这条路的全长是,720×15.5=11160（米）。故本题选C。

90、一次数学考试共有20道题，规定：答对一题得2分，答错一题扣1分，未答的题不计分。考试结束后，小明共得23分，他想知道自己做错了几道题，但只记得未答的题的数目是个偶数。请你帮助小明计算一下，他答错了多少道题_____
A: 3B: 4C: 5D: 6
参考答案: A 本题解释:【答案】A，代入即可，答对13道题，得26分，打错3道扣3分，未答的题的数目是4道恰好是个偶数。

91、2007年4月20日，上证综指早盘高开11点，以3460.90点开盘后，随即逐波上扬，至终盘报收于3584.20点，较上一个交易日上涨了_____
A: 3.56% B: 11点 C: 113.70点 D: 134.30点
参考答案: D 本题解释: 【解析】较上一个交易日上涨多少应该以上个交易日收盘点数为准，所以高开的11点依然属于今天上涨的部分，故有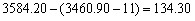点。故选D。

92、一个学雷锋小组的大学生们每天到餐馆打工半小时，每人可挣3元钱。到11月11日，他们一共挣了1764元。这个小组计划到12月9日这天挣足3000元捐给“希望工程”。因此小组必须在几天后增加一个人。增加的这个人应该从11月_____日起每天到餐馆打工，才能到12月9日恰好挣足3000元钱。
A: 18B: 24C: 14D: 20
参考答案: D 本题解释:D[解析]还缺3000-1764=1236（元），从11月12日～12月9日还有30+9-12+1=28（天），这28天中，（原来小组中）每人可挣3×28=84（元）。因为1236÷84=14……60，所以原有14人，必须增加一个人挣60元。60÷3=20（天），30+9-20+1=20，所以增加的这个人应该从11月20日起去打工。

93、三位采购员定期去某市场采购，小王每隔9天去一次，大刘每隔6天去一次，老杨每隔7天去一次，三人星期二第一次在这里碰面，下次相会将在星期几?_____
A: 星期一B: 星期五C: 星期二D: 星期四
参考答案: C 本题解释:C解析：此题乍看上去是求9，6，7的最小公倍数的问题，但这里有一个关键词，即“每隔”，“每隔9天”也即“每10天”，所以此题实际上是求10，7，8的最小公倍数。既然该公倍数是7的倍数，那么肯定下次相遇也是星期二。(10，7，8的最小公倍数是5×2×7×4=280。280÷7=40，所以下次相遇肯定还是星期二。)

94、7个同学排成两排照相，前排3人，后排4人，共有_____种站法。
A: 1680B: 2400C: 2520D: 5040
参考答案: D 本题解释:【解析】相当于把7个元素放在预先指定好的7个不同位置上，因此，是7个同学的全排列，共有P77=5040种站法。

95、一本100多页的书，被人撕掉了4张，剩下的页码总和为8037，则该书最多有多少页？_____
A: 134B: 136C: 138D: 140
参考答案: A 本题解释:【答案】A。解析：撕掉一张纸，其正反两面的两个页码之和为奇数，则撕掉4张，页码总数必为偶数，剩余页码和为8037，所以原书的页码总和必然为奇数，由此排除BD（BD选项能被4整除，而连续4页的页码和必然为偶数）。代入C，可知整书的页码总和为（1＋138）÷2×138＝9591，于是撕掉的页码和为9591－8037＝1554，那么撕掉的8页的页码平均值为194.25，显然与最多138页矛盾。故正确答案为A。

96、某乐队举办一场演唱会的收入是7000元，乐队的主唱分得其中的25%，另外5名成员平分余下的收入，那么他们每人分得多少元？_____
A: 1750B: l400C: 1120D: 1050
参考答案: D 本题解释:【解析】D。另外5名成员平分余下的收入，每人拿15%，即1050元。

97、阳光下，电线杆的影子投射在墙面及地面上，其中墙面部分的高度为1米，地面部分的长度为7米。甲某身高1.8米，同一时刻在地面形成的影子长0.9米。则该电线杆的高度为_____。
A: 12米B: 14米C: 15米D: 16米
参考答案: C 本题解释:【答案】C。解析：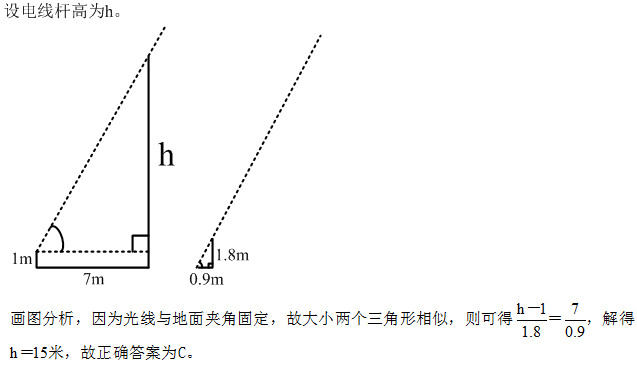

98、某中介服务机构根据服务项目所涉及的金额分段按一定比例收取服务费，具体标准如下：1万元(含)以下收取50元;1万元以上、5万元(含)以下的部分收取3%;5万元以上、10万元(含)以下的部分收取2%.(如某一服务项目所涉及金额为5万元时，应收取服务费1250元。)现有一服务项目所涉及金额为10万元，那么，所收取的服务费应为：_____
A: 2250元B: 2500元C: 2750元D: 3000元
参考答案: A 本题解释:A。【解析】分段按比例计算，选A。

99、一条长度为30米、宽度为3米的未划停车位的路边，最差的情况也可以停2米宽、3米长的汽车多少辆?_____
A: 5辆B: 7辆C: 8辆D: l5辆
参考答案: A 本题解释:【解析】分三种情况:第一种:汽车如果与道路垂直。每辆车的车距应尽可能的大，但距离必须小于2米（否则可以再停一辆），当两辆车的车距为2米时，最少可停（30-2）÷（2+2）=7（辆），那么最差的情况下至少可以停8辆车;第二种:汽车如果与道路平行。每辆车的车距应尽可能的大，但距离小于3米，当两辆车的车距为3米时，最少可停（30-3）÷（3+3）=4.5（辆），即停5辆。第三种:汽车与道路有平行与垂直两种情况并存，则停的汽车数量应介于5辆和8辆之间。而题干是问的最差的情况，故最少停5辆车。

100、在一次国际美食大赛中，中、法、日、俄四国的评委对一道菜品进行打分。中国评委和法国评委给出的平均分是94，法国评委和日本评委给出的平均分是90，日本评委和俄罗斯评委给出的平均分是92，那么中国评委和俄罗斯评委给出的平均分是_____。
A: 93分B: 94分C: 96分D: 98分
参考答案: C 本题解释:C【解析】设中、法、日、俄四国的评委给出的分数分别是A、B、C、D，根据题意可知：A+B=94×2，B+C=90×2，C+D=92×2，又因为A+D=（A+B）+（C+D）-（B+C）=94×2+92×2-90×2=（94+92-90）×2=96×2所以中国评委和俄国评委给出的平均分是96分，本题正确答案为C。