微信搜索关注"91考试网"公众号,领30元,获取公务员、事业编、教师等考试资料40G!
1、单选题 三位数的自然数N满足:除以6余3,除以5余3,除以4也余3,则符合条件的自然数N有几个?_____
A: 8
B: 9
C: 15
D: 16
参考答案: C
本题解释:正确答案是C考点余数与同余问题解析由题意可知满足同余情形,例如此题”三位自然数N除以6余3,除以5余3,除以4也余3”,可见余数恒为3,则取3,因此N的表达式为60n+3,其中60为6、5、4的最小公倍数,根据题目中的N为三位数,可得不等式100≤60n+3≤999,解得2≤n≤16,因此符合条件的自然数有15个,故正确答案为C选项。注:同余问题需要如下口诀:余同取余,和同加和,差同减差,最小公倍数做周期。口诀解释:余同取余,例如本题,余数恒为3,则取3;合同加和,例如”一个数除以7余1,除以6余2,除以5余3”,可见除数与余数的和相同,取此和8,被除数的表达式为210n+8;差同减差,例如”一个数除以7余3,除以6余2,除以5余1”。可见除数和余数的差相同,取此差4,被除数的表达式为210-4,其中210为5、6、7的最小公倍数。秒杀技根据题目,符合要求的数出现的周期为6、5、4的最小公倍数60,也即每60个连续自然数中必然有一个符合要求,三位数共有900个,因此符合要求的三位数共有900÷60=15(个),故正确答案为C选项。标签最小公倍数同余问题
2、单选题 开运动会时,高一某班共有28名学生参加比赛,有15人参加游泳比赛,有8人参加田径比赛,有14人参加球类比赛,同时参加游泳和田径比赛的有3人,同时参加游泳和球类比赛的有3人,没有人同时参加三项比赛。问同时参加田径和球类比赛的有多少人?_____
A: 1
B: 2
C: 3
D: 4
参考答案: C
本题解释:参考答案:C
题目详解:解法一:根据题意,设:参加游泳为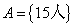
3、单选题 在1至100这100个数中,有既不能被5整除也不能被9整除的数,它们的和是_____。
A: 1644
B: 1779
C: 3406
D: 3541
参考答案: D
本题解释:【答案解析】先求出被5或9整除的数的和。1至100中被5整除的数有5,10,15,…,100,和为5+10+15+…+100=(100+5)×20÷2=10501至100中被9整除的数有9,18,…,99,和为9+18+27+…+99=(9+99)×11÷2=594又因为1~100中,45,90这两个数同时被5与9整除,于是所求的和是(1+2+…+100)-(5+10+…+100)-(9+18+…+99)+(45+90)=3541。因此,本题正确答案为D。
4、单选题 现有50名学生都做物理、化学实验,如果物理实验做正确的有40人,化学实验做正确的有31人,两种实验都做错的有4人,则两种实验都做对的有_____。
A: 27人
B: 25人
C: 19人
D: 10人
参考答案: B
本题解释:参考答案:B
题目详解:解法一:A={{物理实验做正确的人}};B={{化学实验做正确的人}}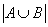
5、单选题 (2003广东,第9题)从装满100克浓度为  A:
A: 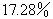 B:
B:  C:
C: 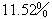 D:
D: 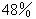 参考答案: A
参考答案: A
本题解释:参考答案:A
题目详解:根据题意:每次操作后,酒精浓度变为原来的(100-40)/100=0.6;故反复三次后浓度变为:80%×0.6×0.6×0.6=17.28%;所以,选A。考查点:数量关系>数学运算>浓度问题>不同溶液混合