1、单选题  公路上有三辆同向行驶的汽车，其中甲车的时速为63公里，乙、丙两车的时速均为60公里，但由于水箱故障，丙车每连续行驶30分钟后必须停车2分钟。早上10点，三车到达同一位置，问1小时后，甲、丙两车最多相距多少公里?_____
A: 5
B: 7
C: 9
D: 11
参考答案: B
本题解释:正确答案是B考点行程问题解析在这1个小时中，丙车最多休息4分钟，也即丙在一个小时内最少行程为60×56÷60=56公里。而甲车持续行驶，可达63公里。因此两车最多相距7公里，故正确答案为B。

2、单选题  甲、乙两人在长30米的泳池内游泳，甲每分钟游37.5米，乙每分钟游52.5米，两人同时分别从泳池的两端出发，触壁后原路返回，如是往返。如果不计转向的时间，则从出发开始计算的1分50秒内两人共相遇了多少次?_____
A: 2
B: 3
C: 4
D: 5
参考答案: B
本题解释:正确答案是B考点行程问题解析解析1：题目的关键在于第一次相遇，两人游过长度之和为泳池长，之后每次相遇，都需要两人再游过两个泳池长。两人一起游一个泳池长，所需时间为30÷(37.5+52.5)×60=20(秒)，因此两人分别在20秒时、60秒时、100秒时相遇，共相遇3次。故正确答案为B。解析2：关键点同解析1。直接求出1分50秒两人合起来游过的距离为(37.5+52.5)×110÷60=165(米)，为5.5个泳池长。而两人相遇时都恰是合起来游过距离为奇数个泳池长时，也即两人分别在合游1个、3个、5个泳池长时相遇，故共相遇3次。故正确答案为B。解析3：套用公式。先看迎面相遇，30×(2N-1)≤(37.5+52.5)×11/6，得N≤3.25，即有3次迎面相遇;再看追上相遇，30×(2N-1)≤(52.5-37.5)×11/6，得N≤23/24，即没有追及相遇。故总的相遇次数为3次。故正确答案为B。公式：两运动体从两端同时出发，相向而行，不断往返：第N次迎面相遇，两运动体路程和=全程×(2N-1);第N次追上相遇，两运动体路程差=全程×(2N-1)。标签公式应用

3、单选题  小张、小王二人同时从甲地出发，驾车匀速在甲乙两地之间往返行驶。小张的车速比小王快，两人出发后第一次和第二次相遇都在同一地点，那么小张的车速是小王的_____倍。
A: 1.5
B: 2
C: 2.5
D: 3
参考答案: B
本题解释:正确答案是B考点行程问题解析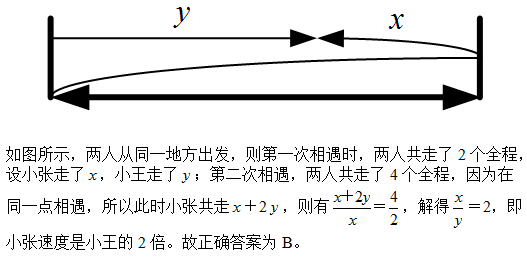

4、单选题  甲、乙、丙三辆车的时速分别为60公里、50公里和40公里，甲从A地，乙和丙从B地同时出发相向而行，途中甲遇到乙后15分钟又遇到丙，问A、B两地相距多少公里?_____
A: 150公里
B: 250公里
C: 275公里
D: 325公里
参考答案: C
本题解释:正确答案是C考点行程问题解析解析1：甲乙相遇时，甲走了全程的60÷(50+60)=6/11;甲丙相遇时，甲走了全程的60÷(40+60)=6/10;在甲乙相遇之后到甲丙相遇，甲走了全程的6/10-6/11=3/55，这段路程为60×15/60=15(公里)，所以AB相距15÷(3/55)=275(公里)。解析2：设AB相距s公里，则s/(60+50)=s/(60+40)-1/4，解得s=275(公里)。故正确答案为C。

5、单选题  A: A
B: B
C: C
D: D
参考答案:
本题解释:正确答案是B考点行程问题解析