1、单选题  旅客携带了30公斤行李从A地乘飞机去B地，按民航规定，旅客最多可免费携带20公斤行李，超重部分每公斤按飞机票价格的1.5%购买行李票，现该旅客购买了120元的行李票，则他的飞机票价格应是多少？_____
A: 10000           
B: 800           
C: 600           
D: 400
参考答案: B
本题解释:【解析】B。行李超重部分每千克收取120÷（30－20）＝12元，则飞机票价为12÷1.5％＝800元。

2、单选题  往一个圆柱形容器里注水，已知容器底面半径为10cm，高为40cm，当注入水柱高为H，水柱高由低到高变化时，水柱体积V(cm²)也随之发生变化，下列说法中，不正确的是_____。
A: V与H都是变量
B: H是自变量，V是因变量
C: V与H的关系可为V=100πH
D: V=150立方厘米时，H=25厘米
E: 当H是40厘米时，V达到最大值为4000π，此时不能再注入水
参考答案: D
本题解释:正确答案是D考点几何问题解析

3、单选题  一个班里有30名学生，有12人会跳拉丁舞，有8人会跳肚皮舞，有10人会跳芭蕾舞。问至多有几人会跳两种舞蹈?_____
A: 12人
B: 14人
C: 15人
D: 16人
参考答案: C
本题解释:正确答案是C考点统筹规划问题解析要使会跳两种舞蹈的人最多，则尽量在三种舞蹈之间进行匹配，使得两两匹配的人数之和最多。因此就不能将一种舞蹈只与另一种舞蹈进行全额匹配，例如不能将会跳肚皮舞的8人全部与拉丁舞匹配。实际上，为实现两两匹配的最多，则每组用于匹配的人数应相等或接近。从最少人数出发，会跳肚皮舞的8人，将其划分时要考虑拉丁舞和芭蕾舞人数相差2，故在划分此8人时注意这一点，可将8人划分为5人和3人。其中5人除了会肚皮舞之外，还会拉丁舞;3人会肚皮舞之外还会芭蕾舞。此时拉丁舞与芭蕾舞还各自剩7人、7人，又可以匹配得到7人既会拉丁舞又会芭蕾舞。会跳两种舞的人数至多为15人。故正确答案为C。秒杀技假定拉丁+肚皮、肚皮+芭蕾、芭蕾+拉丁的人数分别为x、y、z，则根据题意可知x+y≤8，x+z≤12，y+z≤10，求取x+y+z的最大值。对于前述三个不等式，先将不等号变为等号尝试求解一下，恰好可得x=5，y=3，z=7，代回验证可知所有条件均满足。因此可知x+y+z的最大值为15。故正确答案为C。标签构造调整

4、单选题  现有式样、大小完全相同的四张硬纸片，上面分别写了1、2、3、4四个不同的数字，如果不看数字，连续抽取两次，抽后仍旧放还，则两次都抽到2的概率是_____。
A: 1/2
B: 1/4
C: 1/8
D: 1/16
参考答案: D
本题解释:【解析】两次都抽到2的概率是1/4*1/4=1/16，选D。

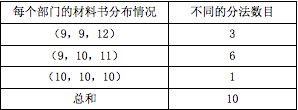
5、单选题  某单位订阅了30份学习材料发放给3个部门，每个部门至少发放9份材料。问一共有多少种不同的发放方法?_____
A: 7
B: 9
C: 10
D: 12
参考答案: C
本题解释:正确答案是C考点排列组合问题解析