1、单选题  若p和q为质数，且5p+3q=91，则p和q的值为：_____
A: 2，27
B: 3，19
C: 5，17
D: 17，2
参考答案: D
本题解释:参考答案
题目详解:5p+3q=91，∴p、q为一奇一偶，∵p和q为质数，∴p、q中必有一数为2，当p=2时，q=27，27为合数，故舍去，当q=2时，p=17。故p=17，q=2。故答案为：17，2。考查点:数量关系>数学运算>计算问题之数的性质>奇偶性与质合性问题>奇偶性

2、单选题  如下图所示，正方形ABCD的边长为5cm，AC、BD分别是以点D和点C为圆心、5cm为半径作的圆弧。问阴影部分a的面积比阴影部分b小多少?_____(π取3.14)A: 13.75平方厘米
B: 14.25平方厘米
C: 14.75平方厘米
D: 15.25平方厘米
参考答案: B
本题解释:正确答案：B解析：本题考查几何问题。两个空白部分面积相等，设每个空白部分的面积为c，则有：b+c=1/4•πr^2,a+c=5^2-1/4•πr^2，解方程得到b-a=14.25cm。故答案为B。

3、单选题  小木、小林、小森三人去看电影，如果用小木带的钱去买三张电影票，还差0.55元;如果用小林带的钱去买三张电影票，还差0.69元;如果用三人带去的钱买三张电影票，就多0.30元，已知小森带了0.37元，那么买一张电影票要用多少元?_____
A: 1.06
B: 0.67
C: 0.52
D: 0.39
参考答案: D
本题解释:D【解析】设每张电影票x元，则小木的钱数为3x-0.55元，小林的钱数为3x-0.69元，小森的钱数为0.37元。三人的钱数和为3x+0.30元，即可得出：3x-0.55+3x-0.69+0.37=3x+0.30，求得x=0.39（元）。

4、单选题  在前100个自然数中，能被3除尽的数相加，所得到的和是多少?_____
A: 1250
B: 1683
C: 1275
D: 1400
参考答案: B
本题解释:参考答案:B本题得分:
题目详解:根据题意，在前100中，能被3除尽的数，即个位数字之和为3的倍数;“在前100个自然数中，能被3整除的数”有3、6、9、12、15、18……故可以转化为首项为3，末项为99，公差为3，共有33项的等差数列;在前100个自然数中，能被3除尽的数的和——等差数列求和：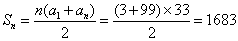

5、单选题  某种考试已举行了24次，共出了试题426道，每次出的题数有25题，或者16题，或者20题，那么其中考25题的有多少次?_____
A: 4 
B: 2 
C: 6 
D: 9
参考答案: B
本题解释:B【解析】 假设24次考试，每次16题，则共考16×24=384（道），比实际考题数少426-384=42（道），也就是每次考25题与每次考20题，共多考的题数之和为42道。而考25题每次多考25-16=9（道），考20题每次多考20-16=4（道）。这样有9×A+4×B=42，其中A表示考25题的次数，B表示考20题的次数。根据数的奇偶性可知，B无论是奇数还是偶数，4B总是偶数，那么9A也是偶数，因此A必定是偶数，且A不是2就是4。如果A=4，则9×4+4×B=42，B=1.5不合题意，应删去，所以考25道试题的次数是2次。