微信搜索关注"91考试网"公众号,领30元,获取公务员、事业编、教师等考试资料40G!
sp; [ ]
(9)设函数y=y(x)由参数方程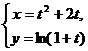 确定,则曲线y=y(x)在x=3处的法线与x轴交点的横坐标是
确定,则曲线y=y(x)在x=3处的法线与x轴交点的横坐标是
(A) 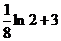 . (B)
. (B) 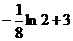 .
.
(C) 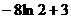 . (D)
. (D) 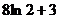 . [ ]
. [ ]
(10)设区域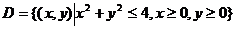 ,f(x)为D上的正值连续函数,a,b为常数,则
,f(x)为D上的正值连续函数,a,b为常数,则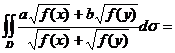
(A) 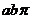 . (B)
. (B) 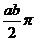 . (C)
. (C) 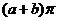 . (D)
. (D) 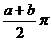 . [ ]
. [ ]
(11)设函数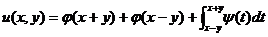 , 其中函数
, 其中函数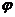 具有二阶导数,
具有二阶导数,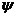 具有一阶导数,则必有
具有一阶导数,则必有
(A) 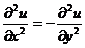 . (B)
. (B) 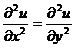 .
.
(C) 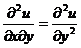 . (D)
. (D) 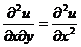 . [ ]
. [ ]
(12)设函数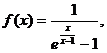 则
则
(A) x=0,x=1都是f(x)的第一类间断点.
(B) x=0,x=1都是f(x)的第二类间断点.
(C) x=0是f(x)的第一类间断点,x=1是f(x)的第二类间断点.
x=0是f(x)的第二类间断点,x=1是f(x)的第一类间断点. [ ]
(13)设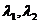 是矩阵A的两个不同的特征值,对应的特征向量分别为
是矩阵A的两个不同的特征值,对应的特征向量分别为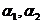 ,则
,则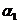 ,
,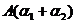 线性无关的充分必要条件是
线性无关的充分必要条件是
(A) 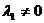 . (B)
. (B) 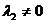 . (C)
. (C) 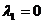 . (D)
. (D) 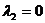 . [ ]
. [ ]
(14)设A为n(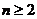 )阶可逆矩阵,交换A的第1行与第2行得矩阵B,
)阶可逆矩阵,交换A的第1行与第2行得矩阵B, 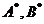 分别为A,B的伴随矩阵,则
分别为A,B的伴随矩阵,则
(A) 交换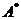 的第1列与第2列得
的第1列与第2列得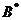 . (B) 交换
. (B) 交换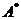 的第1行与第2行得
的第1行与第2行得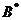 .
.
(C) 交换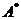 的第1列与第2列得
的第1列与第2列得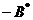 . (D) 交换
. (D) 交换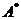 的第1行与第2行得
的第1行与第2行得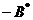 .
.
[ ]
三 、解答题(本题共9小题,满分94分.解答应写出文字说明、证明过程或演算步骤.)
(15)(本题满分11分)设函数f(x)连续,且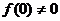 ,求极限
,求极限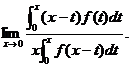
(16)(本题满分11分)如图,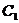 和
和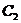 分别是
分别是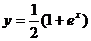 和
和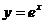 的图象,过点(0,1)的曲线
的图象,过点(0,1)的曲线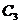 是一单调增函数的图象. 过
是一单调增函数的图象. 过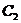 上任一点M(x,y)分别作垂直于x轴和y轴的直线
上任一点M(x,y)分别作垂直于x轴和y轴的直线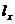 和
和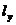 . 记
. 记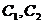 与
与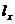 所围图形的面积为
所围图形的面积为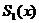 ;
;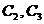 与
与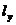 所围图形的面积为
所围图形的面积为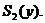 如果总有
如果总有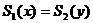 ,求曲线
,求曲线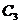 的方程
的方程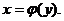
(17)(本题满分11分)如图,曲线C的方程为y=f(x),点(3,2)是它的一个拐点,直线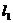 与
与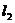 分别是曲线C在点(0,0)与(3,2)处的切线,其交点为(2,4). 设函数f(x)具有三阶连续导数,计算定积分
分别是曲线C在点(0,0)与(3,2)处的切线,其交点为(2,4). 设函数f(x)具有三阶连续导数,计算定积分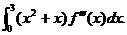
(18)(本题满分12分)用变量代换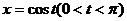 化简微分方程
化简微分方程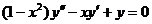 ,并求其满足
,并求其满足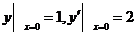 的特解.
的特解.
(19)(本题满分12分)
已知函数f(x)在[0,1]上连续,在(0,1)内可导,且f(0)=0,f(1)=1. 证明:
(I)存在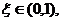 使得
使得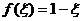 ;
;
(II)存在两个不同的点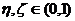 ,使得
,使得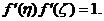
(20)(本题满分10分)
已知函数z=f(x,y) 的全微分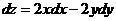 ,并且f(1,1,)=2. 求f(x,y)在椭圆域
,并且f(1,1,)=2. 求f(x,y)在椭圆域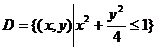 上的最大值和最小值.
上的最大值和最小值.
(21)(本题满分9分)
计算二重积分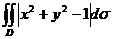 ,其中
,其中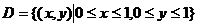 .
.
(22)(本题满分9分)
确定常数a,使向量组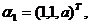
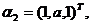
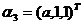 可由向量组
可由向量组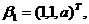
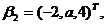
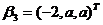 线性表示,但向量组
线性表示,但向量组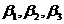 不能由向量组
不能由向量组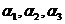 线性表示.
线性表示.
(23)(本题满分9分)
已知3阶矩阵A的第一行是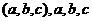 不全为零,矩阵
不全为零,矩阵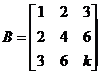 (k为常数),且AB=O, 求线性方程组Ax=0的通解.
(k为常数),且AB=O, 求线性方程组Ax=0的通解.
1..【分析】 本题属基本题型,幂指函数的求导(或微分)问题可化为指数函数求导或取对数后转化为隐函数求导.
【详解】 方法一: 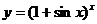 =
=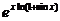 ,于是
,于是
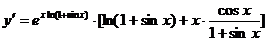 ,
,
从而 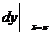 =
=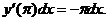
方法二: 两边取对数,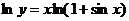 ,对x求导,得
,对x求导,得
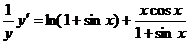 ,
,
于是 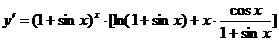 ,故
,故
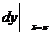 =
=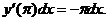
【评注】 幂指函数的求导问题,既不能单纯作为指数函数对待,也不能单纯作为幂函数,而直接运用相应的求导公式.
完全类似例题见《数学复习指南》(理工类)P.55【例2.15】
2..【分析】 本题属基本题型,直接用斜渐近线方程公式进行计算即可.
【详解】 因为a=
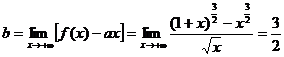 ,
,
于是所求斜渐近线方程为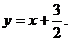
【评注】 如何求垂直渐近线、水平渐近线和斜渐近线,是基本要求,应熟练掌握。这里应注意两点:1)当存在水平渐近线时,不需要再求斜渐近线;2)若当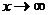 时,极限
时,极限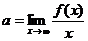 不存在,则应进一步讨论
不存在,则应进一步讨论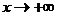 或
或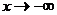 的情形,即在右或左侧是否存在斜渐近线,本题定义域为x>0,所以只考虑
的情形,即在右或左侧是否存在斜渐近线,本题定义域为x>0,所以只考虑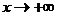 的情形.
的情形.
完全类似例题见《数学复习指南》(理工类)P.192【例7.32】
3..【分析】 作三角代换求积分即可.
【详解】 令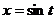 ,则
,则
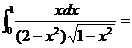
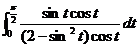
=
【评注】 本题为广义积分,但仍可以与普通积分一样对待作变量代换等.
完全类似例题见《数学复习指南》(理工类)P.130【例4.54】
4...
【分析】直接套用一阶线性微分方程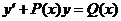 的通解公式:
的通解公式:
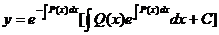 ,
,
再由初始条件确定任意常数即可.
【详解】 原方程等价为
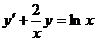 ,
,
于是通解为 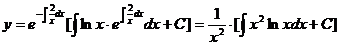
=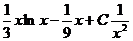 ,
,
由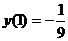 得C=0,故所求解为
得C=0,故所求解为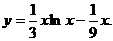
【评注】 本题虽属基本题型,但在用相关公式时应注意先化为标准型. 另外,本题也可如下求解:原方程可化为
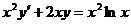 ,即
,即 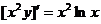 ,两边积分得
,两边积分得
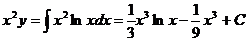 ,
,
再代入初始条件即可得所求解为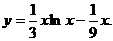
完全类似公式见《数学复习指南》(理工类)P.154
5…【分析】 题设相当于已知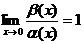 ,由此确定k即可.
,由此确定k即可.
【详解】 由题设,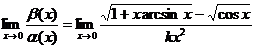
=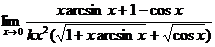
=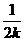
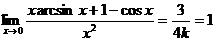 ,得
,得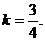
【评注】 无穷小量比较问题是历年考查较多的部分,本质上,这类问题均转化为极限的计算.
完全类似例题见《数学复习指南》(理工类)P.38【例1.62~63】
6…【分析】 将B写成用A右乘另一矩阵的形式,再用方阵相乘的行列式性质进行计算即可.
【详解】 由题设,有
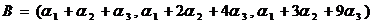
=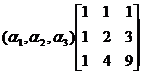 ,
,
于是有 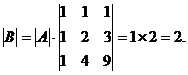
【评注】 本题相当于矩阵B的列向量组可由矩阵A的列向量组线性表示,关键是将其转化为用矩阵乘积形式表示。一般地,若
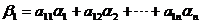 ,
,
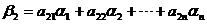 ,
,
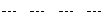
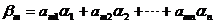 ,
,
则有 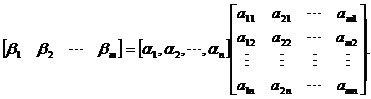
完全类似例题见《数学复习指南》(理工类)P.356【例1.5】
7….【分析】 先求出f(x)的表达式,再讨论其可导情形.
【详解】 当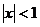 时,
时,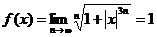 ;
;
当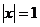 时,
时,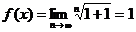 ;
;
当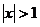 时,
时,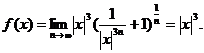
即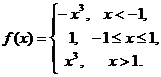 可见f(x)仅在x=
可见f(x)仅在x=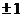 时不可导,故应选(C).
时不可导,故应选(C).
【评注】 本题综合考查了数列极限和导数概念两个知识点.
完全类似例题见《数学复习指南》(理工类)P.56【例2.20】
8….
【分析】 本题可直接推证,但最简便的方法还是通过反例