|
微信搜索关注"91考试网"公众号,领30元,获取公务员、事业编、教师等考试资料40G!
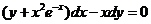 的通解是 . 的通解是 .
【答案】 应填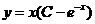 . .
(11)曲线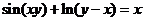 在点 在点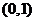 的切线方程为 . 的切线方程为 .
【答案】 应填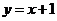 . .
【详解】
(12)曲线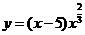 的拐点坐标为 . 的拐点坐标为 .
【答案】 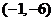 . .
【详解】
(13)设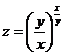 ,则 ,则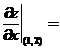 . .
【答案】 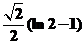 . .
(14)设3阶矩阵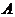 的特征值为 的特征值为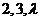 .若行列式 .若行列式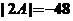 ,则 ,则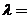 ___________. ___________.
【答案】应填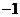 . .
三、解答题(15-23小题,共94分).
(15)(本题满分9分)
求极限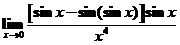 . .
【详解1】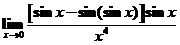 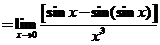
=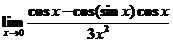 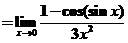
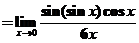 (或 (或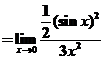 ,或 ,或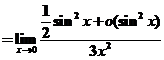 ) )
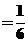 . .
【详解2】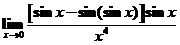 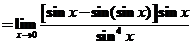
=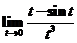 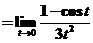 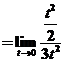 (或 (或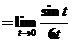 ) )
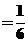 . .
(16)(本题满分10分)
设函数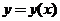 由参数方程 由参数方程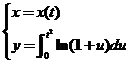 确定,其中 确定,其中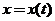 是初值问题 是初值问题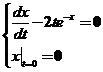 的解,求 的解,求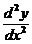 . .
【详解1】由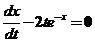 得 得
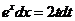 ,积分得 ,积分得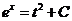 . .
由条件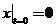 ,得 ,得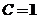 ,即 ,即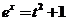 , ,
故 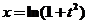 . .
方程组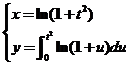 两端同时对 两端同时对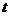 求导得 求导得
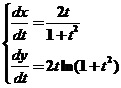 . .
所以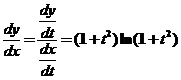 , ,
从而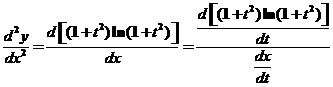
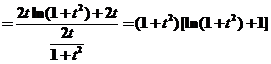 . .
17(本题满分9分)计算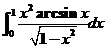 . .
【详解1】 由于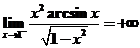 ,故 ,故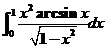 是反常积分. 是反常积分.
令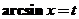 ,有 ,有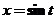 , ,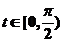 . .
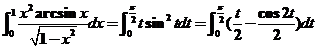
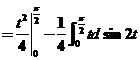 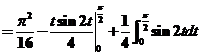
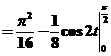 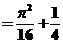 . .
【详解2】 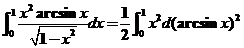
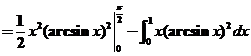
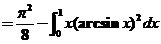
令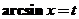 ,有 ,有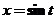 , ,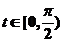 . .
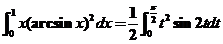
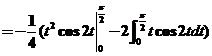
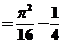 , ,
所以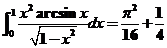 . .
(18)(本题满分11分)
计算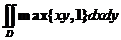 ,其中 ,其中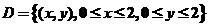 . .
【详解】将区域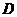 分成如图所示得两个子区域 分成如图所示得两个子区域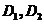 和 和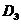 .于是 .于是
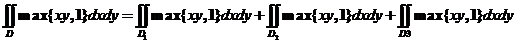
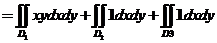 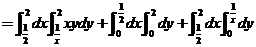
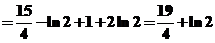 . .
(19)(本题满分11分)
设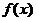 是区间 是区间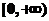 上具有连续导数的单调增加函数,且 上具有连续导数的单调增加函数,且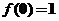 .对任意的 .对任意的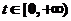 ,直线 ,直线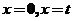 ,曲线 ,曲线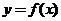 以及 以及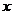 轴所围成的曲边梯形绕 轴所围成的曲边梯形绕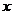 轴旋转一周生成一旋转体,若该旋转体的侧面面积在数值上等于其体积的2倍,求函数 轴旋转一周生成一旋转体,若该旋转体的侧面面积在数值上等于其体积的2倍,求函数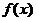 的表达式. 的表达式.
【详解】根据题意,因为
旋转体体积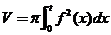 ,侧面积 ,侧面积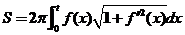 . .
所以 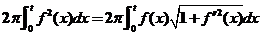 . .
上式两边同时对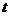 求导得 求导得
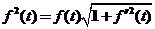 . .
解得 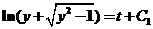 , ,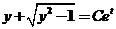 . .
由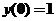 ,得 ,得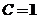 . .
所以 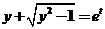 或 或 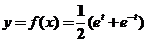 . .
(20)(本题满分11分)
(I) 证明积分中值定理:若函数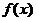 在闭区间 在闭区间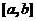 上连续,则至少存在一点 上连续,则至少存在一点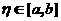 ,使得 ,使得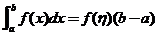 ; ;
(II) 若函数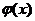 具有二阶导数,且满足 具有二阶导数,且满足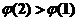 , ,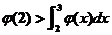 ,则至少存在一点 ,则至少存在一点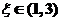 ,使得 ,使得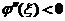 . .
【证法1】若函数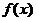 在闭区间 在闭区间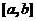 上连续,则必存在最大值 上连续,则必存在最大值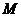 和最小值 和最小值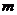 .即 .即
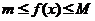 , ,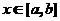
于是有
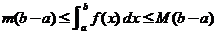 . .
即
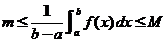
根据闭区间上连续函数的介值定理,在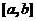 上至少存在一点 上至少存在一点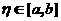 ,使得 ,使得
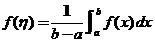
因此而的证.
(II)存在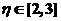 ,使得 ,使得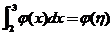 . .
由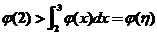 ,知 ,知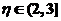 . .
由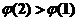 ,利用微分中值定理,存在 ,利用微分中值定理,存在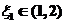 ,使得 ,使得
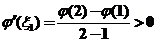 . .
由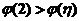 ,利用微分中值定理,存在 ,利用微分中值定理,存在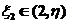 ,使得 ,使得
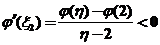 . .
存在存在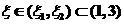 ,使得 ,使得
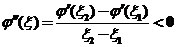 . .
(21)(本题满分11分)
求函数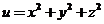 在约束条件 在约束条件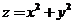 和 和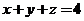 下的最大值和最小值. 下的最大值和最小值.
【详解1】作拉格朗日函数
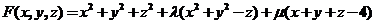 . .
令
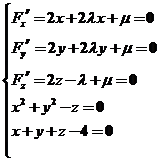
解之得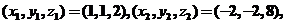 故所求得最大值为72,最小值为6. 故所求得最大值为72,最小值为6.
【详解2】由题意知,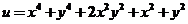 在条件 在条件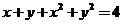 下的最值. 下的最值.
令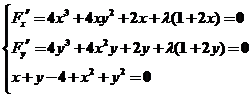
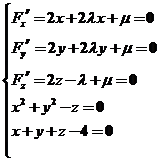
解之得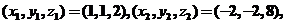 故所求得最大值为72,最小值为6. 故所求得最大值为72,最小值为6.
(22) (本题满分12分).
设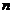 元线性方程组 元线性方程组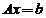 ,其中 ,其中
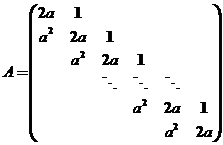 , ,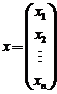 , ,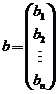 . .
(I)证明行列式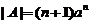 ; ;
(II)当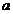 为何值时,该方程组有惟一解,并求 为何值时,该方程组有惟一解,并求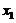 . .
(III)当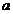 为何值时,该方程组有无穷多解,并求其通解. 为何值时,该方程组有无穷多解,并求其通解.
【详解】(I)【证法1】数学归纳法.记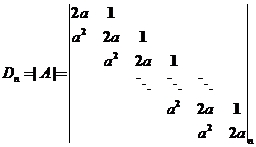
以下用数学归纳法证明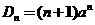 . .
当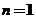 时, 时,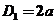 ,结论成立. ,结论成立.
当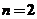 时, 时,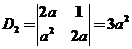 ,结论成立. ,结论成立.
假设结论对小于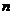 的情况成立.将 的情况成立.将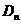 按第一行展开得 按第一行展开得
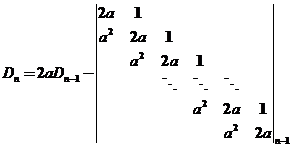
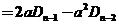
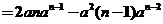
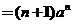
故 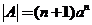 . .
【注】本题(1)也可用递推法.由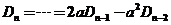 得, 得,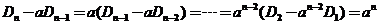 .于是 .于是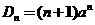
(I)【证法2】消元法.记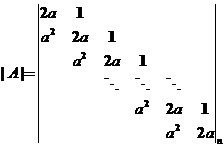
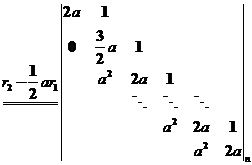
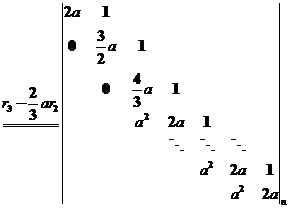
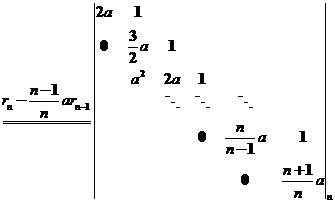
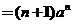 . .
(II)【详解】当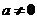 时,方程组系数行列式 时,方程组系数行列式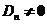 ,故方程组有惟一解.由克莱姆法则,将 ,故方程组有惟一解.由克莱姆法则,将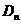 得第一列换成 得第一列换成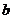 ,得行列式为 ,得行列式为
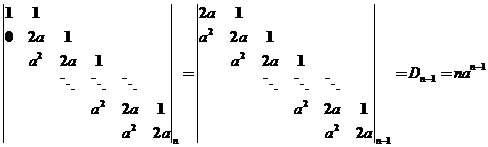
所以,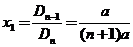 . .
(III)【详解】 当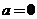 时,方程组为 时,方程组为
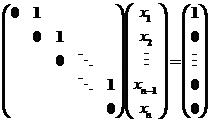
此时方程组系数矩阵得秩和增广矩阵得秩均为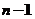 ,所以方程组有无穷多组解,其通解为 ,所以方程组有无穷多组解,其通解为
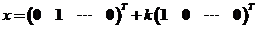 ,其中 ,其中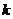 为任意常数. 为任意常数.
(23) (本题满分10分)
设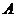 为3阶矩阵, 为3阶矩阵,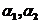 为 为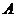 的分别属于特征值 的分别属于特征值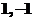 的特征向量,向量 的特征向量,向量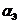 满足 满足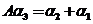 , ,
(I)证明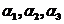 线性无关; 线性无关;
(II)令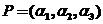 ,求 ,求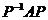 . .
【详解】(I)【证明】设有一组数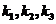 ,使得 ,使得 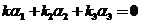 . .
用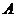 左乘上式,得 左乘上式,得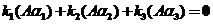 . .
因为 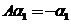 , , 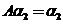 , ,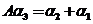 , ,
所以 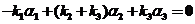 , ,
即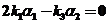 . .
由于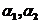 是属于不同特征值得特征向量,所以线性无关,因此 是属于不同特征值得特征向量,所以线性无关,因此
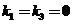 ,从而有 ,从而有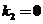 . .
故 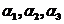 线性无关. 线性无关.
(II)由题意,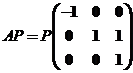 .而由(I)知, .而由(I)知,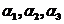 线性无关,从而 线性无关,从而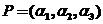 可逆.故 可逆.故
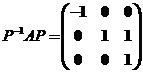 . .
|