微信搜索关注"91考试网"公众号,领30元,获取公务员、事业编、教师等考试资料40G!
2007年考研数学二真题附答案详解
一、选择题:1~10小题,每小题4分,共40分. 在每小题给出的四个选项中,只有一项符合题目要求,把所选项前的字母填在题后的括号内.
(1)当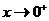 时,与
时,与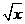 等价的无穷小量是
等价的无穷小量是
(A)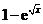 (B)
(B)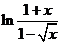 (C)
(C)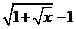 (D)
(D)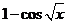 [ ]
[ ]
(2)函数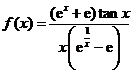 在
在 上的第一类间断点是
上的第一类间断点是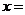 ( )
( )
(A)0 (B)1 (C)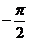 (D)
(D)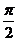
(3)如图,连续函数 在区间
在区间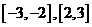 上的图形分别是直径为1的上、下半圆周,在区间
上的图形分别是直径为1的上、下半圆周,在区间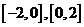 的图形分别是直径为2的下、上半圆周,设
的图形分别是直径为2的下、上半圆周,设 ,则下列结论正确的是:
,则下列结论正确的是:
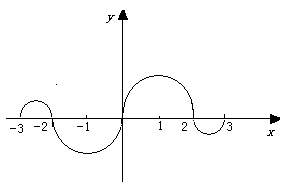
(A)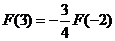 (B)
(B) 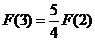
(C)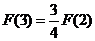 (D)
(D)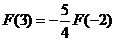 [ ]
[ ]
(4)设函数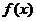 在
在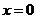 处连续,下列命题错误的是:
处连续,下列命题错误的是:
(A)若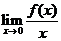 存在,则
存在,则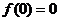 (B)若
(B)若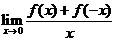 存在,则
存在,则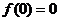 .
.
(B)若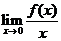 存在,则
存在,则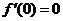 (D)若
(D)若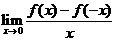 存在,则
存在,则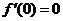 .
.
[ ]
(5)曲线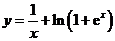 的渐近线的条数为
的渐近线的条数为
(A)0. (B)1. (C)2. (D)3. [ ]
(6)设函数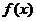 在
在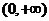 上具有二阶导数,且
上具有二阶导数,且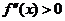 ,令
,令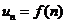 ,则下列结论正确的是:
,则下列结论正确的是:
(A) 若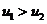 ,则
,则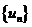 必收敛. (B) 若
必收敛. (B) 若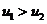 ,则
,则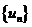 必发散
必发散
(C) 若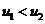 ,则
,则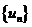 必收敛. (D) 若
必收敛. (D) 若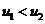 ,则
,则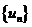 必发散. [ ]
必发散. [ ]
(7)二元函数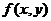 在点
在点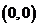 处可微的一个充要条件是
处可微的一个充要条件是
(A)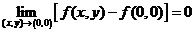 .
.
(B) .
.
(C)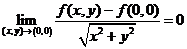 .
.
(D)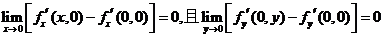 .
.
(8)设函数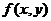 连续,则二次积分
连续,则二次积分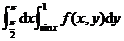 等于
等于
(A)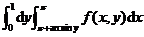 (B)
(B)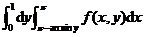
(C)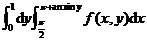 (D)
(D)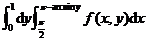
(9)设向量组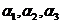 线性无关,则下列向量组线性相关的是
线性无关,则下列向量组线性相关的是
线性相关,则
(A) 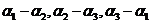 (B)
(B) 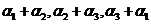
(C) 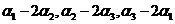 . (D)
. (D) 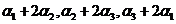 . [ ]
. [ ]
(10)设矩阵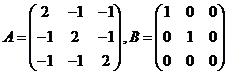 ,则
,则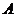 与
与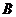
(A) 合同且相似 (B)合同,但不相似.
(C) 不合同,但相似. (D) 既不合同也不相似 [ ]
二、填空题:11~16小题,每小题4分,共24分. 把答案填在题中横线上.
(11) 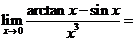 __________.
__________.
(12)曲线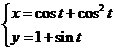 上对应于
上对应于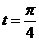 的点处的法线斜率为_________.
的点处的法线斜率为_________.
(13)设函数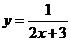 ,则
,则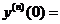 ________.
________.
(14) 二阶常系数非齐次微分方程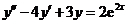 的通解为
的通解为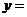 ________.
________.
(15) 设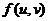 是二元可微函数,
是二元可微函数,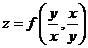 ,则
,则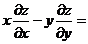 __________.
__________.
(16)设矩阵 ,则
,则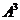 的秩为 .
的秩为 .
三、解答题:17~24小题,共86分. 解答应写出文字说明、证明过程或演算步骤.
(17) (本题满分10分)
设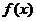 是区间
是区间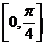 上单调、可导的函数,且满足
上单调、可导的函数,且满足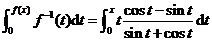 ,其中
,其中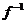 是
是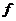 的反函数,求
的反函数,求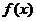 .
.
(18)(本题满分11分)
设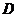 是位于曲线
是位于曲线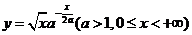 下方、
下方、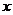 轴上方的无界区域.
轴上方的无界区域.
(Ⅰ)求区域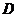 绕
绕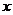 轴旋转一周所成旋转体的体积
轴旋转一周所成旋转体的体积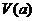 ;
;
(Ⅱ)当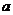 为何值时,
为何值时,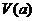 最小?并求此最小值.
最小?并求此最小值.
(19)(本题满分10分)求微分方程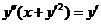 满足初始条件
满足初始条件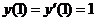 的特解
的特解
(20)(本题满分11分)已知函数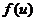 具有二阶导数,且
具有二阶导数,且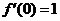 ,函数
,函数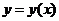 由方程
由方程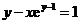 所确定,设
所确定,设 ,求
,求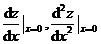 .
.
(21) (本题满分11分)
设函数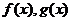 在
在 上连续,在
上连续,在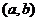 内具有二阶导数且存在相等的最大值,
内具有二阶导数且存在相等的最大值,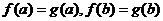 ,证明:存在
,证明:存在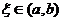 ,使得
,使得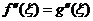 .
.
(22) (本题满分11分)
设二元函数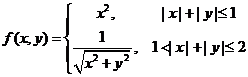 ,计算二重积分
,计算二重积分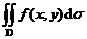 ,其中
,其中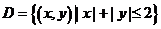 .
.
(23) (本题满分11分)
设线性方程组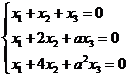 与方程
与方程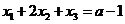 有公共解,求
有公共解,求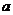 的值及所有公共解.
的值及所有公共解.
1….【分析】本题为等价无穷小的判定,利用定义或等价无穷小代换即可.
【详解】当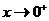 时,
时,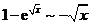 ,
,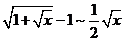 ,
,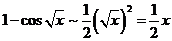 ,
,
故用排除法可得正确选项为(B).
事实上,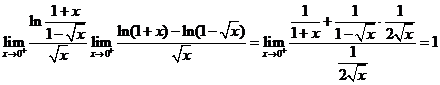 ,
,
或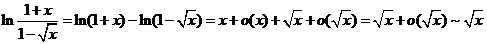 .
.
所以应选(B)
【评注】本题为关于无穷小量比较的基本题型,利用等价无穷小代换可简化计算.
2…【分析】因为函数为初等函数,则先找出函数的无定义点,再根据左右极限判断间断点的类型.
【详解】函数在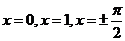 均无意义,
均无意义,
而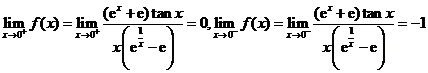 ;
;
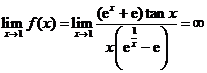 ;
;
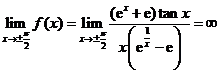 .
.
所以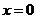 为函数
为函数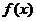 的第一类间断点,故应选(A).
的第一类间断点,故应选(A).
【评注】本题为基础题型. 对初等函数来讲,无定义点即为间断点,然后再根据左右极限判断间断点的类型;对分段函数来讲,每一分段支中的无定义点为间断点,而分段点也可能为间断点,然后求左右极限进行判断.
段函数的定积分.
【详解】利用定积分的几何意义,可得
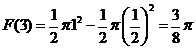 ,
,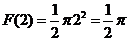 ,
,
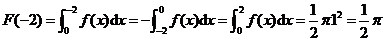 .
.
所以 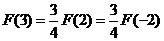 ,故选(C).
,故选(C).
【评注】本题属基本题型. 本题利用定积分的几何意义比较简便.
4……【分析】本题考查可导的极限定义及连续与可导的关系. 由于题设条件含有抽象函数,本题最简便的方法是用赋值法求解,即取符合题设条件的特殊函数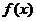 去进行判断,然后选择正确选项.
去进行判断,然后选择正确选项.
【详解】取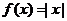 ,则
,则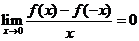 ,但
,但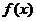 在
在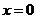 不可导,故选(D).
不可导,故选(D).
事实上,
在(A),(B)两项中,因为分母的极限为0,所以分子的极限也必须为0,则可推得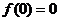 .
.
在(C)中,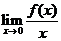 存在,则
存在,则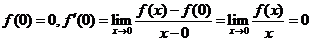 ,所以(C)项正确,故选(D)
,所以(C)项正确,故选(D)
【评注】对于题设条件含抽象函数或备选项为抽象函数形式结果以及数值型结果的选择题,用赋值法求解往往能收到奇效.
5……【分析】利用曲线的渐近线的求解公式求出水平渐近线,垂直渐近线和斜渐近线,然后判断.
【详解】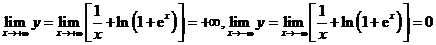 ,
,
所以 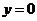 是曲线的水平渐近线;
是曲线的水平渐近线;