|
微信搜索关注"91考试网"公众号,领30元,获取公务员、事业编、教师等考试资料40G!
sp; .
(13) 曲线 上曲率为 上曲率为 的点的坐标是 . 的点的坐标是 .
(14) 设 为3阶矩阵, 为3阶矩阵, , , 为 为 伴随矩阵,若交换 伴随矩阵,若交换 的第1行与第2行得矩阵 的第1行与第2行得矩阵 ,则 ,则 . .
三、解答题:15-23小题,共94分.请将解答写在答题纸指定位置上.解答应写出文字说明、证明过程或演算步骤.
(15)(本题满分 10 分)
已知函数 ,记 ,记 , ,
(I)求 的值; 的值;
(II)若 时, 时, 与 与 是同阶无穷小,求常数 是同阶无穷小,求常数 的值. 的值.
(16)(本题满分 10 分)
求函数 的极值. 的极值.
(17)(本题满分12分)
过 点作曲线 点作曲线 的切线,切点为 的切线,切点为 ,又 ,又 与 与 轴交于 轴交于 点,区域 点,区域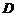 由 由 与直线 与直线 围成,求区域 围成,求区域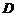 的面积及 的面积及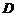 绕 绕 轴旋转一周所得旋转体的体积. 轴旋转一周所得旋转体的体积.
(18)(本题满分 10 分)
计算二重积分 ,其中区域 ,其中区域 为曲线 为曲线 与极轴围成. 与极轴围成.
(19)(本题满分10分)
已知函数 满足方程 满足方程 及 及 , ,
(I) 求 的表达式; 的表达式;
(II) 求曲线 的拐点. 的拐点.
(20)(本题满分10分)
证明 , , . .
(21)(本题满分10 分)
(I)证明方程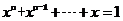  ,在区间 ,在区间 内有且仅有一个实根; 内有且仅有一个实根;
(II)记(I)中的实根为 ,证明 ,证明 存在,并求此极限. 存在,并求此极限.
(22)(本题满分11 分)
设 , ,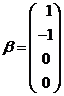
(I) 计算行列式 ; ;
(II) 当实数 为何值时,方程组 为何值时,方程组 有无穷多解,并求其通解. 有无穷多解,并求其通解.
(23)(本题满分11 分)
已知 ,二次型 ,二次型 的秩为2, 的秩为2,
(I) 求实数 的值; 的值;
(II) 求正交变换 将 将 化为标准形. 化为标准形.











。
|