微信搜索关注"91考试网"公众号,领30元,获取公务员、事业编、教师等考试资料40G!
2013年考研数学(二)真题附答案详解
一、选择题:1~8小题,每小题4分,共32分,下列每小题给出的四个选项中,只有一项符合题目要求的,请将所选项前的字母填在答题纸指定位置上.
(1)设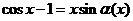 ,其中
,其中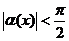 ,则当
,则当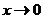 时,
时,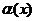 是( )
是( )
(A)比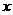 高阶的无穷小 (B)比
高阶的无穷小 (B)比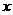 低阶的无穷小
低阶的无穷小
(C)与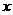 同阶但不等价的无穷小 (D)与
同阶但不等价的无穷小 (D)与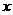 等价的无穷小
等价的无穷小
(2)设函数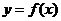 由方程
由方程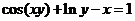 确定,则
确定,则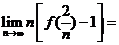 ( )
( )
(A)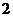 (B)
(B)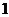 (C)
(C)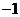 (D)
(D)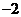
(3)设函数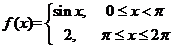 ,
,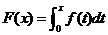 ,则( )
,则( )
(A)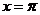 是函数
是函数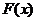 的跳跃间断点 (B)
的跳跃间断点 (B)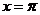 是函数
是函数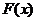 的可去间断点
的可去间断点
(C)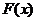 在
在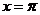 处连续但不可导 (D)
处连续但不可导 (D)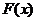 在
在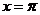 处可导
处可导
(4)设函数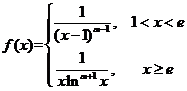 ,若反常积分
,若反常积分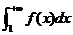 收敛,则( )
收敛,则( )
(A)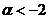 (B)
(B)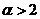 (C)
(C)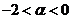 (D)
(D)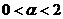
(5)设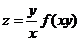 ,其中函数
,其中函数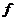 可微,则
可微,则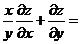 ( )
( )
(A)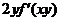 (B)
(B)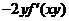 (C)
(C)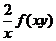 (D)
(D)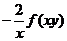
(6)设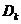 是圆域
是圆域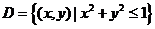 在第
在第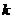 象限的部分,记
象限的部分,记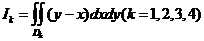 ,则( )
,则( )
(A)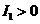 (B)
(B)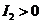 (C)
(C)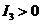 (D)
(D)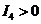
(7)设矩阵A,B,C均为n阶矩阵,若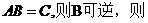
(A)矩阵C的行向量组与矩阵A的行向量组等价
(B)矩阵C的列向量组与矩阵A的列向量组等价
(C)矩阵C的行向量组与矩阵B的行向量组等价
(D)矩阵C的行向量组与矩阵B的列向量组等价
(8)矩阵 与
与 相似的充分必要条件为
相似的充分必要条件为
(A)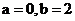
(B)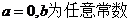
(C)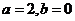
(D)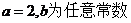
二、填空题:9-14小题,每小题4分,共24分,请将答案写在答题纸指定位置上.
(9) 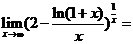 .
.
(10) 设函数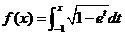 ,则
,则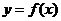 的反函数
的反函数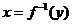 在
在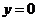 处的导数
处的导数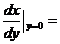 .
.
(11)设封闭曲线L的极坐标方程为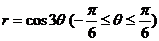 ,则L所围成的平面图形的面积为 .
,则L所围成的平面图形的面积为 .
(12)曲线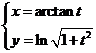 上对应于
上对应于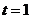 的点处的法线方程为 .
的点处的法线方程为 .
(13)已知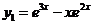 ,
,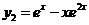 ,
,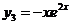 是某二阶常系数非齐次线性微分方程的3个解,该方程满足条件
是某二阶常系数非齐次线性微分方程的3个解,该方程满足条件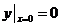
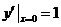 的解为
的解为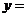 .
.
(14)设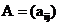 是三阶非零矩阵,
是三阶非零矩阵,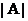 为A的行列式,
为A的行列式,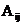 为
为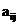 的代数余子式,若
的代数余子式,若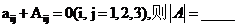
三、解答题:15—23小题,共94分.请将解答写在答题纸指定位置上.解答应写出文字说明、证明过程或演算步骤.
(15)(本题满分10分)
当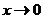 时,
时,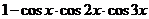 与
与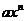 为等价无穷小,求
为等价无穷小,求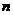 与
与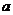 的值。
的值。
(16)(本题满分10分)
设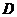 是由曲线
是由曲线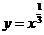 ,直线
,直线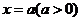 及
及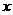 轴所围成的平面图形,
轴所围成的平面图形,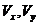 分别是
分别是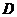 绕
绕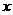 轴,
轴,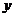 轴旋转一周所得旋转体的体积,若
轴旋转一周所得旋转体的体积,若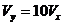 ,求
,求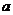 的值。
的值。
(17)(本题满分10分)
设平面内区域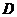 由直线
由直线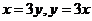 及
及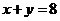 围成.计算
围成.计算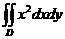 。
。
(18)(本题满分10分)
设奇函数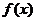 在
在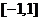 上具有二阶导数,且
上具有二阶导数,且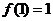 .证明:
.证明:
(I)存在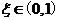 ,使得
,使得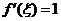 ;(II)存在
;(II)存在 ,使得
,使得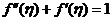 。
。
(19)(本题满分11分)
求曲线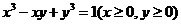 上的点到坐标原点的最长距离与最短距离。
上的点到坐标原点的最长距离与最短距离。
(20)(本题满分11分)
设函数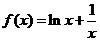 ,
,
(I)求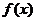 的最小值
的最小值
(II)设数列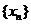 满足
满足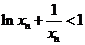 ,证明
,证明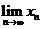 存在,并求此极限.
存在,并求此极限.
(21)(本题满分11分)
设曲线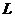 的方程为
的方程为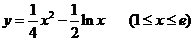 ,
,
(1)求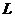 的弧长;
的弧长;
(2)设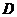 是由曲线
是由曲线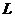 ,直线
,直线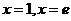 及
及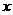 轴所围平面图形,求
轴所围平面图形,求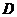 的形心的横坐标。
的形心的横坐标。
(22)(本题满分11分)
设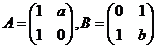 ,当
,当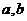 为何值时,存在矩阵
为何值时,存在矩阵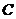 使得
使得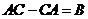 ,并求所有矩阵
,并求所有矩阵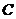 。
。
(23)(本题满分11分)
设二次型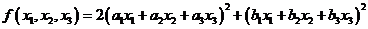 ,记
,记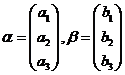 。
。
(I)证明二次型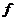 对应的矩阵为
对应的矩阵为 ;
;
(II)若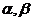 正交且均为单位向量,证明二次型
正交且均为单位向量,证明二次型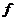 在正交变化下的标准形为二次型
在正交变化下的标准形为二次型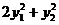 。
。
2013年全国硕士研究生入学统一考试
数学二试题答案
一、选择题:1~8小题,每小题4分,共32分,下列每小题给出的四个选项中,只有一项符合题目要求的,请将所选项前的字母填在答题纸指定位置上.
(1)设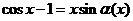 ,其中
,其中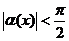 ,则当
,则当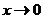 时,
时,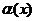 是( )
是( )
(A)比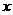 高阶的无穷小 (B)比
高阶的无穷小 (B)比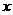 低阶的无穷小
低阶的无穷小
(C)与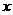 同阶但不等价的无穷小 (D)与
同阶但不等价的无穷小 (D)与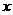 等价的无穷小
等价的无穷小
【答案】(C)
【解析】因为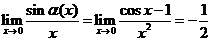 ,所以
,所以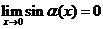 ,
,
因此当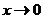 时,
时,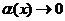 ,所以
,所以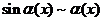 ,所以
,所以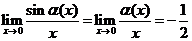 ,
,
所以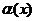 是与
是与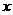 同阶但不等价的无穷小。
同阶但不等价的无穷小。
(2)设函数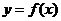 由方程
由方程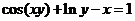 确定,则
确定,则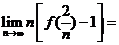 ( )
( )
(A)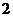 (B)
(B)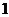 (C)
(C)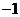 (D)
(D)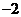
【答案】(A)
【解析】由于 ,所以
,所以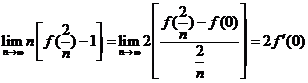 ,
,
对此隐函数两边求导得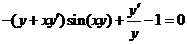 ,所以
,所以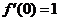 ,故
,故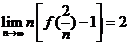 。
。
(3)设函数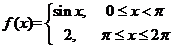 ,
,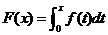 ,则( )
,则( )
(A)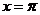 是函数
是函数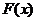 的跳跃间断点 (B)
的跳跃间断点 (B)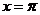 是函数
是函数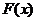 的可去间断点
的可去间断点
(C)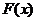 在
在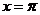 处连续但不可导 (D)
处连续但不可导 (D)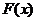 在
在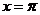 处可导
处可导
【答案】(C)
【解析】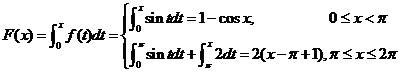 ,
,
由于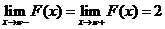 ,所以
,所以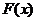 在
在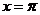 处连续;
处连续;
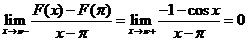 ,
,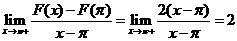 ,
,
所以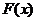 在
在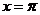 处不可导。
处不可导。
(4)设函数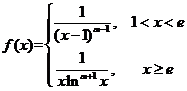 ,若反常积分
,若反常积分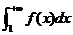 收敛,则( )
收敛,则( )
(A)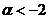 (B)
(B)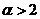 (C)
(C)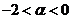 (D)
(D)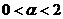
【答案】(D)
【解析】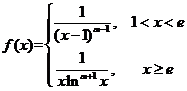
因为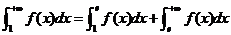 ,
,
当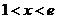 时,
时,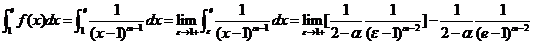 ,
,
要使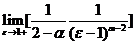 存在,需满足
存在,需满足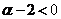 ;
;
当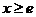 时,
时,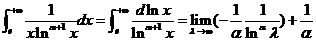 ,
,
要使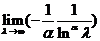 存在,需满足
存在,需满足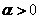 ;所以
;所以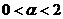 。
。
(5)设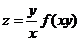 ,其中函数
,其中函数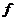 可微,则
可微,则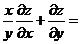 ( )
( )
(A)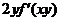 (B)
(B)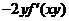 (C)
(C)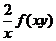 (D)
(D)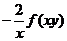
【答案】(A)
【解析】已知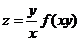 ,所以
,所以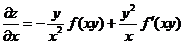 ,
,
所以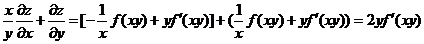 。
。
(6)设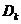 是圆域
是圆域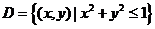 在第
在第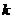 象限的部分,记
象限的部分,记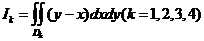 ,则( )
,则( )
(A)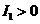 (B)
(B)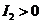 (C)
(C)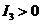 (D)
(D)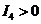
【答案】(B)
【解析】令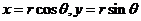 ,则有
,则有
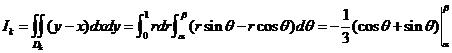
故当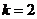 时,
时,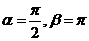 ,此时有
,此时有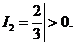 故正确答案选B。
故正确答案选B。
(7)设矩阵A,B,C均为n阶矩阵,若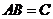 ,且
,且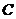 可逆,则( )
可逆,则( )
(A)矩阵C的行向量组与矩阵A的行向量组等价
(B)矩阵C的列向量组与矩阵A的列向量组等价
(C)矩阵C的行向量组与矩阵B的行向量组等价
(D)矩阵C的行向量组与矩阵B的列向量组等价
【答案】(B)
【解析】由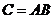 可知C的列向量组可以由A的列向量组线性表示,又B可逆,故有
可知C的列向量组可以由A的列向量组线性表示,又B可逆,故有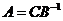 ,从而A的列向量组也可以由C的列向量组线性表示,故根据向量组等价的定义可知正确选项为(B)。
,从而A的列向量组也可以由C的列向量组线性表示,故根据向量组等价的定义可知正确选项为(B)。
(8)矩阵 与
与 相似的充分必要条件为
相似的充分必要条件为
(A)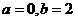
(B)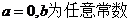
(C)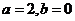
(D)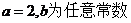
【答案】(B)
【解析】由于 为实对称矩阵,故一定可以相似对角化,从而
为实对称矩阵,故一定可以相似对角化,从而 与
与 相似的充分必要条件为
相似的充分必要条件为 的特征值为
的特征值为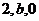 。
。
又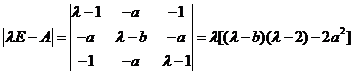 ,从而
,从而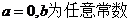 。
。
二、填空题:9-14小题,每小题4分,共24分,请将答案写在答题纸指定位置上.
(9) 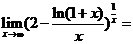 .
.
【答案】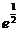
【解析】原式=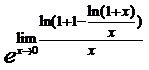 ,
,
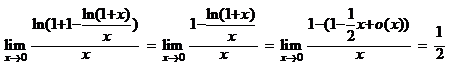
因此答案为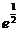 .
.
(10) 设函数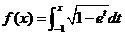 ,则
,则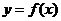 的反函数
的反函数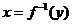 在
在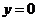 处的导数
处的导数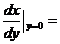 .
.
【答案】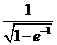
【解析】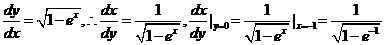
(11)设封闭曲线L的极坐标方程为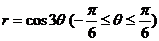 ,则L所围成的平面图形的面积为 .
,则L所围成的平面图形的面积为 .
【答案】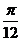
【解析】所围图形的面积是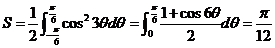
(12)曲线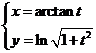 上对应于
上对应于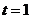 的点处的法线方程为 .
的点处的法线方程为 .
【答案】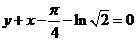
【解析】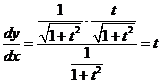 ,
,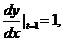
当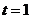 时,
时,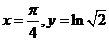 ,故法线方程为
,故法线方程为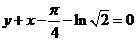 .
.
(13)已知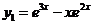 ,
,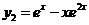 ,
,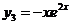 是某二阶常系数非齐次线性微分方程的3个解,该方程满足条件
是某二阶常系数非齐次线性微分方程的3个解,该方程满足条件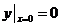
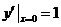 的解为
的解为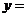 .
.
【答案】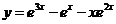
【解析】由题意知: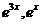 是对应齐次方程的解,
是对应齐次方程的解,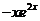 是非齐次方程的解,
是非齐次方程的解,
故非齐次的通解为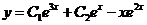 ,将初始条件代入,得到
,将初始条件代入,得到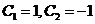 ,
,
故满足条件的解为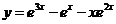 。
。
(14)设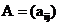 是三阶非零矩阵,
是三阶非零矩阵,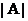 为A的行列式,
为A的行列式,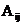 为
为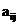 的代数余子式,若
的代数余子式,若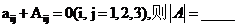
【答案】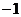
【解析】
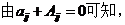
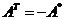
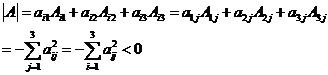
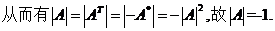
三、解答题:15—23小题,共94分.请将解答写在答题纸指定位置上.解答应写出文字说明、证明过程或演算步骤.
(15)(本题满分10分)
当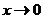 时,
时,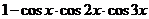 与
与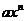 为等价无穷小,求
为等价无穷小,求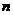 与
与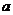 的值。
的值。
【解析】因为当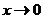 时,
时,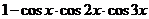 与
与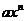 为等价无穷小
为等价无穷小
所以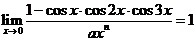
又因为:
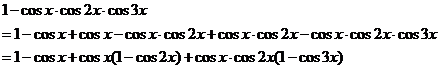
即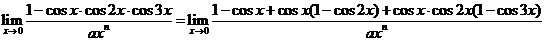
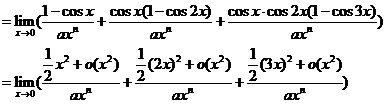
所以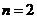 且
且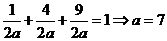
(16)(本题满分10分)
设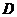 是由曲线
是由曲线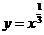 ,直线
,直线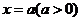 及
及 轴所围成的平面
轴所围成的平面