微信搜索关注"91考试网"公众号,领30元,获取公务员、事业编、教师等考试资料40G!
程解的结构:设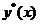 是二阶线性非齐次方程
是二阶线性非齐次方程
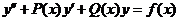 的一个特解.
的一个特解.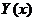 是与之对应的齐次方程
是与之对应的齐次方程
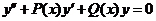 的通解,则
的通解,则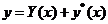 是非齐次方程的通解.
是非齐次方程的通解.
2. 二阶常系数线性齐次方程通解的求解方法:对于求解二阶常系数线性齐次方程的通解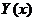 ,可用特征方程法求解:即
,可用特征方程法求解:即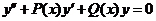 中的
中的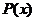 、
、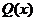 均是常数,方程变为
均是常数,方程变为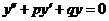 .其特征方程写为
.其特征方程写为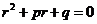 ,在复数域内解出两个特征根
,在复数域内解出两个特征根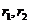 ;
;
分三种情况:
(1) 两个不相等的实数根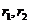 ,则通解为
,则通解为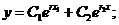
(2) 两个相等的实数根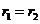 ,则通解为
,则通解为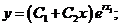
(3) 一对共轭复根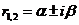 ,则通解为
,则通解为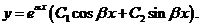 其中
其中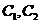 为常数.
为常数.
3.对于求解二阶线性非齐次方程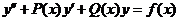 的一个特解
的一个特解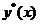 ,可用待定系数法,有结论如下:
,可用待定系数法,有结论如下:
如果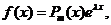 则二阶常系数线性非齐次方程具有形如
则二阶常系数线性非齐次方程具有形如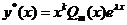
的特解,其中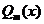 是与
是与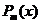 相同次数的多项式,而
相同次数的多项式,而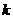 按
按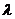 不是特征方程的根、是特征方程的单根或是特征方程的重根依次取0、1或2.
不是特征方程的根、是特征方程的单根或是特征方程的重根依次取0、1或2.
如果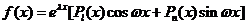 ,则二阶常系数非齐次线性微分方程
,则二阶常系数非齐次线性微分方程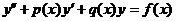 的特解可设为
的特解可设为
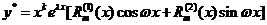 ,
,
其中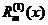 与
与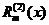 是
是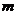 次多项式,
次多项式,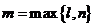 ,而
,而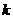 按
按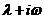 (或
(或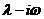 )不是特征方程的根、或是特征方程的单根依次取为
)不是特征方程的根、或是特征方程的单根依次取为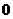 或
或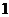 .
.
五、(本题满分8分)
【解析】将原式表成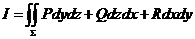 ,则
,则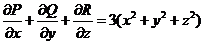 .
.
以考虑用高斯公式来求解,但曲面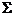 不是封闭的,要添加辅助面.如果本题采用投影法计算是比较复杂的,故不采用.
不是封闭的,要添加辅助面.如果本题采用投影法计算是比较复杂的,故不采用.
添加辅助面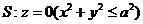 ,法向量朝下,
,法向量朝下,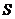 与
与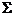 围成区域
围成区域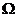 ,
,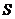 与
与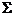 取
取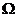 的外法向量.在
的外法向量.在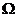 上用高斯公式得
上用高斯公式得
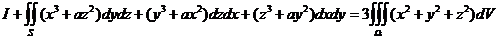 .
.
用球坐标变换求右端的三重积分得
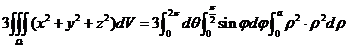
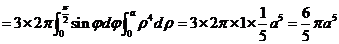 .
.
注意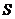 垂直于平面
垂直于平面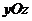 与平面
与平面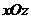 ,将积分投影到
,将积分投影到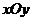 平面上,所以左端
平面上,所以左端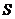 上的曲面积分为
上的曲面积分为 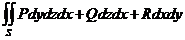
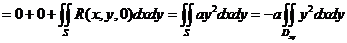
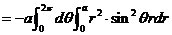 (极坐标变换)
(极坐标变换)
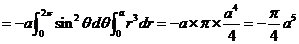 .
.
因此 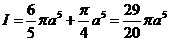 .
.
【相关知识点】1.高斯公式:设空间闭区域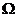 是由分片光滑的闭曲面
是由分片光滑的闭曲面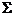 所围成,函数
所围成,函数
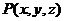 、
、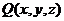 、
、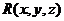 在
在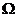 上具有一阶连续偏导数,则有
上具有一阶连续偏导数,则有
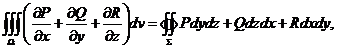
或 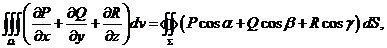
这里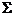 是
是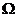 的整个边界曲面的外侧,
的整个边界曲面的外侧,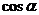 、
、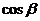 、
、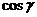 是
是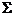 在点
在点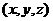 处的法向量的方向余弦.上述两个公式叫做高斯公式.
处的法向量的方向余弦.上述两个公式叫做高斯公式.
2.对于球面坐标与直角坐标的关系为:
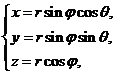
其中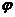 为向量与
为向量与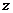 轴正向的夹角,
轴正向的夹角,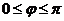 ;
;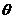 为从正
为从正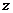 轴来看自
轴来看自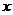 轴按逆时针方向转到向量在
轴按逆时针方向转到向量在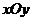 平面上投影线段的角,
平面上投影线段的角,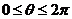 ;
; 为向量的模长,
为向量的模长,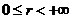 .
.
球面坐标系中的体积元素为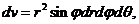 则三重积分的变量从直角坐标变换为球面坐标的公式是:
则三重积分的变量从直角坐标变换为球面坐标的公式是:
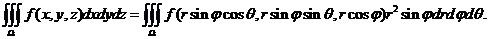
六、(本题满分7分)
【解析】证法一: 用拉格朗日中值定理来证明.
不妨设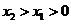 ,要证的不等式是
,要证的不等式是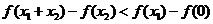 .
.
在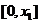 上用中值定理,有
上用中值定理,有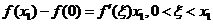 ;
;
在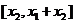 上用中值定理,又有
上用中值定理,又有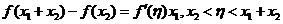
由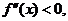 所以
所以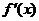 单调减,而
单调减,而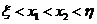 ,有
,有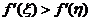 ,所以
,所以
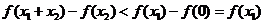 ,
,
即 .
.
证法二:用函数不等式来证明.要证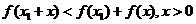 ,构造辅助函数
,构造辅助函数
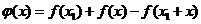 ,
,
则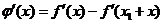 .由
.由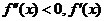 单调减,
单调减,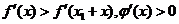 .
.
由此,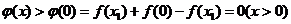 .改
.改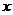 为
为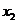 即得证.
即得证.
【相关知识点】拉格朗日中值定理:如果函数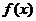 满足在闭区间
满足在闭区间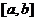 上连续,在开区间
上连续,在开区间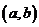 内可导,那么在
内可导,那么在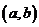 内至少有一点
内至少有一点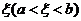 ,使等式
,使等式
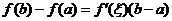
成立.
七、(本题满分8分)
【解析】(1)先求出在变力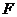 的作用下质点由原点沿直线运动到点
的作用下质点由原点沿直线运动到点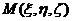 时所作的功
时所作的功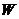 的表达式.点
的表达式.点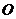 到点
到点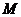 的线段记为
的线段记为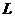 ,则
,则
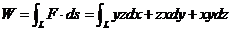 .
.
(2)计算曲线积分: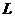 的参数方程是
的参数方程是 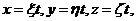
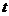 从
从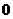 到
到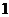 ,
,
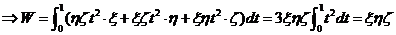 .
.
化为最值问题并求解:问题变成求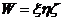 在条件
在条件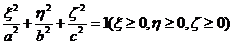 下的最大值与最大值点.
下的最大值与最大值点.
用拉格朗日乘子法求解.拉格朗日函数为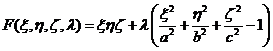 ,则有
,则有
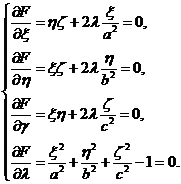
解此方程组:对前三个方程,分别乘以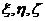 得
得 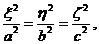 (
(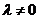 时)
时)
代入第四个方程得 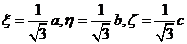 .
.
相应的 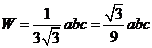 .当
.当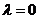 时相应的
时相应的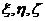 得
得 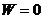 .
.
因为实际问题存在最大值,所以当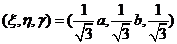 时
时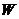 取最大值
取最大值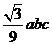 .
.
【相关知识点】拉格朗日乘子法:
要找函数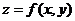 在附加条件
在附加条件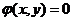 下的可能极值点,可以先作拉格朗日函数
下的可能极值点,可以先作拉格朗日函数
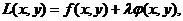
其中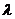 为参数.求其对
为参数.求其对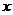 与
与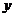 的一阶偏导数,并使之为零,然后与附加条件联立起来:
的一阶偏导数,并使之为零,然后与附加条件联立起来:
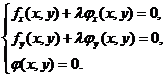
由这方程组解出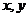 及
及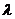 ,这样得到的
,这样得到的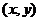 就是函数
就是函数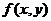 在附加条件
在附加条件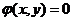 下的可能极值点.
下的可能极值点.
八、(本题满分7分)
【解析】(1) 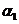 能由
能由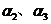 线性表出.
线性表出.
因为已知向量组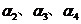 线性无关,所以
线性无关,所以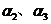 线性无关,又因为
线性无关,又因为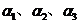 线性相关,故
线性相关,故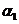 能由
能由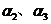 线性表出.
线性表出.
(2) 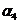 不能由
不能由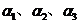 线性表出,
线性表出,
反证法:若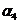 能由
能由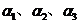 线性表出,设
线性表出,设 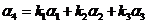 .
.
由(1)知, 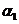 能由
能由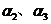 线性表出,可设
线性表出,可设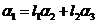 ,那么代入上式整理得
,那么代入上式整理得
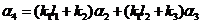 .
.
即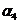 能由
能由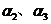 线性表出,从而
线性表出,从而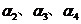 线性相关,这与已知矛盾.
线性相关,这与已知矛盾.
因此,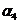 不能由
不能由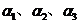 线性表出.
线性表出.
【相关知识点】向量组线性相关和线性无关的定义:存在一组不全为零的数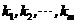 ,使
,使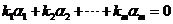 ,则称
,则称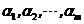 线性相关;否则,称
线性相关;否则,称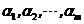 线性无关.
线性无关.
九、(本题满分7分)
【解析】(1)设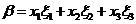 ,即是求此方程组的解.
,即是求此方程组的解.
对增广矩阵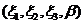 作初等行变换,
作初等行变换,
第一行乘以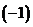 分别加到第二行和第三行上,再第二行乘以
分别加到第二行和第三行上,再第二行乘以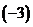 加到第三行上,第三行自乘
加到第三行上,第三行自乘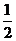 ,有
,有
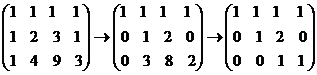 ,
,
第三行乘以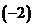 、
、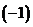 分别加到第二行和第一行上,再第二行乘以
分别加到第二行和第一行上,再第二行乘以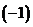 加到第一行上,有 增广矩阵
加到第一行上,有 增广矩阵 .
.
解出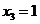 ,
,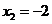 ,
,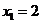 ,故
,故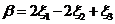 .
.
(2) 由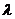 为
为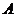 的特征值可知,存在非零向量
的特征值可知,存在非零向量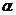 使
使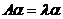 ,两端左乘
,两端左乘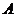 ,得
,得
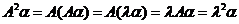 ,再一直这样操作下去,有
,再一直这样操作下去,有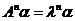 .
.
因为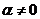 ,故
,故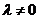 .按特征值定义知
.按特征值定义知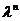 是
是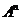 的特征值,且
的特征值,且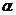 为相应的特征向量.
为相应的特征向量.
所以有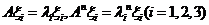 ,据(1)结论
,据(1)结论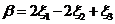 ,有
,有
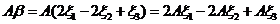 ,
,
于是 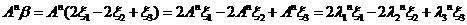
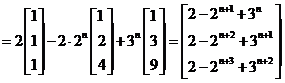 .
.
【相关知识点】矩阵特征值与特征向量的定义:设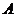 是
是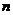 阶矩阵,若存在数
阶矩阵,若存在数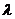 及非零的
及非零的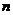 维列向量
维列向量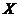 使得
使得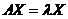 成立,则称
成立,则称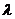 是矩阵
是矩阵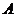 的特征值,称非零向量
的特征值,称非零向量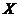 是矩阵
是矩阵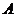 的特征向量.
的特征向量.
十、填空题(本题满分6分,每小题3分.)
【解析】由条件概率和乘法公式:从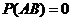 ,可知
,可知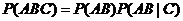
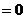 ,
,
由加法公式:
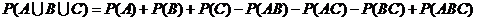
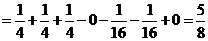 ,
,
故 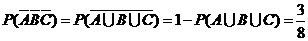 .
.
(2)【解析】依题意,随机变量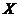 服从参数为
服从参数为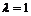 的指数分布,故
的指数分布,故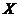 的概率密度为
的概率密度为
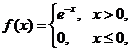
根据连续型随机变量函数的数学期望的求法,得出
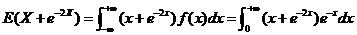
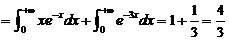 .
.
十一、(本题满分6分)
【解析】方法一:利用分布函数求密度函数:
首先,因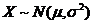 ,所以
,所以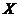 的密度函数为
的密度函数为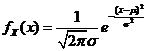 ,
,
因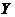 服从
服从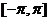 上的均匀分布,故
上的均匀分布,故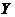 的密度函数为
的密度函数为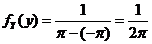 .
.
因为随机变量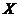 与
与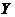 相互独立,所以二维随机变量
相互独立,所以二维随机变量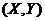 的联合概率密度为
的联合概率密度为
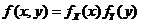 .要求
.要求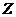 的密度函数,先求
的密度函数,先求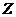 的分布函数
的分布函数
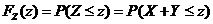
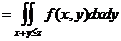
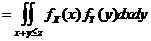
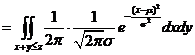 .
.
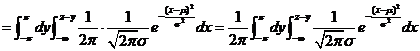
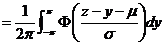 (由标准正态分布来表示一般正态分布)
(由标准正态分布来表示一般正态分布)
求出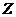 的分布函数,因此,对分布函数求导得密度函数,
的分布函数,因此,对分布函数求导得密度函数,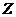 的密度函数为
的密度函数为
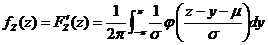
其中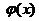 是标准正态分布的概率分布密度.由于
是标准正态分布的概率分布密度.由于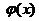 是偶函数,故有
是偶函数,故有
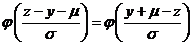
于是 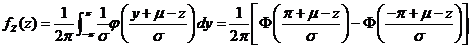 .
.
最终用标准正态分布函数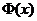 表示出来
表示出来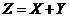 的概率分布密度.
的概率分布密度.
方法二:用卷积公式直接计算:
直接应用相互独立随机变量之和密度的卷积公式,求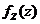 更为简单.
更为简单.
因为随机变量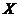 与
与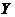 相互独立,由卷积公式
相互独立,由卷积公式
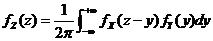
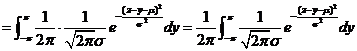
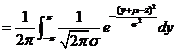
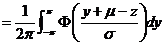
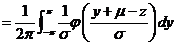
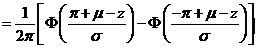 .
.
最终用标准正态分布函数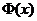 表示出来
表示出来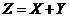 的概率分布密度.
的概率分布密度.