|
微信搜索关注"91考试网"公众号,领30元,获取公务员、事业编、教师等考试资料40G!
bsp; 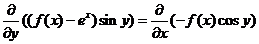 , ,
即 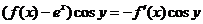 , ,
化简得 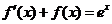 , 即 , 即 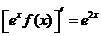 , ,
解之得 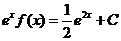 , 所以 , 所以 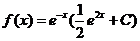 . .
由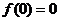 得 得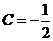 ,因此 ,因此 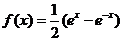 ,故应选(B). ,故应选(B).
【相关知识点】曲线积分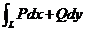 在单连通区域内与路径无关的充分必要条件是 在单连通区域内与路径无关的充分必要条件是
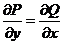 . .
(5)【答案】(C)
【解析】若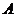 是 是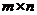 矩阵, 矩阵, 是 是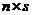 矩阵, 矩阵,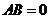 ,则 ,则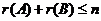 . .
当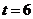 时,矩阵的三行元素对应成比例, 时,矩阵的三行元素对应成比例,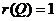 ,有 ,有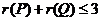 ,知 ,知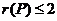 , ,
所以,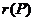 可能是1,也有可能是2,所以(A)、(B)都不准确; 可能是1,也有可能是2,所以(A)、(B)都不准确;
当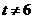 时,矩阵的第一行和第三行元素对应成比例, 时,矩阵的第一行和第三行元素对应成比例,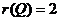 ,于是从 ,于是从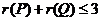 得 得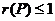 ,又因 ,又因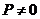 ,有 ,有 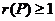 ,从而 ,从而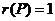 必成立,所以应当选(C). 必成立,所以应当选(C).
三、(本题共3小题,每小题5分,满分15分.)
(1)【解析】令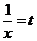 ,则当 ,则当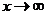 时, 时,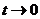 , ,
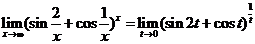 , ,
这是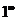 型未定式, 型未定式,
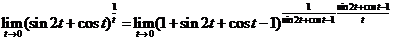 , ,
而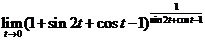 是两个重要极限之一,即 是两个重要极限之一,即
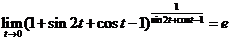 . .
所以 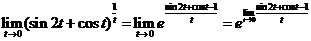 . .
而 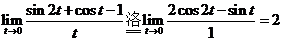 , ,
故 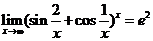 . .
(2)【解析】方法一: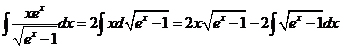 . .
令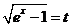 ,则 ,则 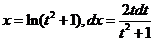 , ,
所以 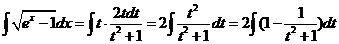
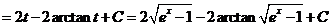 , ,
所以 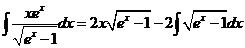
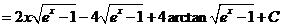 . .
方法二:令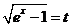 ,则 ,则 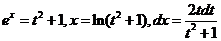 , ,
所以 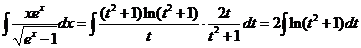
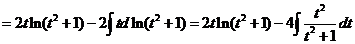 . .
关于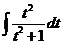 的求解同方法一,所以 的求解同方法一,所以
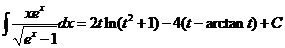
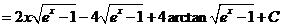 . .
(3)【解析】解法一:所给方程为伯努利方程,两边除以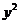 得 得
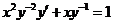 ,即 ,即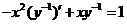 . .
令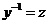 ,则方程化为 ,则方程化为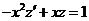 ,即 ,即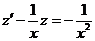 , ,
即 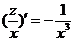 , ,
积分得 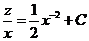 . .
由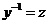 得 得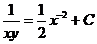 , ,
即 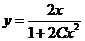 , ,
代入初始条件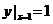 ,得 ,得 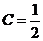 ,所以所求方程的特解是 ,所以所求方程的特解是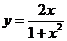 . .
解法二:所给方程可写成 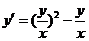 的形式,此方程为齐次方程. 的形式,此方程为齐次方程.
令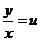 ,则 ,则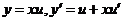 ,所以方程可化为 ,所以方程可化为
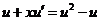 ,分离变量得 ,分离变量得 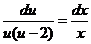 , ,
积分得 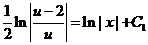 , 即 , 即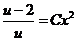 . .
以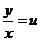 代入上式,得 代入上式,得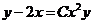 .代入初始条件 .代入初始条件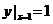 ,得 ,得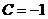 , ,
故特解为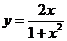 . .
四、(本题满分6分)
【解析】将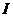 表成 表成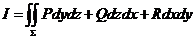 ,则 ,则
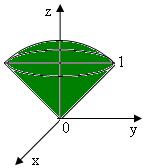 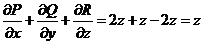 . .
又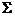 是封闭曲面,可直接用高斯公式计算. 是封闭曲面,可直接用高斯公式计算.
记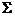 围成区域 围成区域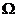 ,见草图, ,见草图,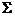 取外侧,由高斯公式得 取外侧,由高斯公式得
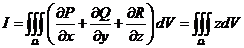 . .
用球坐标变换求这个三重积分.
在球坐标变换下, 为: 为: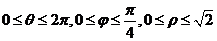 ,于是 ,于是
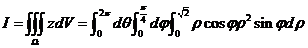
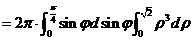
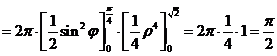 . .
五、(本题满分7分)
【解析】先将级数分解,
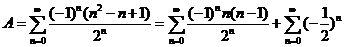 . .
第二个级数是几何级数,它的和已知
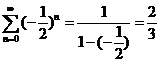 . .
求第一个级数的和转化为幂级数求和.考察
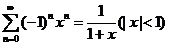 . .
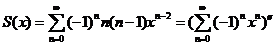 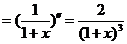 , ,
所以 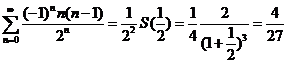 . .
因此原级数的和 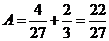 . .
六、(本题共2小题,每小题5分,满分10分.)
(1)【解析】证法一:由拉格朗日中值定理可知,在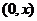 存在一点 存在一点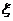 ,使得 ,使得
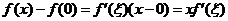 , ,
即 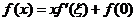 . .
因为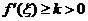 ,所以当 ,所以当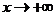 时, 时,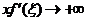 ,故 ,故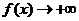 . .
由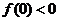 ,所以在 ,所以在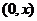 上由介值定理可知,必有一点 上由介值定理可知,必有一点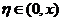 使得 使得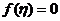 . .
又因为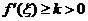 ,故 ,故 为严格单调增函数,故 为严格单调增函数,故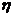 值唯一. 值唯一.
证法二:用牛顿-莱布尼兹公式,由于
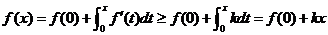 , ,
以下同方法1.
(2)【解析】先将不等式做恒等变形:
因为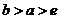 ,故原不等式等价于 ,故原不等式等价于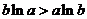 或 或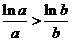 . .
证法一:令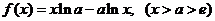 ,则 ,则 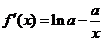 . .
因为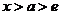 ,所以 ,所以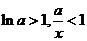 ,故 ,故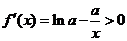 . .
从而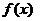 在 在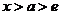 时为严格的单调递增函数,故 时为严格的单调递增函数,故 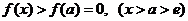 . .
由此 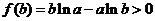 ,即 ,即 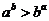 . .
证法二:令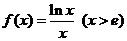 ,则 ,则 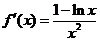 . .
当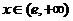 时, 时,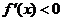 ,所以 ,所以 为严格的单调递减函数,故存在 为严格的单调递减函数,故存在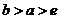 使得 使得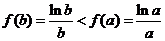
成立.即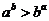 . .
七、(本题满分8分)
【解析】写出二次型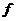 的矩阵为 的矩阵为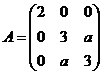 ,它的特征方程是 ,它的特征方程是
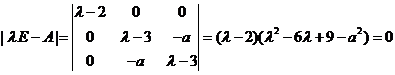 . .
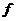 经正交变换化成标准形 经正交变换化成标准形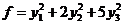 ,那么标准形中平方项的系数1,2,5就是 ,那么标准形中平方项的系数1,2,5就是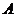 的特征值. 的特征值.
把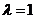 代入特性方程,得 代入特性方程,得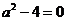 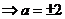 . .
因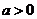 知 知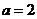 .这时 .这时 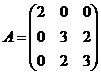 . .
对于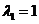 ,由 ,由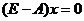 , , 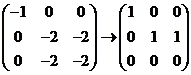 ,得 ,得 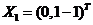 . .
对于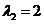 ,由 ,由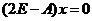 , ,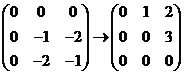 ,得 ,得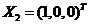 . .
对于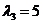 ,由 ,由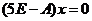 , ,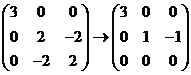 ,得 ,得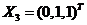 . .
将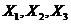 单位化,得 单位化,得
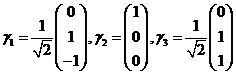 . .
故所用的正交变换矩阵为
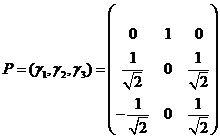 . .
【相关知识点】二次型的定义:含有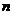 个变量 个变量 的二次齐次多项式(即每项都是二次的多项式) 的二次齐次多项式(即每项都是二次的多项式)
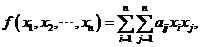 其中 其中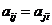 , ,
称为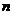 元二次型.令 元二次型.令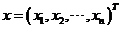 , ,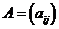 ,则二次型可用矩阵乘法表示为 ,则二次型可用矩阵乘法表示为
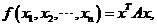
其中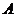 是对称矩阵 是对称矩阵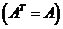 ,称 ,称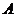 为二次型 为二次型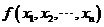 的矩阵. 的矩阵.
八、(本题满分6分)
【解析】证法一:对 按列分块,记 按列分块,记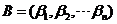 ,若 ,若
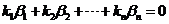 , ,
即 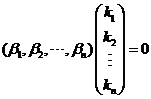 , 亦即 , 亦即 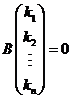 . .
两边左乘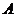 ,得 ,得 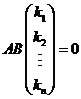 ,即 ,即 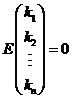 ,亦即 ,亦即 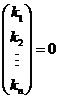 . .
所以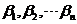 线性无关. 线性无关.
证法二:因为 是 是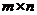 矩阵, 矩阵,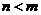 ,所以 ,所以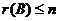 . .
又因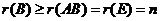 ,故 ,故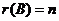 .所以 .所以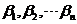 线性无关. 线性无关.
【相关知识点】1. 向量组线性相关和线性无关的定义:存在一组不全为零的数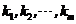 ,使 ,使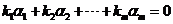 ,则称 ,则称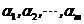 线性相关;否则,称 线性相关;否则,称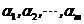 线性无关. 线性无关.
2. 矩阵乘积秩的结论:乘积的秩小于等于单个矩阵的秩
九、(本题满分6分)
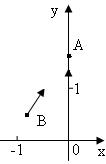 【解析】如图,设当 【解析】如图,设当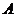 运动到 运动到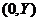 时, 时, 运动到 运动到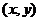 . .
由 的方向始终指向 的方向始终指向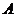 ,有 ,有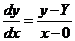 ,即 ,即
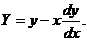 (1) (1)
又由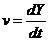 , ,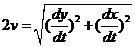 ,得 ,得
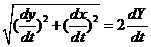 . .
由题意,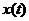 单调增, 单调增,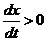 ,所以 ,所以 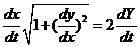 .亦即 .亦即
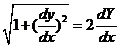 . (2) . (2)
由(1),(2)消去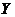 , ,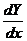 ,便得微分方程 ,便得微分方程 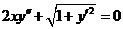 . .
初始条件显然是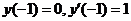 . .
十、填空题(本题共2小题,每小题3分,满分6分,把答案填在题中横线上.)
(1)【解析】可以用古典概型,也可以用抽签原理.
方法一:从直观上看,第二次抽出次品的可能性与第一次抽到正品还是次品有关,所以考虑用全概率公式计算.
设事件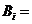 “第 “第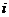 次抽出次品” 次抽出次品”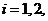 由已知得 由已知得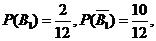
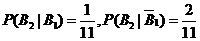 .应用全概率公式 .应用全概率公式
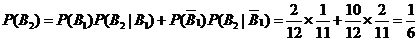 . .
方法二:对填空题和选择题可直接用抽签原理得到结果.
由抽签原理(抽签与先后次序无关),不放回抽样中第二次抽得次品的概率与第一次抽得次品的概率相同,都是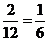 . .
(2)【解析】方法一:可以用分布函数法,即先求出分布函数,再求导得到概率密度函数.
由已知条件,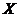 在区间 在区间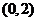 上服从均匀分布,得 上服从均匀分布,得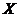 的概率密度函数为 的概率密度函数为
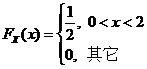 . .
先求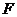 的分布函数 的分布函数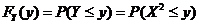 . .
当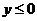 时, 时,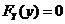 ;当 ;当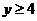 时, 时,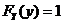 ;当 ;当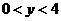 时, 时,
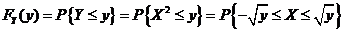
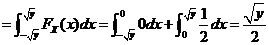 . .
即 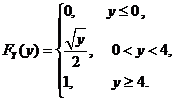
于是,对分布函数求导得密度函数
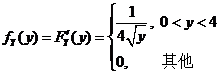 . .
故随机变量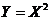 在 在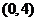 内的概率分布密度 内的概率分布密度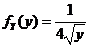 . .
方法二:也可以应用单调函数公式法.
由于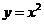 在(0,4)内单调,反函数 在(0,4)内单调,反函数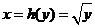 在(0,2)内可导,且导数 在(0,2)内可导,且导数
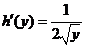 恒不为零,因此,由连续型随机变量函数的密度公式,得到随机变量 恒不为零,因此,由连续型随机变量函数的密度公式,得到随机变量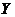 的概率密度为 的概率密度为
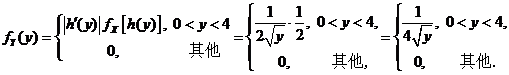
故随机变量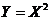 在 在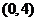 内的概率分布密度 内的概率分布密度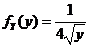 . .
十一、(本题满分6分)
【解析】(1)第一问是常规问题,直接运用公式对其计算可得期望与方差.
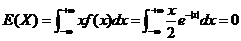 . .
(因为被积函数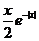 是奇函数,积分区域关于 是奇函数,积分区域关于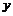 轴对称,所以积分值为0.) 轴对称,所以积分值为0.)
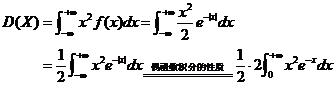
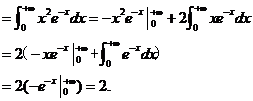
(2) 根据协方差的计算公式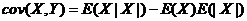 来计算协方差. 来计算协方差.
因为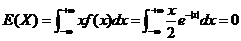 ,所以 ,所以
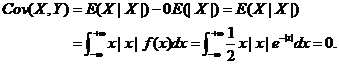
(因为被积函数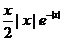 是奇函数,积分区域关于 是奇函数,积分区域关于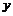 轴对称,所以积分值为0.) 轴对称,所以积分值为0.)
所以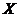 与 与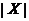 不相关. 不相关.
(3) 方法一:
对于任意正实数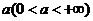 ,事件 ,事件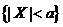 含于事件 含于事件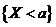 ,且 ,且
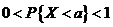 , ,
所以 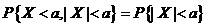 , ,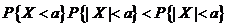 , ,
可见 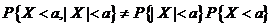 , ,
因此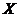 与 与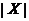 不独立. 不独立.
方法二:因为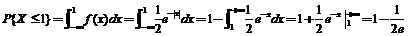 ; ;
又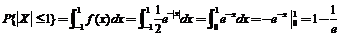 ,显然有 ,显然有
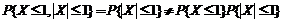 ,因此 ,因此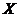 与 与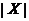 不独立. 不独立.
|