微信搜索关注"91考试网"公众号,领30元,获取公务员、事业编、教师等考试资料40G!
2006年全国硕士研究生入学统一考试数学一试题
一、填空题:1-6小题,每小题4分,共24分,请将答案写在答题纸指定位置上.
(1) 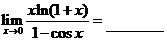 .
.
(2) 微分方程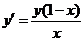 的通解是 .
的通解是 .
(3) 设 是锥面
是锥面 (
(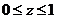 )的下侧,则
)的下侧,则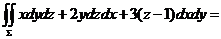
.
(4) 点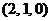 到平面
到平面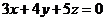 的距离
的距离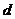 = .
= .
(5) 设矩阵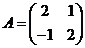 ,
,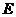 为
为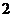 阶单位矩阵,矩阵
阶单位矩阵,矩阵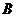 满足
满足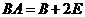 ,则
,则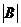 = .
= .
(6)设随机变量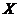 与
与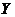 相互独立,且均服从区间
相互独立,且均服从区间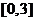 上的均匀分布,则
上的均匀分布,则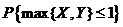 = .
= .
二、选择题:9-14小题,每小题4分,共32分,下列每小题给出的四个选项中,只有一项符合题目要求,把所选项前的字母填在题后的括号内.
(7) 设函数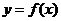 具有二阶导数,且
具有二阶导数,且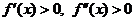 ,
,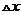 为自变量
为自变量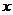 在
在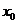 处的增量,
处的增量,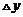 与
与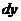 分别为
分别为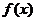 在点
在点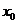 处对应的增量与微分,若
处对应的增量与微分,若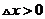 ,则( )
,则( )
(A)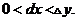 (B)
(B)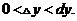
(C)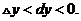 (D)
(D)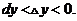
(8) 设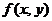 为连续函数,则
为连续函数,则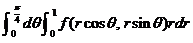 等于( )
等于( )
(A)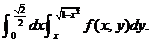 (B)
(B)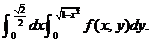
(C)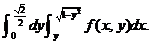 (D)
(D)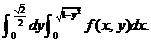
(9) 若级数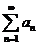 收敛,则级数( )
收敛,则级数( )
(A)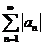 收敛. (B)
收敛. (B)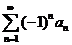 收敛.
收敛.
(C)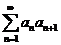 收敛. (D)
收敛. (D)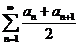 收敛.
收敛.
(10) 设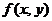 与
与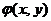 均为可微函数,且
均为可微函数,且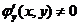 . 已知
. 已知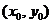 是
是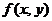 在约束条件
在约束条件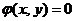 下的一个极值点,下列选项正确的是( )
下的一个极值点,下列选项正确的是( )
(A)若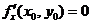 ,则
,则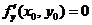 .
.
(B)若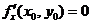 ,则
,则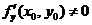 .
.
(C)若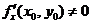 ,则
,则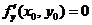 .
.
(D)若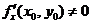 ,则
,则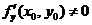 .
.
(11) 设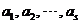 均为
均为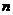 维列向量,
维列向量,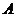 是
是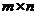 矩阵,下列选项正确的是( )
矩阵,下列选项正确的是( )
(A)若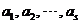 线性相关,则
线性相关,则 线性相关.
线性相关.
(B)若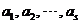 线性相关,则
线性相关,则 线性无关.
线性无关.
(C)若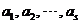 线性无关,则
线性无关,则 线性相关.
线性相关.
(D)若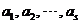 线性无关,
线性无关, 线性无关.
线性无关.
(12) 设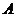 为3阶矩阵,将
为3阶矩阵,将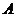 的第2行加到第1行得
的第2行加到第1行得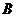 ,再将
,再将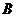 的第1列的-1倍加到第2列得
的第1列的-1倍加到第2列得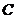 ,记
,记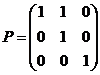 ,则( )
,则( )
(A)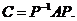 (B)
(B)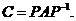
(C)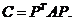 (D)
(D)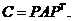
(13) 设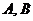 为随机事件,且
为随机事件,且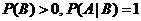 ,则必有( )
,则必有( )
(A)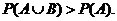 (B)
(B)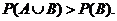
(C)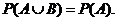 (D)
(D)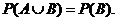
(14) 设随机变量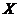 服从正态分布
服从正态分布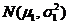 ,
,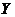 服从正态分布
服从正态分布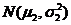 ,且
,且
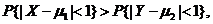 则必有( )
则必有( )
(A)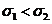 (B)
(B)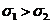
(C)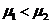 (D)
(D)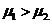
三、解答题:15-23小题,共94分.请将解答写在答题纸指定的位置上.解答应写出文字说明、证明过程或演算步骤.
(15)(本题满分10分)
设区域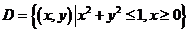 ,计算二重积分
,计算二重积分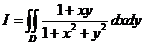 .
.
(16)(本题满分12分)
设数列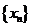 满足
满足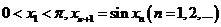 .
.
(I)证明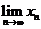 存在,并求该极限 ;
存在,并求该极限 ;
(II)计算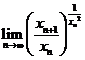 .
.
(17)(本题满分12分)
将函数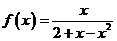 展开成
展开成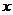 的幂级数 .
的幂级数 .
(18)(本题满分12分)
设函数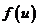 在
在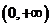 内具有二阶导数,且
内具有二阶导数,且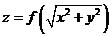 满足等式
满足等式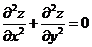
(I) 验证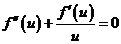 .
.
(II) 若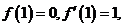 求函数
求函数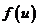 的表达式.
的表达式.
(19)(本题满分12分)
设在上半平面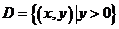 内,函数
内,函数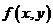 是有连续偏导数,且对任意的
是有连续偏导数,且对任意的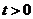 都有
都有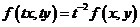 .
.
证明: 对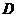 内的任意分段光滑的有向简单闭曲线
内的任意分段光滑的有向简单闭曲线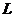 ,都有
,都有 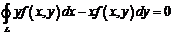
(20)(本题满分9分)
已知非齐次线性方程组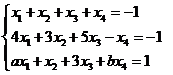 有
有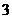 个线性无关的解
个线性无关的解
(I) 证明方程组系数矩阵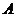 的秩
的秩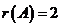 ;
;
(II) 求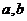 的值及方程组的通解.
的值及方程组的通解.
(21)(本题满分9分)
设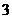 阶实对称矩阵
阶实对称矩阵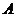 的各行元素之和均为
的各行元素之和均为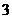 ,向量
,向量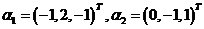 是线性方程组
是线性方程组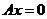 的两个解.
的两个解.
(I) 求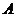 的特征值与特征向量
的特征值与特征向量
(II) 求正交矩阵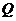 和对角矩阵
和对角矩阵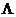 ,使得
,使得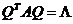 .
.
(22)(本题满分9分)
随机变量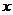 的概率密度为
的概率密度为 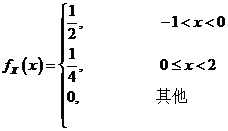
 为二维随机变量
为二维随机变量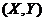 的分布函数.求
的分布函数.求
(I)  的概率密度
的概率密度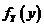 ; (II)
; (II) 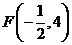 .
.
(23)(本题满分9分)
设总体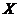 的概率密度为
的概率密度为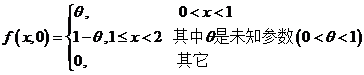 .
. 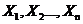 为来自总体
为来自总体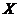 的简单随机样本,记
的简单随机样本,记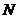 为样本值
为样本值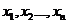 中小于
中小于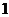 的个数,求
的个数,求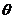 的最大似然估计.
的最大似然估计.
2006年全国硕士研究生入学统一考试数学一试题解析
一、填空题
(1)【答案】2.
【详解】由等价无穷小替换,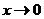 时,
时,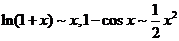 ,
,
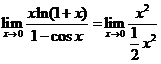 =2
=2
(2)