|
E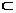 Rn上可测. Rn上可测.
11.设f(x)在E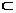 Rn上Riemann可积,则f(x)在E Rn上Riemann可积,则f(x)在E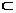 Rn上Lebesgue可积. Rn上Lebesgue可积.
12.[a,b]上单调函数f(x)的导函数f /(x)在[a,b]上可积.
非选择题部分
注意事项:
用黑色字迹的签字笔或钢笔将答案写在答题纸上,不能答在试题卷上。
三、填空题(本大题共8小题,每小题4分,共32分)
13.设集列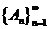 满足An 满足An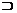 An+1(n=1,2,…),则 An+1(n=1,2,…),则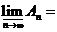 _________. _________.
14.设E是[0,1]中的全部有理点, 则E在R2的边界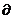 E=_________. E=_________.
15.设E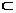 Rn是Lebesgue可测集,则对任意的集合T,m*(T∩E)+m*(T∩CE)=_________. Rn是Lebesgue可测集,则对任意的集合T,m*(T∩E)+m*(T∩CE)=_________.
16.设f(x)在E上可测,则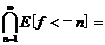 _________. _________.
17.设f(x)在E Rn上Lebesgue可积,f+(x),f-(x)分别表示f (x)的正部与负部,且 Rn上Lebesgue可积,f+(x),f-(x)分别表示f (x)的正部与负部,且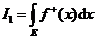 , , 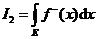 , 则 , 则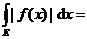 _________. _________.
18.设fn(x)(n=1,2,…)是可测集E上一列非负可测函数,记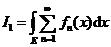 , ,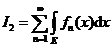 ,则它们的大小关系是_________. ,则它们的大小关系是_________.
19.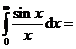 _________. _________.
20.设f(x)=kx+b,k>0, 0≤x≤1, 则f (x)的全变差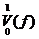 =_________. =_________.
四、完成下列各题(本大题共3小题,每小题9分,共27分)
21.设E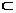 Rp是Lebesgue可测集,证明对任意ε>0,存在开集G Rp是Lebesgue可测集,证明对任意ε>0,存在开集G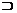 E,使得m(G-E)<ε. E,使得m(G-E)<ε.
22.设E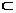 R, f (x)是E上a.e有限的可测函数,证明存在R上一列连续函数{gn(x)}s.t. R, f (x)是E上a.e有限的可测函数,证明存在R上一列连续函数{gn(x)}s.t.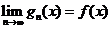 a.e于E. a.e于E.
23.设D={(x,y)|0≤x≤1;0≤y≤1},在D定义函数
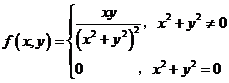 , ,
证明f(x,y)在D上不可积.
|