|
微信搜索关注"91考试网"公众号,领30元,获取公务员、事业编、教师等考试资料40G!
项公式。
20.(本小题满分14分)已知椭圆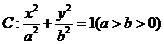 的一个焦点为 的一个焦点为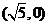 ,离心率为 ,离心率为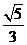 , ,
(1)求椭圆C的标准方程;
(2)若动点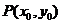 为椭圆外一点,且点P到椭圆C的两条切线相互垂直,求点P的轨迹方程。 为椭圆外一点,且点P到椭圆C的两条切线相互垂直,求点P的轨迹方程。
21.(本小题满分14分) 设函数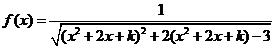 ,其中 ,其中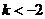 , ,
(1)求函数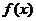 的定义域D(用区间表示); 的定义域D(用区间表示);
(2)讨论函数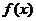 在D上的单调性; 在D上的单调性;
(3)若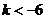 ,求D上满足条件 ,求D上满足条件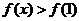 的 的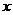 的集合(用区间表示)。 的集合(用区间表示)。
2014年普通高等学校招生全国统一考试(广东卷)
数学(理科)参考答案 成本文 6/8/2014
1-8:CDBA BADD;
8.解:A中元素为有序数组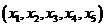 ,题中要求有序数组的5个数中仅1个数为 ,题中要求有序数组的5个数中仅1个数为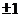 、仅2个数为 、仅2个数为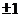 或仅3个数为 或仅3个数为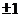 ,所以共有 ,所以共有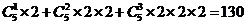 个不同数组; 个不同数组;
9.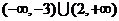 ; 10. ; 10.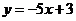 ; 11. ; 11.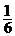 ; 12.2; 13.50; 14.(1,1); 15.9; ; 12.2; 13.50; 14.(1,1); 15.9;
11.解:6之前6个数中取3个,6之后3个数中取3个,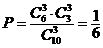 ; ;
16.解:(1) , ,
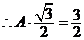 , ,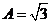 ; ;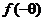 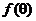
(2)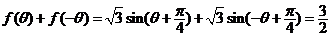 , ,
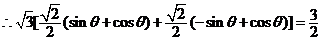 , ,
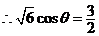 , ,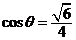 ,又 ,又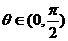 , ,
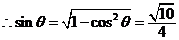 , ,
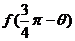 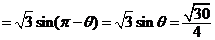 . .
17. 解:(1)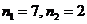 , ,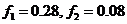 ; ;
(2)样本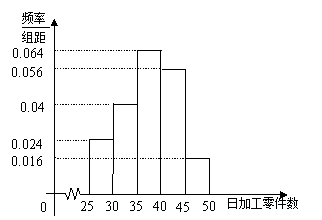 频率分布直方图为 频率分布直方图为

(3)根据样本频率分布直方图,每人的日加工零件数落在区间(30,35]的概率0.2,
设所取的4人中,日加工零件数落在区间(30,35]的人数为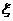 ,则 ,则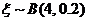 , ,
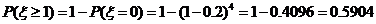 , ,
所以4人中,至少有1人的日加工零件数落在区间(30,50]的概率约为0.5904.
18.(1) 平面 平面 , ,
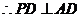 ,又 ,又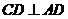 , ,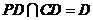 , ,
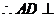 平面 平面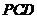 , ,
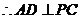 ,又 ,又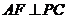 , ,
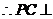 平面 平面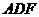 ,即 ,即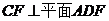 ; ;
(2)设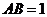 ,则 ,则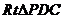 中, 中,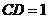 ,又 ,又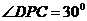 , ,
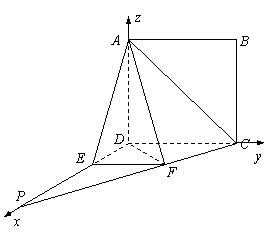 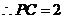 , ,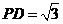 ,由(1)知 ,由(1)知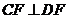
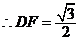 , ,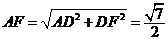 , ,
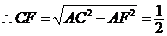 ,又 ,又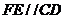 , ,
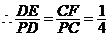 , ,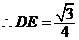 ,同理 ,同理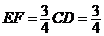 , ,
如图所示,以D为原点,建立空间直角坐标系,则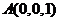 , ,
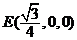 , ,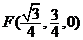 , ,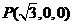 , ,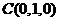 , ,
设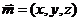 是平面 是平面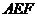 的法向量,则 的法向量,则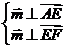 ,又 ,又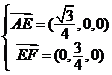 , ,
所以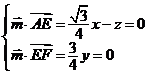 ,令 ,令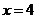 ,得 ,得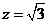 , ,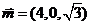 , ,
由(1)知平面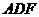 的一个法向量 的一个法向量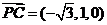 , ,
设二面角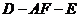 的平面角为 的平面角为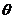 ,可知 ,可知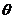 为锐角, 为锐角,
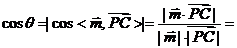 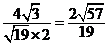 ,即所求. ,即所求.
19.解: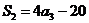 , ,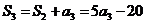 ,又 ,又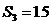 , ,
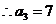 , ,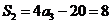 ,又 ,又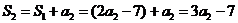 , ,
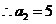 , ,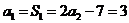 , ,
综上知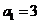 , ,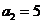 , ,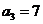 ; ;
(2)由(1)猜想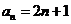 ,学科网下面用数学归纳法证明. ,学科网下面用数学归纳法证明.
①当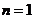 时,结论显然成立; 时,结论显然成立;
②假设当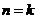 ( (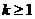 )时, )时,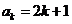 , ,
则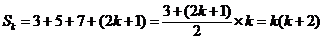 ,又 ,又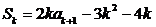 , ,
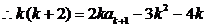 ,解得 ,解得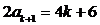 , ,
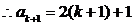 ,即当 ,即当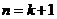 时,结论成立; 时,结论成立;
由①②知,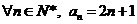 . .
20.解:(1)可知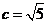 ,又 ,又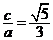 , ,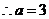 , ,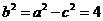 , ,
椭圆C的标准方程为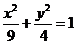 ; ;
(2)设两切线为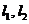 , ,
①当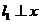 轴或 轴或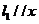 轴时,对应 轴时,对应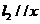 轴或 轴或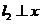 轴,可知 轴,可知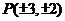
②当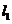 与 与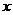 轴不垂直且不平行时, 轴不垂直且不平行时,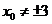 ,设 ,设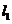 的斜率为 的斜率为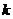 ,则 ,则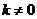 , ,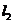 的斜率为 的斜率为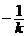 , ,
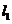 的方程为 的方程为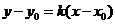 ,联立 ,联立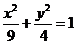 , ,
得 , ,
因为直线与椭圆相切,学科网所以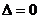 ,得 ,得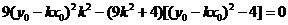 , ,
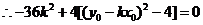 , ,
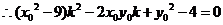
所以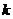 是方程 是方程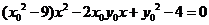 的一个根, 的一个根,
同理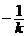 是方程 是方程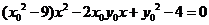 的另一个根, 的另一个根,
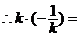 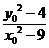 ,得 ,得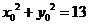 ,其中 ,其中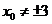 , ,
所以点P的轨迹方程为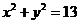 ( (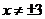 ), ),
因为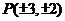 满足上式,综上知:点P的轨迹方程为 满足上式,综上知:点P的轨迹方程为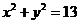 . .
21.解:(1)可知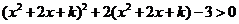 , ,
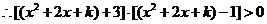 , ,
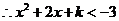 或 或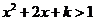 , ,
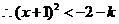 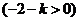 或 或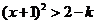 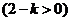 , ,
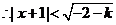 或 或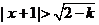 , ,
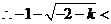 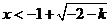 或 或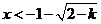 或 或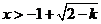 , ,
所以函数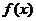 的定义域D为 的定义域D为
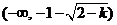 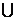 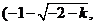 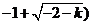 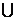 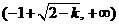 ; ;
(2)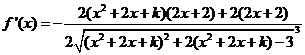 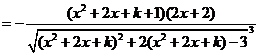 , ,
由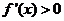 得 得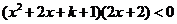 ,即 ,即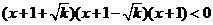 , ,
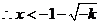 或 或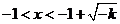 ,结合定义域知 ,结合定义域知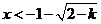 或 或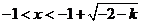 , ,
所以函数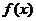 的学科网单调递增区间为 的学科网单调递增区间为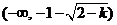 , ,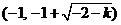 , ,
同理递减区间为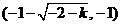 , ,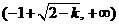 ; ;
(3)由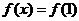 得 得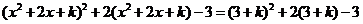 , ,
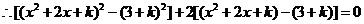 , ,
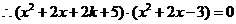 , ,
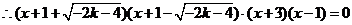 , ,
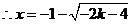 或 或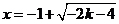 或 或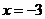 或 或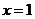 , ,
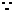 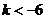 , ,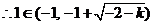 , ,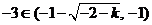 , ,
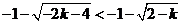 , ,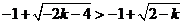 , ,
结合函数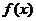 的单调性知 的单调性知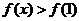 的解集为 的解集为
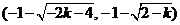  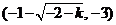  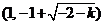 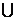 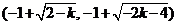 . .
|