|
微信搜索关注"91考试网"公众号,领30元,获取公务员、事业编、教师等考试资料40G!
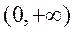 单调递增,而 单调递增,而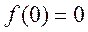 , ,
则当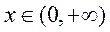 时, 时,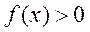 ,符合题意; ,符合题意;
当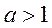 时, 时,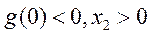 ,所以函数 ,所以函数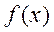 在 在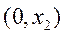 单调递减,而 单调递减,而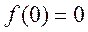 , ,
则当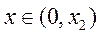 时, 时,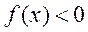 ,不符合题意; ,不符合题意;
当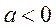 时,设 时,设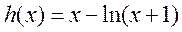 ,当 ,当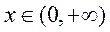 时 时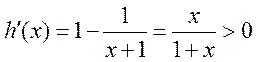 , ,
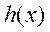 在 在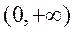 单调递增,因此当 单调递增,因此当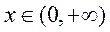 时 时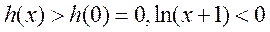 , ,
于是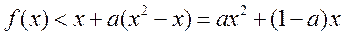 ,当 ,当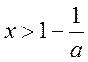 时 时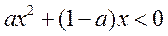 , ,
此时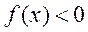 ,不符合题意. ,不符合题意.
综上所述,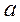 的取值范围是 的取值范围是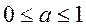 . .
另解:(Ⅰ)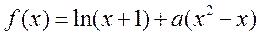 ,定义域为 ,定义域为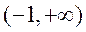
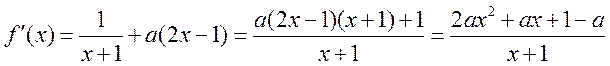 , ,
当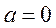 时, 时,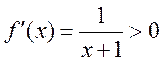 ,函数 ,函数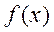 在 在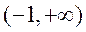 为增函数,无极值点. 为增函数,无极值点.
设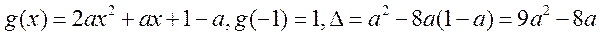 , ,
当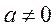 时,根据二次函数的图像和性质可知 时,根据二次函数的图像和性质可知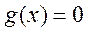 的根的个数就是函数 的根的个数就是函数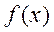 极值点的个数. 极值点的个数.
若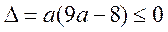 ,即 ,即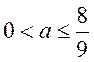 时, 时,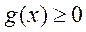 , ,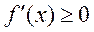 函数在 函数在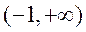 为增函数,无极值点. 为增函数,无极值点.
若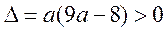 ,即 ,即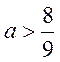 或 或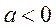 , ,
而当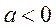 时 时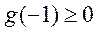 此时方程 此时方程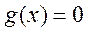 在 在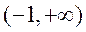 只有一个实数根,此时函数 只有一个实数根,此时函数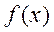 只有一个极值点; 只有一个极值点;
当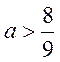 时方程 时方程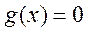 在 在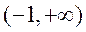 都有两个不相等的实数根,此时函数 都有两个不相等的实数根,此时函数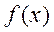 有两个极值点; 有两个极值点;
综上可知当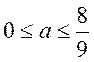 时 时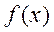 的极值点个数为0;当 的极值点个数为0;当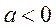 时 时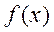 的极值点个数为1;当 的极值点个数为1;当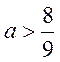 时, 时,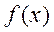 的极值点个数为2. 的极值点个数为2.
(Ⅱ)设函数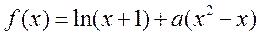 , ,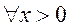 ,都有 ,都有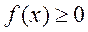 成立. 成立.
即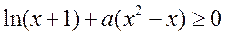
当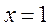 时, 时,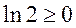 恒成立; 恒成立;
当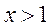 时, 时,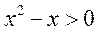 , ,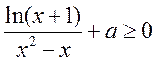 ; ;
当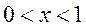 时, 时,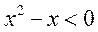 , ,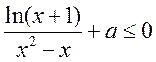 ;由 ;由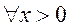 均有 均有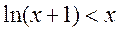 成立。 成立。
故当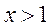 时,, 时,,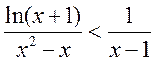 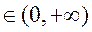 ,则只需 ,则只需 ; ;
当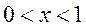 时, 时,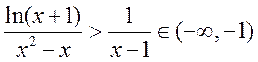 ,则需 ,则需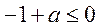 ,即 ,即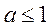 .综上可知对于 .综上可知对于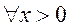 ,都有 ,都有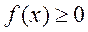 成立,只需 成立,只需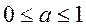 即可,故所求 即可,故所求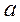 的取值范围是 的取值范围是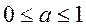 . .
另解:设函数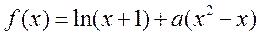 , ,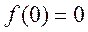 ,要使 ,要使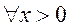 ,都有 ,都有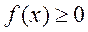 成立,只需函数函数 成立,只需函数函数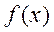 在 在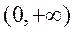 上单调递增即可, 上单调递增即可,
于是只需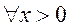 , ,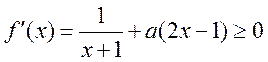 成立, 成立,
当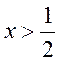 时 时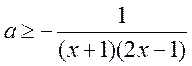 ,令 ,令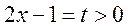 , ,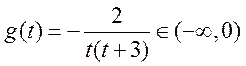 , ,
则 ;当 ;当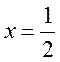 时 时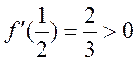 ;当 ;当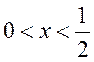 , ,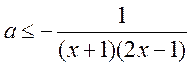 , ,
令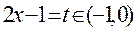 , ,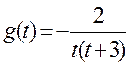 关于 关于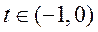 单调递增,则 单调递增,则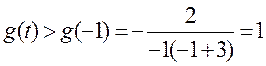 ,则 ,则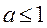 ,于是 ,于是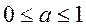 . .
又当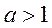 时, 时,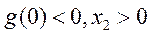 ,所以函数 ,所以函数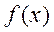 在 在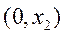 单调递减,而 单调递减,而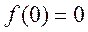 , ,
则当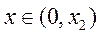 时, 时,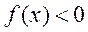 ,不符合题意; ,不符合题意;
当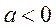 时,设 时,设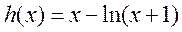 ,当 ,当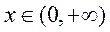 时 时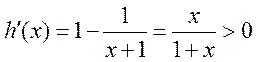 , ,
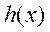 在 在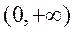 单调递增,因此当 单调递增,因此当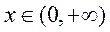 时 时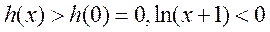 , ,
于是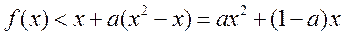 ,当 ,当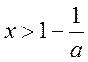 时 时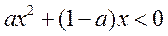 , ,
此时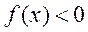 ,不符合题意. ,不符合题意.
综上所述,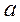 的取值范围是 的取值范围是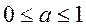 . .  
  


|