微信搜索关注"91考试网"公众号,领30元,获取公务员、事业编、教师等考试资料40G!
绝密★启用前
2015年普通高等学校招生全国统一考试(山东卷)
理科数学
本试卷分第Ⅰ卷和第Ⅱ卷两部分,共4页。满分150分。考试用时120分钟。考试结束后,将将本试卷和答题卡一并交回。
注意事项:
1.答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、座号、考生号县区和科类填写在答题卡和试卷规定的位置上。
2.第Ⅰ卷每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑;如需改动,用橡皮擦干净后,在选涂其他答案标号。答案卸载试卷上无效。
3. 第Ⅱ卷必须用0.5毫米黑色签字笔作答,答案必须写在答题卡各题目指定区域内相应的位置,不能写在试卷上;如需改动,先划掉原来的答案,然后再写上新的答案;不能使用涂改液、胶带纸、修正带。不按以上要求作答的答案无效。
4.填空题直接填写答案,解答题应写出文字说明、证明过程或演算步骤.
参考公式:
如果事件A,B互斥,那么P(A+B)=P(A)+P(B).
第Ⅰ卷(共50分)
一、 选择题:本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合要求的
(1) 已知集合A={X|X²-4X+3<0},B={X|2<X<4},则A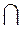 B=
B=
(A)(1,3) (B)(1,4) (C)(2,3) (D)(2,4)
(2)若复数Z满足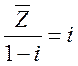 ,其中i为虚数为单位,则Z=
,其中i为虚数为单位,则Z=
(A)1-i (B)1+i (C)-1-i (D)-1+i
(3)要得到函数y=sin(4x-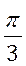 )的图像,只需要将函数y=sin4x的图像()
)的图像,只需要将函数y=sin4x的图像()
(A)向左平移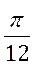 个单位 (B)向右平移
个单位 (B)向右平移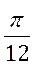 个单位
个单位
(C)向左平移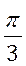 个单位 (D)向右平移
个单位 (D)向右平移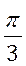 个单位
个单位
(4)已知ABCD 的边长为a,∠ABC=60o ,则 .
.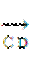 =
=
(A)- 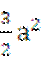 (B)-
(B)- 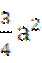 (C)
(C) 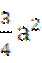 (D)
(D) 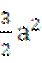
(5)不等式|X-1|-|X-5|<2的解集是
(A)(-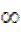 ,4) (B)(-
,4) (B)(-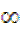 ,1)
,1)
(C)(1,4) (D)(1,5)
(6)已知x,y满足约束条件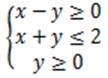 ,若z=ax+y的最大值为4,则a=
,若z=ax+y的最大值为4,则a=
(A)3 (B)2 (C)-2 (D)-3
(7)在梯形ABCD中,∠ABC= ,AD//BC,BC=2AD=2AB=2.将梯形ABCD绕AD所在的直线旋转一周而形成的曲面所围成的几何体的体积为
,AD//BC,BC=2AD=2AB=2.将梯形ABCD绕AD所在的直线旋转一周而形成的曲面所围成的几何体的体积为
(A)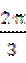 (B)
(B)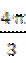 (C)
(C) 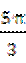 (D)2
(D)2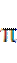
(8)已知某批零件的长度误差(单位:毫米)服从正态分布N(0,3),从中随机取一件,其长度误差落在区间(3,6)内的概率为
(附:若随机变量ξ服从正态分布N(μ,σ²)),则P(μ-σ<ξ<μ+σ)=68.26%,
P(μ-2σ<ξ<μ+2σ)=95.44%.)
(A)4.56% (B)13.59% (C)27.18% (D)31.74%
(9)一条光纤从点(-2,-3)射出,经y轴反射后与圆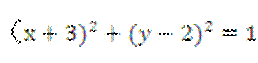 相切,则反射光线所在直线的斜率为()
相切,则反射光线所在直线的斜率为()
(A)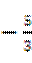 或
或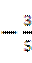 (B
(B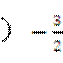 或
或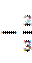
(C)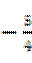 或
或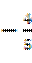 (D)
(D)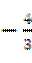 或
或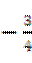
(10)设函数f(x)=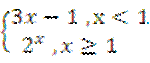 ,则满足f(f(a))=
,则满足f(f(a))=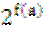 的a取值范围是()
的a取值范围是()
(A)[ ,1] (B)[0,1]
,1] (B)[0,1]
(C)[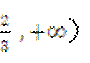 (D)[1,+
(D)[1,+
第Ⅱ卷(共100分)
二、 填空题:本大题共5小题,每小题5分,共25分。
(11)观察下列各式:
C10 =40
=40
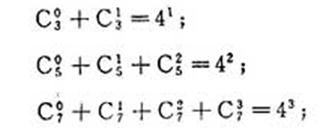
……
照此规律,当n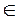 N时,
N时,
C02n-1 + C12n-1 + C22n-1 +…+ Cn-12n-1 = .
(12)若“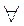 x
x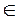 [0,
[0,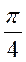 ],tanx
],tanx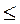 m”是真命题,则实数m的最小值为 .
m”是真命题,则实数m的最小值为 .
(13)执行右边的程序框图,输出的T的值为 .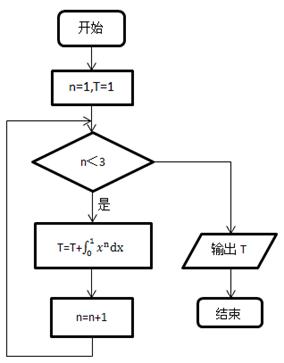
(14)已知函数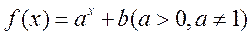 的定义域和值域都是
的定义域和值域都是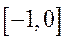 ,则
,则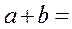
(15)平面直角坐标系xOy中,双曲线C1: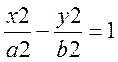 (a>0,b>0)的渐近线与抛物线
(a>0,b>0)的渐近线与抛物线
C2:X2=2py(p>0)交于O,若△OAB的垂心为C2的焦点,则C1的离心率为 ___
三、解答题:本答题共6小题,共75分。
(16)(本小题满分12分)
设f(x)=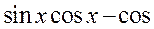 2(x+
2(x+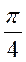 ).
).
(Ⅰ)求f(x)的单调区间;
(Ⅱ)在锐角△ABC中,角A,B,C,的对边分别为a,b,c,若f(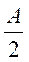 )=0,a=1,求△ABC面积的最大值。
)=0,a=1,求△ABC面积的最大值。
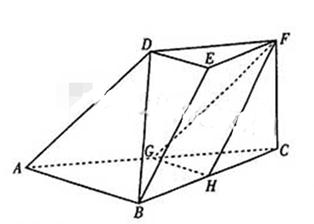 (17)(本小题满分12分)
(17)(本小题满分12分)
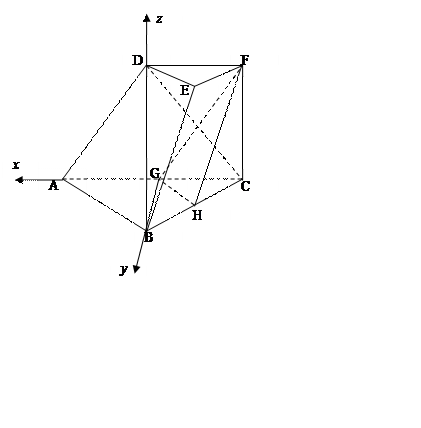
如图,在三棱台DEF-ABC中,
AB=2DE,G,H分别为AC,BC的中点。
(Ⅰ)求证:BC//平面FGH;
(Ⅱ)若CF⊥平面ABC,AB⊥BC,CF=DE, ∠BAC=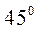 ,求平面FGH与平面ACFD所成的角(锐角)的大小.
,求平面FGH与平面ACFD所成的角(锐角)的大小.
(18)(本小题满分12分)
设数列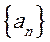 的前n项和为
的前n项和为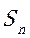 .已知2
.已知2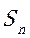 =
=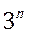 +3.
+3.
(I)求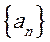 的通项公式;
的通项公式;
(II)若数列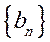 满足
满足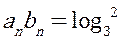 ,求
,求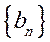 的前n项和
的前n项和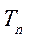 .
.
(19)(本小题满分12分)
若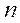 是一个三位正整数,且
是一个三位正整数,且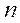 的个位数字大于十位数字,十位数字大于百位数字,则称
的个位数字大于十位数字,十位数字大于百位数字,则称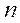 为“三位递增数”(如137,359,567等).
为“三位递增数”(如137,359,567等).
在某次数学趣味活动中,每位参加者需从所有的“三位递增数”中随机抽取1个数,且只能抽取一次.得分规则如下:若抽取的“三位递增数”的三个数字之积不能被5整除,参加者得0分;若能被5整除,但不能被10整除,得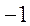 分;若能被10整除,得1分.
分;若能被10整除,得1分.
(I)写出所有个位数字是5的“三位递增数” ;
(II)若甲参加活动,求甲得分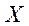 的分布列和数学期望
的分布列和数学期望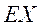 .
.
(20)(本小题满分13分)
平面直角坐标系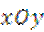 中,已知椭圆
中,已知椭圆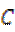 :
: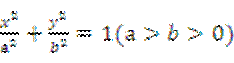 的离心率为
的离心率为 ,左、右焦点分别是
,左、右焦点分别是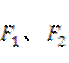 .以
.以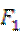 为圆心以3为半径的圆与以
为圆心以3为半径的圆与以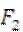 为圆心1为半径的圆相交,且交点在椭圆
为圆心1为半径的圆相交,且交点在椭圆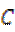 上.
上.
(Ⅰ)求椭圆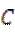 的方程;
的方程;
(Ⅱ)设椭圆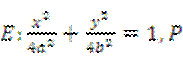 为椭圆
为椭圆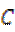 上任意一点,过点
上任意一点,过点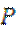 的直线
的直线 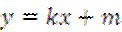 交椭圆
交椭圆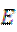 于
于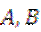 两点,射线
两点,射线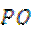 交椭圆
交椭圆 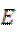 于点
于点 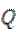 .
.
( i )求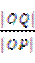 的值;
的值;
(ii)求△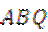 面积的最大值.
面积的最大值.
(21)(本小题满分14分)
设函数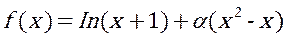 ,其中
,其中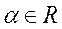 。
。
(Ⅰ)讨论函数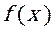 极值点的个数,并说明理由;
极值点的个数,并说明理由;
(Ⅱ)若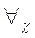 >0,
>0,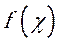
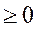 成立,求
成立,求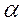 的取值范围。
的取值范围。
1C 2A 3B 4D 5A 6B 7C 8B 9D 10C
11. 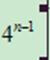 12. 1 13.
12. 1 13.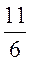 14.—
14.—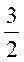 15.
15. 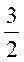
16. 解:(Ⅰ)由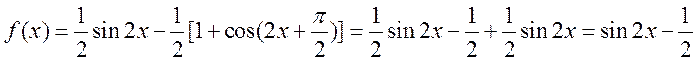
由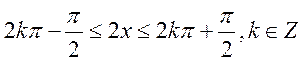 得
得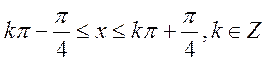 ,
,
则 的递增区间为
的递增区间为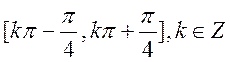 ;
;
由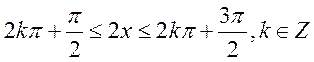 得
得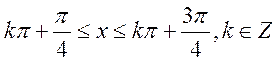 ,
,
则 的递增区间为
的递增区间为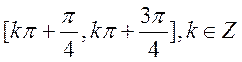 .
.
(Ⅱ)在锐角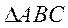 中,
中,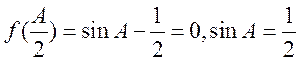 ,
,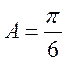 ,而
,而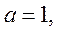
由余弦定理可得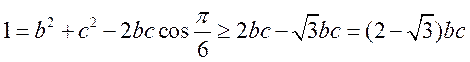 ,当且仅当
,当且仅当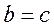 时等号成立,即
时等号成立,即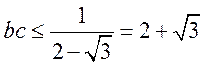 ,
,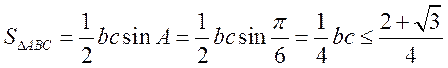 ,
,
故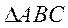 面积的最大值为
面积的最大值为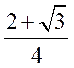 .
.
17. 解:(Ⅰ)证明:连接DG,DC,设DC与GF交于点T.
在三棱台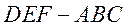 中,
中,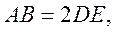 则
则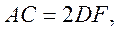
而G是AC的中点,DF//AC,则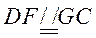 ,
,
所以四边形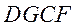 是平行四边形,T是DC的中点,DG//FC.
是平行四边形,T是DC的中点,DG//FC.
又在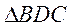 ,H是BC的中点,则TH//DB,
,H是BC的中点,则TH//DB,
 又
又 平面
平面 ,
, 平面
平面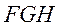 ,故
,故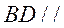 平面
平面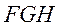 ;
;
(Ⅱ)由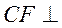 平面
平面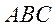 ,可得
,可得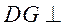 平面
平面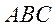 而
而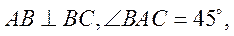
则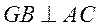 ,于是
,于是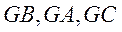 两两垂直,
两两垂直,
以点G为坐标原点,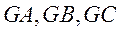 所在的直线
所在的直线
分别为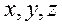 轴建立空间直角坐标系,
轴建立空间直角坐标系,
设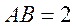 ,则
,则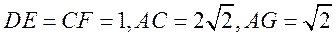 ,
,
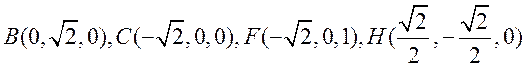 ,
,
则平面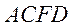 的一个法向量为
的一个法向量为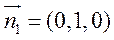 ,
,
设平面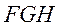 的法向量为
的法向量为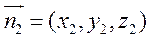 ,则
,则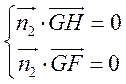 ,即
,即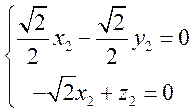 ,
,
取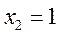 ,则
,则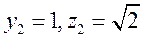 ,
,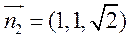 ,
,
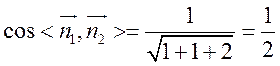 ,故平面
,故平面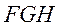 与平面
与平面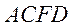 所成角(锐角)的大小为
所成角(锐角)的大小为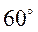 .
.
18. 解:(Ⅰ)由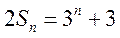 可得
可得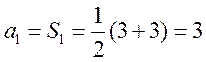 ,
,
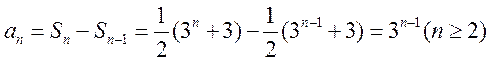
而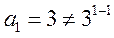 ,则
,则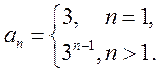
(Ⅱ)由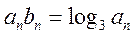 及
及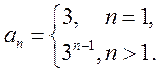 可得
可得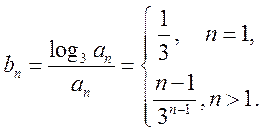
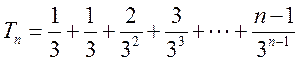 .
.
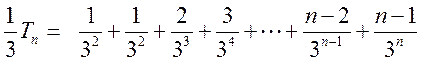
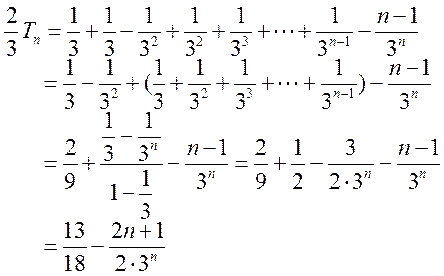
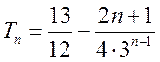
19. 解:(Ⅰ)125,135,145,235,245,345;
(Ⅱ)X的所有取值为-1,0,1.
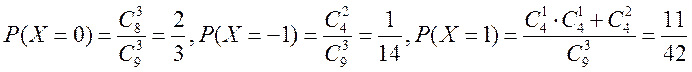
甲得分X的分布列为:
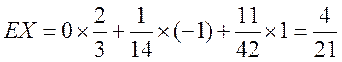
解析:(Ⅰ)由椭圆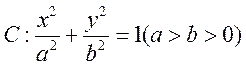 的离心率为
的离心率为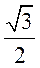 可知
可知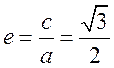 ,而
,而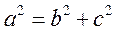 则
则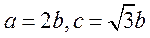 ,左、右焦点分别是
,左、右焦点分别是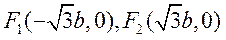 ,
,
圆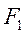 :
: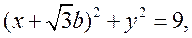 圆
圆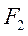 :
: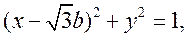 由两圆相交可得
由两圆相交可得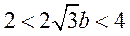 ,即
,即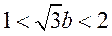 ,交点
,交点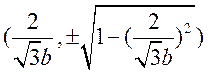 ,在椭圆C上,则
,在椭圆C上,则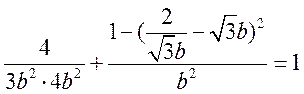 ,
,
整理得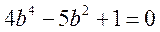 ,解得
,解得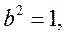
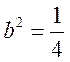 (舍去)
(舍去)
故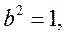
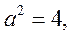 椭圆C的方程为
椭圆C的方程为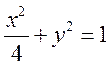 .
.
(Ⅱ)(ⅰ)椭圆E的方程为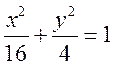 ,
,
设点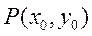 ,满足
,满足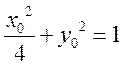 ,射线
,射线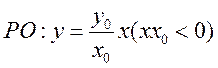 ,
,
代入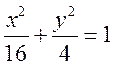 可得点
可得点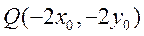 ,于是
,于是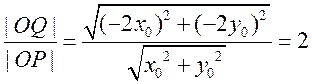 .
.
(ⅱ)点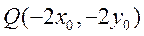 到直线
到直线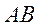 距离等于原点O到直线
距离等于原点O到直线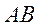 距离的3倍:
距离的3倍:
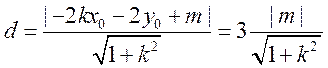
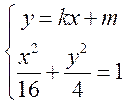 ,得
,得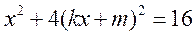 ,整理得
,整理得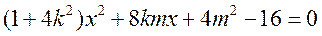
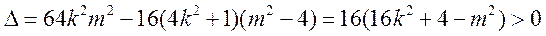
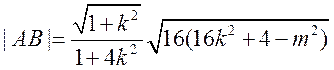
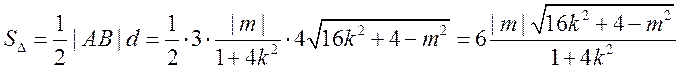
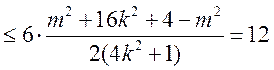 ,当且仅当
,当且仅当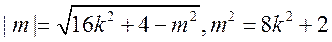 等号成立.
等号成立.
而直线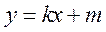 与椭圆C:
与椭圆C: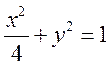 有交点P,则
有交点P,则
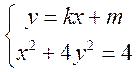 有解,即
有解,即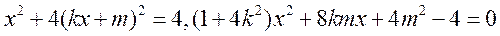 有解,
有解,
其判别式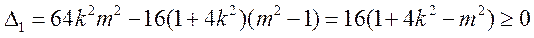 ,即
,即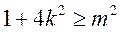 ,则上述
,则上述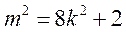 不成立,等号不成立,
不成立,等号不成立,
设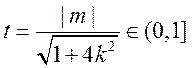 ,则
,则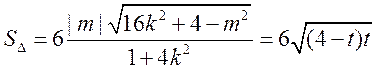 在
在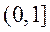 为增函数,
为增函数,
于是当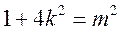 时
时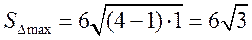 ,故
,故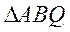 面积最大值为12.
面积最大值为12.
解:(Ⅰ)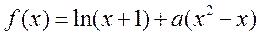 ,定义域为
,定义域为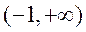
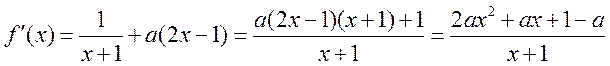 ,
,
设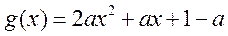 ,
,
当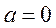 时,
时,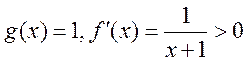 ,函数
,函数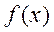 在
在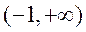 为增函数,无极值点.
为增函数,无极值点.
当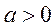 时,
时,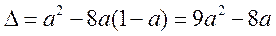 ,
,
若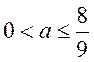 时
时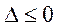 ,
,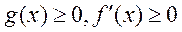 ,函数
,函数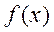 在
在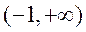 为增函数,无极值点.
为增函数,无极值点.
若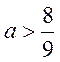 时
时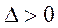 ,设
,设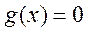 的两个不相等的实数根
的两个不相等的实数根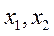 ,且
,且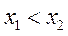 ,
,
且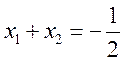 ,而
,而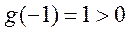 ,则
,则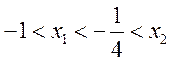 ,
,
所以当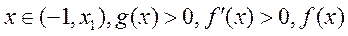 单调递增;
单调递增;
当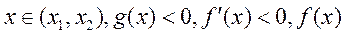 单调递减;
单调递减;
当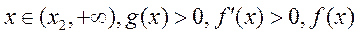 单调递增.
单调递增.
因此此时函数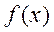 有两个极值点;
有两个极值点;
当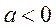 时
时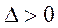 ,但
,但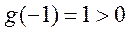 ,
,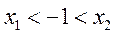 ,
,
所以当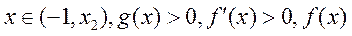 单调递増;
单调递増;
当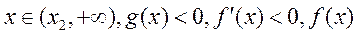 单调递减.
单调递减.
所以函数只有一个极值点。
综上可知当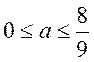 时
时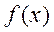 的无极值点;当
的无极值点;当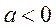 时
时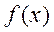 有一个极值点;当
有一个极值点;当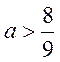 时,
时,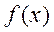 的有两个极值点.
的有两个极值点.
(Ⅱ)由(Ⅰ)可知当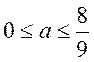 时
时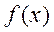 在
在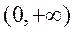 单调递增,而
单调递增,而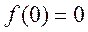 ,
,
则当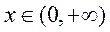 时,
时,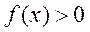 ,符合题意;
,符合题意;
当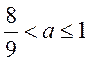 时,
时,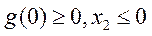 ,
,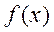 在
在