|
微信搜索关注"91考试网"公众号,领30元,获取公务员、事业编、教师等考试资料40G!
bsp; 经过点(1,1)且斜率为k的直线与椭圆E交于不同的两点P,Q(均异于点A),证明:直线AP与AQ的斜率之和为2.
21、(本小题满分12分)
设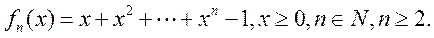
(I) 求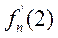 ; ;
(II) 证明: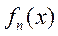 在(0, 在(0,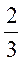 )内有且仅有一个零点(记为 )内有且仅有一个零点(记为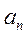 ),且0< ),且0<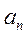 - - < <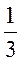 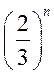 . .
考生注意:请在22、23、24三题中任选一题作答,如果多做,则按所做的第一题计分,作答时用2B铅笔在答题卡上把所选题目的题号后的方框涂黑.
22、(本小题满分10分)选修4-1:几何证明选讲
如图,AB切于 于点B,直线AO交 于点B,直线AO交 于D,E两点,BC 于D,E两点,BC DE,垂足为C. DE,垂足为C.
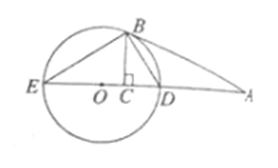
(I) 证明: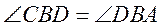 ; ;
(II) 若AD=3DC,BC=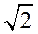 ,求 ,求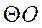 的直径. 的直径.
23、(本小题满分10分)选修4-1,坐标系与参数方程
在直角坐标系xOy中,直线l的参数方程为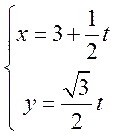 (t为参数).以原点为极点,x轴正半轴为极轴建立极坐标系, (t为参数).以原点为极点,x轴正半轴为极轴建立极坐标系,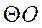 的极坐标方程为 的极坐标方程为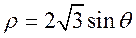 . .
(I) 写出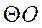 的直角坐标方程; 的直角坐标方程;
(II) P为直线l上一动点,当P到圆心C的距离最小时,求P的直角坐标.
24、(本小题满分10分)选修4-5,不等式选讲
已知关于x的不等式|x+a|<b的解集为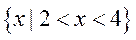 . .
(I) 求实数a,b的值.
(II) 求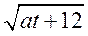 + +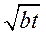 的最大值. 的最大值.
1
2
3
4
5
6
7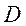
8
9
10
11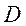
12
13、5
14.8
15.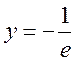
16.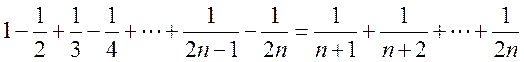
17.(I)因为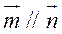 ,所以 ,所以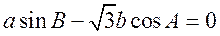
由正弦定理,得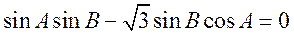 , ,
又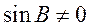 ,从而 ,从而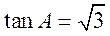 , ,
由于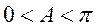
所以
(II)解法一:由余弦定理,得
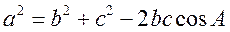 ,而 ,而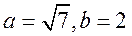 , , , ,
得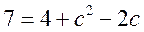 ,即 ,即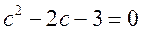
因为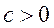 ,所以 ,所以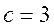 , ,
故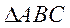 面积为 面积为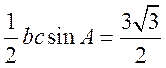 . .
解法二:由正弦定理,得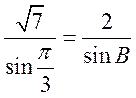
从而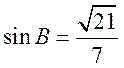
又由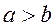 知 知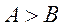 ,所以 ,所以
故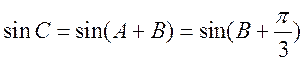
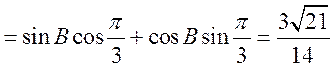 , ,
所以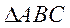 面积为 面积为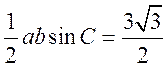 . .
18.
(II)由已知,平面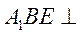 平面 平面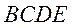 , ,
且平面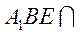 平面 平面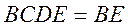
又由(I)知,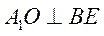 ,所以 ,所以
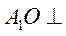 平面 平面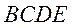 , ,
即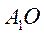 是四棱锥 是四棱锥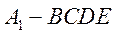 的高, 的高,
由图1可知,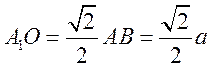 ,平行四边形 ,平行四边形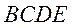 面积 面积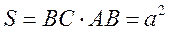 , ,
从而四棱锥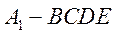 的为 的为
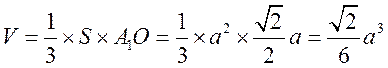 , ,
由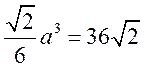 ,得 ,得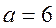 . .
19 (I)在容量为30的样本中,不下雨的天数是26,以频率估计概率,4月份任选一天,西安市不下雨的概率是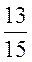 . .
(II)称相邻两个日期为“互邻日期对”(如1日与2日,2日与3日等)这样在4月份中,前一天为晴天的互邻日期对有16对,其中后一天不下雨的有14个,所以晴天的次日不下雨的频率为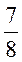 , ,
以频率估计概率,运动会期间不下雨的概率为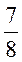 . .
考点:概率与统计.
20. (I)由题意知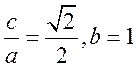 , ,
综合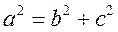 ,解得 ,解得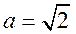 , ,
所以,椭圆的方程为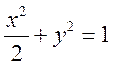 . .
(II)由题设知,直线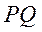 的方程为 的方程为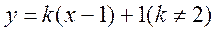 ,代入 ,代入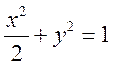 ,得 ,得
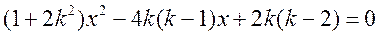 , ,
由已知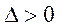 ,设 ,设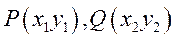 , ,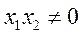
则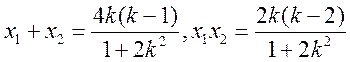 , ,
从而直线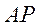 与 与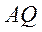 的斜率之和 的斜率之和
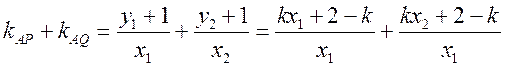
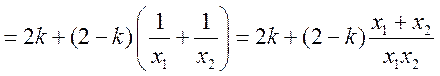
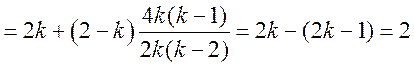 . .
21. (I)由题设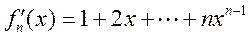 , ,
所以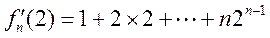 ① ①
由 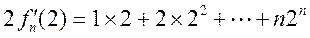 ② ②
①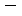 ②得 ②得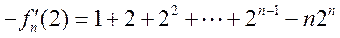
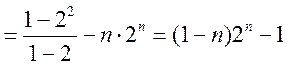 , ,
所以 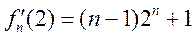
(II)因为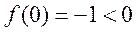
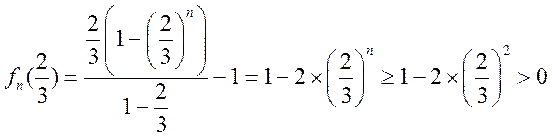 , ,
所以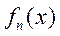 在 在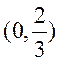 内至少存在一个零点, 内至少存在一个零点,
又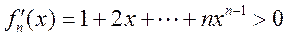
所以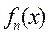 在 在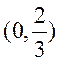 内单调递增, 内单调递增,
因此,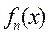 在 在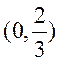 内有且只有一个零点 内有且只有一个零点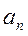 , ,
由于 , ,
所以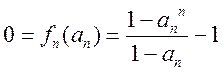
由此可得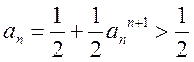
故
所以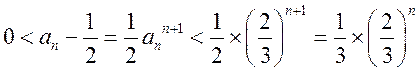
22. (I)因为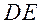 是 是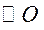 的直径, 的直径,
则
又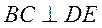 ,所以 ,所以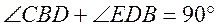
又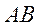 切 切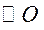 于点 于点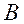 , ,
得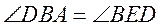
所以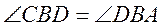
(II)由(I)知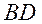 平分 平分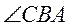 , ,
则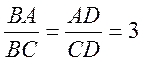 , ,
又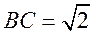 ,从而 ,从而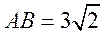 , ,
所以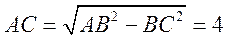
所以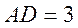 , ,
由切割线定理得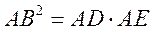
即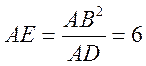 , ,
故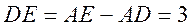 , ,
即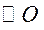 的直径为3. 的直径为3.
考点:1.几何证明;2.切割线定理.
23. (I)由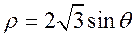 , ,
得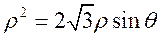 , ,
从而有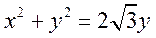
所以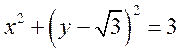
(II)设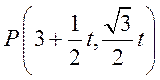 ,又 ,又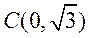 , ,
则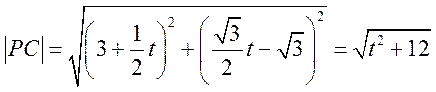 , ,
故当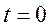 时, 时,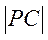 取得最小值, 取得最小值,
此时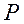 点的坐标为 点的坐标为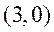 . .
考点:1. 坐标系与参数方程;2.点与圆的位置关系.
24. (I)由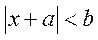 ,得 ,得
则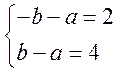 ,解得 ,解得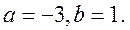
(II)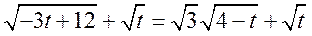
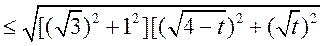
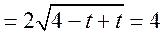
当且仅当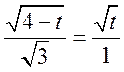 即 即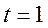 时等号成立, 时等号成立,
故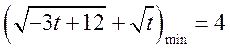
15、 
16、 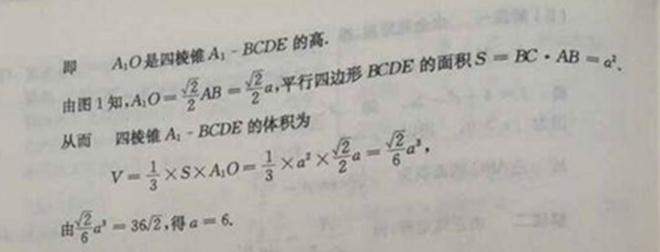
17、
18、 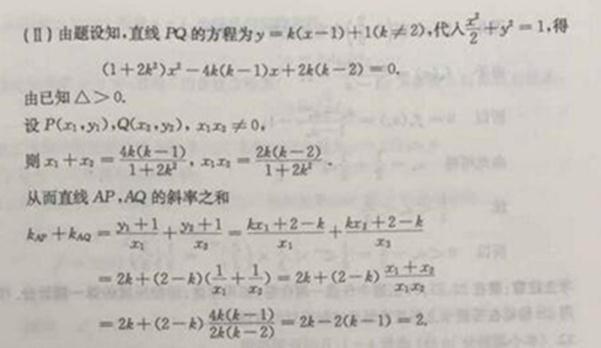
19、 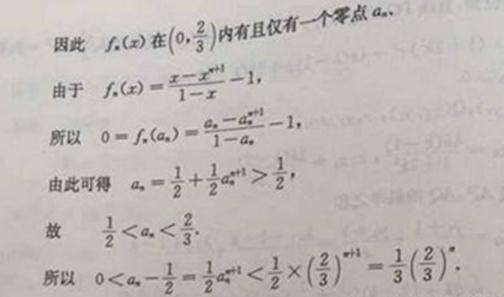
20、
21、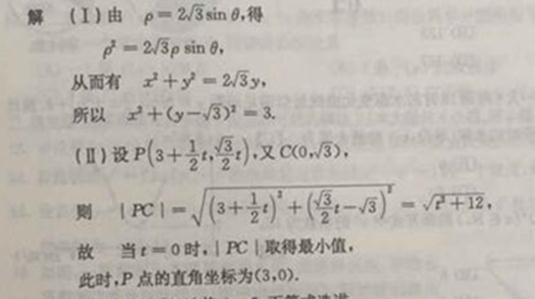
22、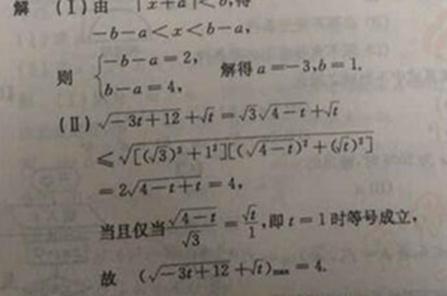
|