|
微信搜索关注"91考试网"公众号,领30元,获取公务员、事业编、教师等考试资料40G!
C.8 D.9
9.将函数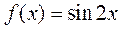 的图象向右平移 的图象向右平移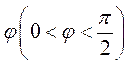 个单位后得到函数 个单位后得到函数 的图象,若对满足 的图象,若对满足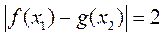 的 的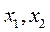 有 有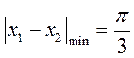 ,则 ,则 =( ) =( )
A.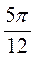 B. B. C. C.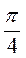 D. D.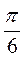
10.某工件的三视图如图3所示.现将该工件通过切割,加工成一个体积尽可能大的长方体新工件,并使新工件的一个面落在原工件的一个面内,则原工件材料的利用率为
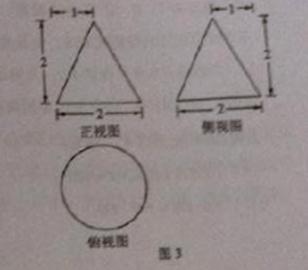 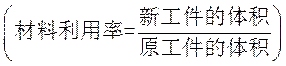
A. B. B.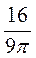
C.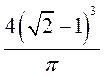 D. D. 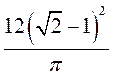
二、填空题:本小题共5小题,每小题5分,共25分.
11.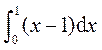 = . = .
12.在一次马拉松比赛中,35名运动员的成绩(单位:分钟)的茎叶图如图4所示:

若将运动员按成绩由好到差编为1~35号,再用系统抽样方法从中抽取7人,则其中成绩在区间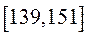 上的运动员人数是 . 上的运动员人数是 .
13.设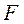 是双曲线 是双曲线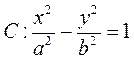 的一个焦点.若 的一个焦点.若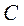 上存在点 上存在点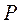 ,使线段 ,使线段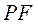 的中点恰为其虚轴一个端点,则 的中点恰为其虚轴一个端点,则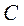 的离心率为 . 的离心率为 .
14.设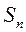 为等比数列 为等比数列 的前 的前 项和.若 项和.若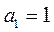 且 且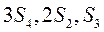 成等差数列,则 成等差数列,则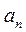 = . = .
15.已知函数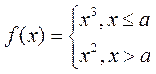 ,若存在实数 ,若存在实数 ,使函数 ,使函数 有两个零点,则 有两个零点,则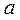 的取值范围是 . 的取值范围是 .
三、解答题:本大题共6小题,共75分,解答应写出文字说明,证明过程或演算步骤.
16.(本小题满分12分)
本小题设有I,II,III三个选做题,请考生任选两题作答,并将解答过程写在答题卡中相应题号的答题区域内.如果全做,则按所做的前两题计分.
I.(本题满分6分)选修4-1:几何证明选讲
如图5,在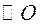 中,相交于点 中,相交于点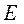 的两弦 的两弦 的中点分别是 的中点分别是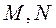 ,直线 ,直线 与直线 与直线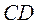 相交于 相交于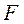 点,证明: 点,证明:
(i)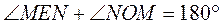 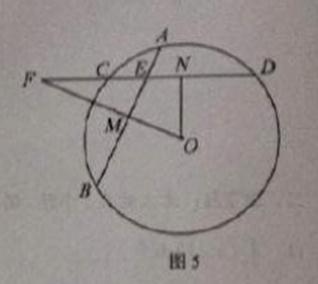
(ii)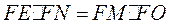
II.(本题满分6分)选修4-4:坐标系与参数方程
已知直线 ( (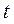 为参数).以坐标原点为极点, 为参数).以坐标原点为极点, 轴的正半轴为极轴建立极坐标系,曲线 轴的正半轴为极轴建立极坐标系,曲线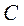 的极坐标方程为 的极坐标方程为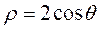
(i)将曲线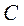 的极坐标方程化为直角坐标方程; 的极坐标方程化为直角坐标方程;
(ii)设点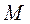 的直角坐标为 的直角坐标为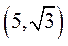 ,直线 ,直线 与曲线 与曲线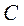 的交点为 的交点为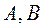 ,求 ,求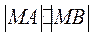 的值. 的值.
III.(本题满分6分)选修4-5,不等式选讲
设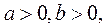 且 且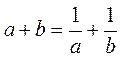 ,证明: ,证明:
(i)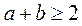
(ii)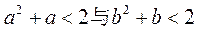 不可能同时成立. 不可能同时成立.
17.(本小题满分12分)
设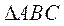 的内角 的内角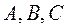 的对边分别为 的对边分别为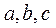 , ,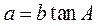 ,且 ,且 为钝角. 为钝角.
(I)证明: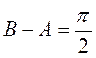 ; ;
(II)求 的取值范围. 的取值范围.
18.(本小题满分12分)
某商场举行有奖促销活动,顾客购买一定金额的商品后即可抽奖.每次抽奖都是从装有4个红球、6个白球的甲箱和装有5个红球、5个白球的乙箱中,各随机摸出1个球.在摸出的2个球中,若都是红球,则获一等奖;若只有1个红球,则获二等奖;若没有红球,则不获奖.
(I)求顾客抽奖1次能获奖的概率;
(II)若某顾客有3次抽奖机会,记该顾客在3次抽奖中获一等奖的次数为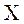 ,求 ,求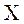 的分布列和数学期望. 的分布列和数学期望.
19.(本小题满分12分)
如图6,已知四棱台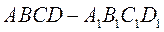 的上、下底面分别是边长为3和6的正方形. 的上、下底面分别是边长为3和6的正方形. 且 且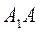 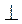 底面 底面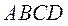 ,点 ,点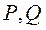 分别在棱 分别在棱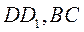 上. 上.
(I)若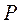 是 是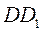 的中点,证明: 的中点,证明: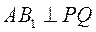
(II)若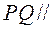 平面 平面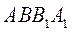 ,二面角 ,二面角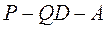 的余弦值为 的余弦值为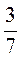 ,求四面体 ,求四面体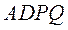 的体积. 的体积.
20.(本小题满分12分)
已知抛物线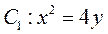 的焦点 的焦点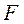 也是椭圆 也是椭圆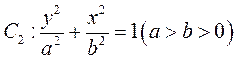 的一个焦点, 的一个焦点,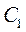 与 与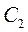 的公共弦的长为 的公共弦的长为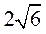 . .
(I)求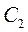 的方程; 的方程;
(II)过点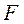 的直线 的直线 与 与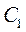 相交于 相交于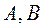 两点,与 两点,与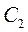 相交于 相交于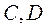 两点,且 两点,且 与 与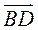 同向. 同向.
(i)若 ,求直线 ,求直线 的斜率; 的斜率;
(ii)设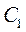 在点 在点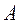 处的切线与 处的切线与 轴的交点为 轴的交点为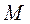 ,证明:直线 ,证明:直线 绕点 绕点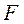 旋转时, 旋转时, 总是钝角三角形. 总是钝角三角形.
21.(本小题满分12分)
已知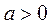 ,函数 ,函数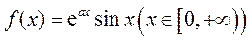 ,记 ,记 为 为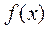 的从小到大的第 的从小到大的第 个极值点.证明: 个极值点.证明:
(I)数列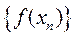 是等比数列; 是等比数列;
(II)若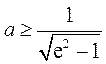 ,则对一切 ,则对一切 , ,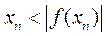 恒成立. 恒成立.
|