1.任意角、弧度制

（1）了解任意角的概念和弧度制的概念。

（2）能进行弧度与角度的互化。

例1．如图所示，在直角坐标系xOy中，射线OP交单位圆O于点P，若∠AOP＝θ，则点P的坐标是(　　)

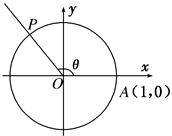
A．(cos θ，sin θ)　　　　　 B．(－cos θ，sin θ)

C．(sin θ，cos θ)                    D．(－sin θ，cos θ)

解析： 　由三角函数的定义知P(cos θ，sin θ)，

例2．已知扇形的周长是6 cm，面积是2 cm²，则扇形的圆心角的弧度数是(　　)

A．1或4    B．1   C．4    D．8

2.三角函数

（1）理解任意角三角函数（正弦、余弦、正切）的定义。

（2）能利用单位圆中的三角函数线推导出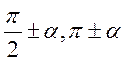的正弦、余弦、正切的诱导公式，能画出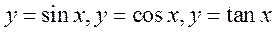的图像，了解三角函数的周期性。

（3）理解正弦函数、余弦函数在上的性质（如单调性、最大值和最小值、图像与坐标轴的交点等），理解正切函数在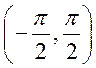内的单调性。

（4）理解同角三角函数的基本关系式：。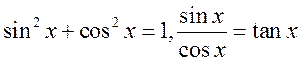

（5）了解函数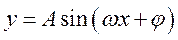的物理意义；能画出函数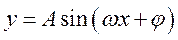的图像，了解参数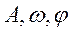对函数图像变化的影响。

（6）会用三角函数解决一些简单实际问题，体会三角函数是描述周期变化现象的重要函数模型。

例1．[2014·全国卷] 已知角α的终边经过点(－4，3)，则cos α＝(　　) 　

A.     B.    C．－     D．－

例2．[2014·新课标全国卷Ⅰ] 如图1­1，圆O的半径为1，A是圆上的定点，P是圆上的动点，角x的始边为射线OA，终边为射线OP，过点P作直线OA的垂线，垂足为M，将点M到直线OP的距离表示成x的函数f(x)，则y＝f(x)在[0，π]上的图像大致为(　　)   　

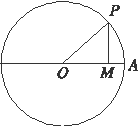
图1­1

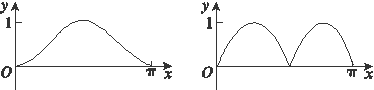
　　　                  A　 　　　 　　　　　B

　　　                   C　 　　　　　　　　D

例3．[2014·福建卷] 已知函数f(x)＝cos x(sin x＋cos x)－.

(1)若0<α<，且sin α＝，求f(α)的值；

(2)求函数f(x)的最小正周期及单调递增区间．

例4．[2014·新课标全国卷Ⅱ] 函数f(x)＝sin(x＋2φ)－2sin φcos(x＋φ)的最大值为________．　

例5．[2014·重庆卷] 已知函数f(x)＝sin(ωx＋φ)的图像关于直线x＝对称，且图像上相邻两个最高点的距离为π.

(1)求ω和φ的值；

(2)若f＝，求cos的值．

例6．[2014·四川卷] 为了得到函数y＝sin (2x＋1)的图像，只需把函数y＝sin 2x的图像上所有的点(　　)    　

A．向左平行移动个单位长度    B．向右平行移动个单位长度

C．向左平行移动1个单位长度   D．向右平行移动1个单位长度

例7．[2014·安徽卷] 若将函数f(x)＝sin的图像向右平移φ个单位，所得图像关于y轴对称，则φ的最小正值是________．　

例8．[2014·天津卷] 已知函数f(x)＝cos x·sin－cos²x＋，x∈R.

(1)求f(x)的最小正周期；

(2)求f(x)在闭区间上的最大值和最小值．

（九）平面向量

1.平面向量的实际背景及基本概念

（1）了解向量的实际背景

（2）理解平面向量的概念和两个向量相等的含义。

（3）理解向量的几何表示。

2.向量的线性运算

（1）掌握向量加法、减法的运算，理解其几何意义。

（2）掌握向量数乘的运算及其几何意义，理解两个向量共线的含义。

（3）了解向量线性运算的性质及其几何意义。

例1．[2014·福建卷] 设M为平行四边形ABCD对角线的交点，O为平行四边形ABCD所在平面内任意一点，则＋＋＋等于(　　)    

A.     B．2     C．3     D．4

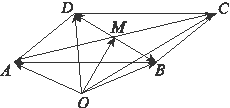
例2．[2014·全国新课标卷Ⅰ] 设D，E，F分别为△ABC的三边BC，CA，AB的中点，则＋＝(　　)    

A.       B.    C.      D.

3.平面向量的基本定理及坐标表示

（1）了解平面向量的基本定理及其意义。

（2）掌握平面向量的正交分解及其坐标表示。

（3）会用坐标表示平面向量的加法、减法与数乘运算。

（4）理解用坐标表示的平面向量共线的条件。

4.平面向量的数量积

（1）理解平面向量数量积的含义及其物理意义。

（2）了解平面向量的数量积与向量的投影的关系。

（3）掌握数量积的坐标表达式，会进行平面向量数量积的运算。

（4）能运用数量积表示两个向量的夹角，会用数量积判断两个平面向量的垂直关系。

例3．[2014·北京卷] 已知向量a＝(2，4)，b＝(－1，1)，则2a－b＝(　　) 　

A．(5，7)  B．(5，9)   C．(3，7)  D．(3，9)

例4．[2014·广东卷] 已知向量a＝(1，2)，b＝(3，1)，则b－a＝(　　) 　

A．(－2，1)  B．(2，－1)  C．(2，0)  D．(4，3)

例5．[2014·山东卷] 已知向量a＝(1，)，b＝(3，m)，若向量a，b的夹角为，则实数m＝(　　)    　

A．2    B.   C．0    D．－

例6．[2014·陕西卷] 在直角坐标系xOy中，已知点A(1，1)，B(2，3)，C(3，2)，点P(x，y)在 △ABC三边围成的区域(含边界)上，且＝m＋n(m，n∈R)．

(1)若m＝n＝，求||；

(2)用x，y表示m－n，并求m－n的最大值．

例7．[2014·全国卷] 已知a，b为单位向量，其夹角为60°，则(2a－b)·b＝(   ) 　

A．－1    B．0    C．1     D．2

例8．[2014·新课标全国卷Ⅱ] 设向量a，b满足|a＋b|＝，|a－b|＝，则a·b＝(　　) 　

A．1    B．2    C．3    D．5

5.向量的应用

（1）会用向量方法解决某些简单的平面几何问题。

（2）会用向量方法解决简单的力学问题与其他一些实际问题。

例1．[2014·湖南卷] 在平面直角坐标系中，O为原点，A(－1，0)，B(0，)，C(3，0)，动点D满足||＝1，则|＋＋|的最大值是________．　

例2．[2014·四川卷] 已知F为抛物线y²＝x的焦点，点A，B在该抛物线上且位于x轴的两侧，·＝2(其中O为坐标原点)，则△ABO与△AFO面积之和的最小值是(　　)  

A．2  B．3  C.  D.

例3．(2013·天津一中月考)在四边形ABCD中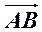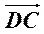，＝＝(1,1)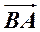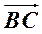，＋＝，则四边形ABCD的面积为________．

（十）三角恒等变换

1.两角和与差的三角函数公式

（1）会用向量的数量积推导出两角差的余弦公式。

（2）会用两角差的余弦公式推导出两角差的正弦、正切公式。

（3）会用两角差的余弦公式推导出两角的正弦、余弦、正切公式和二倍角的正弦、余弦、正切公式，了解它们的内在联系。

2.简单的三角恒等变换

    能运用上述公式进行简单的恒等变换（包括导出积化和差、和差化积、半角公式，但不要求记忆）。

例1．[2014·新课标全国卷Ⅱ] 函数f(x)＝sin(x＋2φ)－2sin φcos(x＋φ)的最大值为________．

例2．[2014·安徽卷] 设△ABC的内角A，B，C所对边的长分别是a，b，c，且b＝3，c＝1，A＝2B.

(1)求a的值；     (2)求sin的值．

（十一）解三角形

1.正弦定理和余弦定理

    掌握正弦定理、余弦定理，并能解决一些简单的三角形度量问题。

2.应用

   能够运用正弦定理、余弦定理等知识和方法解决一些与测量和几何计算有关的实际问题。

例1．[2014·辽宁卷] 在△ABC中，内角A，B，C的对边分别为a，b，c，且a>c.已知·＝2，cos B＝，b＝3.求：

(1)a和c的值；   (2)cos(B－C)的值．

例2． [2014·全国卷] △ABC的内角A，B，C的对边分别为a，b，c.已知3acos C＝2ccos A，tan A＝，求B.

（十二）数列

1.数列的概念和简单表示方法

（1）了解数列的概念和几种简单的表示方法（列表、图像、通项公式）。

（2）了解数列是自变量为正整数的一类特殊函数。

2．等差数列、等比数列

（1）理解等差数列、等比数列的概念。

（2）掌握等差数列、等比数列的通项公式与前n项和公式。

（3）能在具体的问题情境中识别数列的等差关系或等比关系，并能用等差数列、等比数列的有关知识解决相应的问题。

（4）了解等差数列与一次函数的关系、等比数列与指数函数的关系。

例1．[2014·重庆卷] 在等差数列{a_n}中，a₁＝2，a₃＋a₅＝10，则a₇＝(　　) 　

A．5  B．8  C．10  D．14

例2．[2014·天津卷] 设{a_n}是首项为a₁，公差为－1的等差数列，S_n为其前n项和．若S₁，S₂，S₄成等比数列，则a₁＝(　　)

A．2  B．－2    C.  D．－

例3．[2014·北京卷] 已知{a_n}是等差数列，满足a₁＝3，a₄＝12，数列{b_n}满足b₁＝4，b₄＝20，且{b_n－a_n}为等比数列．

(1)求数列{a_n}和{b_n}的通项公式；

(2)求数列{b_n}的前n项和．

例4．[2014·福建卷] 在等比数列{a_n}中，a₂＝3，a₅＝81.

(1)求a_n； &nbs