微信搜索关注"91考试网"公众号,领30元,获取公务员、事业编、教师等考试资料40G!
B运动时,满足于∠APQ=∠BPQ,试问直线AB的斜率是否为定值,请说明理由.
(十六)空间向量与立体几何
(1)了解空间向量的概念,了解空间向量的基本定理及其意义,掌握空间向量的正交分解及其坐标表示。
(2)掌握空间向量的线性运算及其坐标表示。
(3)掌握空间向量的数量积及其坐标表示,能用向量的数量积判断向量的共线和垂直。
(4)理解直线的方向向量及平面的法向量。
(5)能用向量语言表述线线、线面、面面的平行和垂直关系。
(6)能用向量方法证明立体几何中有关线面位置关系的一些简单定理(包括三垂线定理)。
(7)能用向量方法解决直线与直线、直线与平面、平面与平面的夹角的计算问题,了解向量方法在研究立体几何问题中的应用。
例1、已知l,m是不同的两条直线,α,β是不重合的两个平面,则下列命题中为真命题的是( )
A.若l⊥α,α⊥β,则l∥β B.若l⊥α,α∥β,m⊂β,则l⊥m
C.若l⊥m,α∥β,m⊂β,则l⊥α D.若l∥α,α⊥β,则l∥β
例2.已知P为△ABC所在平面外的一点,则点P在此三角形所在平面上的射影是△ABC垂心的充分必要条件是( )..
A.PA=PB=PC B.PA⊥BC,PB⊥AC
C.点P到△ABC三边所在直线的距离相等
D.平面PAB、平面PBC、平面PAC与△ABC所在的平面所成的角相等
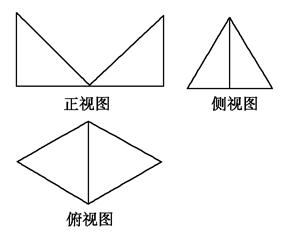 例3、如图所示是一个几何体的三视图,其侧视图是一个边长为a的等边三角形,俯视图是两个正三角形拼成的菱形,则该几何体的体积为( )
例3、如图所示是一个几何体的三视图,其侧视图是一个边长为a的等边三角形,俯视图是两个正三角形拼成的菱形,则该几何体的体积为( )
A.a3 B. C. D.
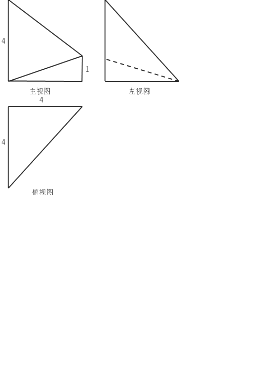 例4. 一个几何体的三视图如右图所示,则它的体积为( )
例4. 一个几何体的三视图如右图所示,则它的体积为( )
( )
A.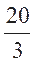 B.
B.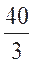 C.
C.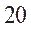 D.
D.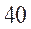
 例5. 某三棱锥的三视图如图所示,该三棱锥的体积是( )
例5. 某三棱锥的三视图如图所示,该三棱锥的体积是( )
A.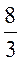 B. 4 C. 2 D.
B. 4 C. 2 D. 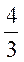
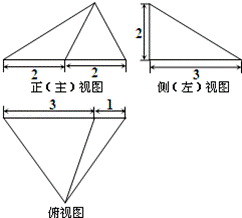
例6.若三棱锥的三视图如右图所示,则该三棱锥的体积为( )
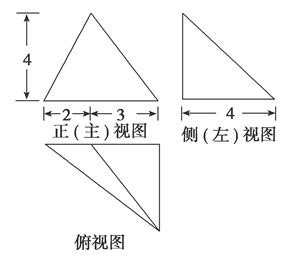 A.80 B.40 C. D.
A.80 B.40 C. D.
例7.一个多面体的三视图如图2所示,则此多面体外接球的表面积是 ( )
A. B.
B.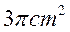 C.
C.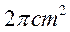 D.
D.
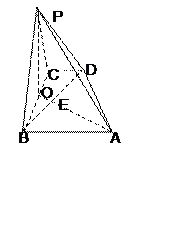 例8、如图,已知四棱锥
例8、如图,已知四棱锥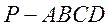 的底面是直角梯形,
的底面是直角梯形,
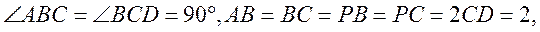
平面 平面
平面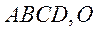 是
是 的中点,
的中点, 交
交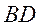 于点
于点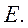
(1)求证: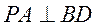 ;
;
(2)求证:平面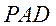
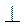 平面
平面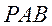 。
。
(十七)导数及其应用
(1)了解导数概念的实际背景。
(2)通过函数图象直观理解导数的几何意义。
(3)能根据导数的概念求函数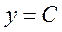
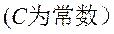 ,
,
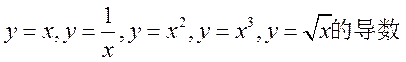 。
。
(4)能利用以下给出的基本初等函数的导数公式和导数的四则混合运算法则求简单函数的导数,并了解复合函数求导法则,能求简单复合函数(仅限于形如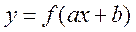 的复合函数)的导数。
的复合函数)的导数。
·常见的基本初等函数的导数公式:
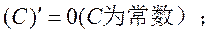
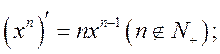

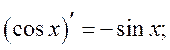
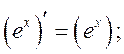
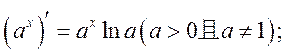
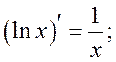
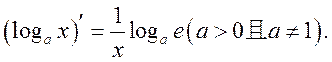
·常用的导数运算法则:
法则1: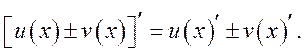
法则2: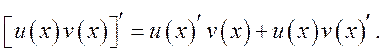
法则3: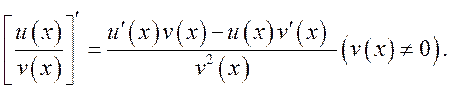
(5)了解函数的单调性与导数的关系;能利用导数研究函数的单调性;会求函数的单调区间(其中多项式函数不超过三次)。
(6)了解函数在某点取得极值的必要条件和充分条件;会用导数求函数的极大值、极小值(其中多项式函数不超过三次)。
(7)会用导数解决实际问题。
(8)了解定积分的实际背景,了解定积分的基本思想,了解定积分的概念。
(9)了解微积分基本定理的含义。
例1. (2013·北京东城模拟)根据表格中的数据,可以断定函数 f(x)=ln x-的零点所在的区间是( C )
|
x |
1 |
2 |
e |
3 |
5 |
|
ln x |
0 |
0.69 |
1 |
1.10 |
1.61 |
|
|
3 |
1.5 |
1.10 |
1 |
0.6 |
A. (1,2) B. (2,e) C. (e,3) D. (3,5)
例2. (2013·九江模拟)函数f(x)=ln(x-2)-的零点所在的大致区间是( )
A. (1,2) B. (2,3) C. (3,4) D. (4,5)
例3.(2013·安徽高考文科)已知函数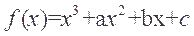 有两个极值点
有两个极值点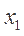 ,
,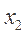 ,
,
若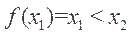 ,则关于
,则关于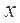 的方程
的方程 的不同实根个数是 ( )
的不同实根个数是 ( )
A.3 B.4 C. 5 D.6
例4.(2013·安徽高考理科)若函数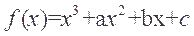 有极值点
有极值点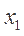 ,
,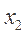 ,且
,且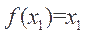 ,则关于
,则关于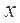 的方程
的方程 的不同实根个数是 ( )
的不同实根个数是 ( )
A.3 B.4 C. 5 D.6
例5. (2014·铜陵模拟)函数f(x)是R上的偶函数,且当x>0时,函数的解析式为f(x)=-1.
(1)用定义证明f(x)在(0,+∞)上是减函数;
(2)求当x<0时,函数的解析式.
例6. (2014·潍坊一中模拟)已知函数 f(x)=log4(4x+1)+kx(x∈R)是偶函数.
(1)求k的值;(2)若方程f(x)-m=0有解,求m的取值范围.
例7. (2014·淄博模拟)已知f(x)=ax-ln x,a∈R.
(1)当a=2时,求曲线f(x)在点(1,f(1))处的切线方程;
(2)若f(x)在x=1处有极值,求f(x)的单调递增区间;
(3)是否存在实数a,使f(x)在区间(0,e]的最小值是3?若存在,求出a的值;若不存在,请说明理由.
例8. 设函数f(x)=lnx-ax2-bx.
(1)当a=b=时,求f(x)的最大值;
(2)令F(x)=f(x)+ax2+bx+(0<x≤3),其图像上任意一点P(x0,y0)处的切线的斜率k≤恒成立,求实数a的取值范围.
(十八) 推理与证明
(1)了解合情推理的含义,能进行简单的归纳推理和类比推理,体会并认识合情推理在数学发现中的作用。
(2)了解演绎推理的含义,了解合情推理和演绎推理的联系和差异;掌握演绎推理的基本模式,并能运用它们进行一些简单的演绎推理。
(3)了解直接证明的两种基本方法:综合法和分析法;了解综合法和分析法的思考过程和特点。
(4)了解反证法的思考过程和特点。
(5)了解数学归纳法的原理,能用数学归纳法证明一些简单的数学命题。
例1.[2014·山东卷] 用反证法证明命题“设a,b为实数,则方程x2+ax+b=0至少有一个实根”时,要做的假设是( )
A. 方程x2+ax+b=0没有实根
B. 方程x2+ax+b=0至多有一个实根
C. 方程x2+ax+b=0至多有两个实根
D. 方程x2+ax+b=0恰好有两个实根
例2.[2014·北京卷] 学生的语文、数学成绩均被评定为三个等级,依次为“优秀”“合格”“不合格”.若学生甲的语文、数学成绩都不低于学生乙,且其中至少有一门成绩高于乙,则称“学生甲比学生乙成绩好”.如果一组学生中没有哪位学生比另一位学生成绩好,并且不存在语文成绩相同、数学成绩也相同的两位学生,那么这组学生最多有( )
A.2人 B.3人 C.4人 D.5人
(十九)数系的扩充与复数的引入
(1)理解复数的基本概念,理解复数相等的充要条件。
(2)了解复数的代数表示法及其几何意义,能将代数形式的复数在复平面上用点或向量表示。
(3)能进行复数代数形式的四则运算,了解两个具体复数相加、相减的几何意义。
例1.[2014·浙江卷] 已知i是虚数单位,a,b∈R,得“a=b=1”是“(a+bi)2=2i”的( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
例2.[2014·全国卷] 设z=,则z的共轭复数为( )
A.-1+3i B.-1-3i C.1+3i D.1-3i
例3.[2014·安徽卷] 设i是虚数单位,表示复数z的共轭复数.若z=1+i,则+i·=( )
A.-2 B.-2i C.2 D.2i
例4.[2014·北京卷] 复数=________.
例5.[2014·福建卷] 复数z=(3-2i)i的共轭复数z等于( )
A.-2-3i B.-2+3i C.2-3i D.2+3i