1、简答题  如图所示，有A、B两质量均为M的小车，在光滑水平面上以相同的速率v0在同一直线上相对运动，A车上有一质量为m的人至少要以多大的速度（对地）从A车跳到B车上，才能避免两车的相撞？

参考答案：速度v最小的条件是：人跳上A车稳定后两车的速度相等，以A车和人组成的系统为研究对象，以A车的初速度方向为正方向，由动量守恒定律得：
（M+m）v0=Mv车+mv，
以B车与人组成的系统为研究对象，以人的速度方向为正方向，由动量守恒定律得：
-Mv0+mv=（M+m）v车，
解得：v=（1+2M22Mm+m2）v0；
答：人至少要以（1+2M22Mm+m2）v0的速度（对地）从A车跳到B车上，才能避免两车的相撞．

本题解析：

本题难度：一般

2、选择题  物体以某一初速度从粗糙的斜面底端沿斜面上滑,物体滑到最高点后又返回到斜面底端,则下列说法正确的是(? )
A．上滑过程中重力的冲量大于下滑过程中重力的冲量
B．上滑过程中摩擦力的冲量与下滑过程中摩擦力的冲量大小相等
C．上滑过程中弹力的冲量为零
D．上滑、下滑过程中合外力冲量的方向相同

参考答案：D

本题解析：设上滑初速为v0,返回至出发点时速度为v,因为上滑时摩擦力方向与重力分力方向相同,而下滑时摩擦力方向与重力分力方向相反,所以上滑时加速度大,时间短,则上滑过程中重力冲量小,A错.上滑过程中摩擦力冲量小,B错.上、下滑过程中合外力方向沿斜面向下,所以冲量方向相同,D对.

本题难度：简单

3、简答题  如图所示，甲、乙两光滑圆轨道放置在同一竖直平面内，甲轨道半径是R且为乙轨道半径的2倍，两轨道之间由一光滑水平轨道CD相连，在水平轨道CD上有一轻弹簧被a、b两个小球夹住，但不拴接．如果a、b两个小球的质量均为m，同时释放两小球，且要求a、b都能通过各自的最高点，则弹簧在释放前至少具有多大的弹性势能？

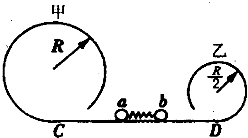
参考答案：当a球恰能通过最高点时，b球一定通过最高点，此时弹簧在释放前具有的弹性势能最小，设a球到达圆轨道最高点的速度为va，对于a球有：
mag=mav2aR…①
设a球被弹簧弹开瞬间的速度为v"a，对于a球由机械能守恒定律可得：12mav′2a=12mav2a+mag2R… ②
设b球被弹簧弹开瞬间的速度为v"b，由于a、b两球被弹开时系统动量守恒：mav"a=mbv"b …③
①②③可得：v′a=v′b=

本题解析：

本题难度：一般

4、计算题  (10分) 如图所示，质量M＝40 g的靶盒A静止在光滑水平导轨上的O点，水平轻质弹簧一端拴在固定挡板P上，另一端与靶盒A连接，Q处有一固定的发射器B，它可以瞄准靶盒发射一颗水平速度v0＝50 m/s、质量m＝10 g的弹丸．当弹丸打入靶盒A后，便留在盒内，碰撞时间极短，不计空气阻力．弹丸进入靶盒A后，弹簧的最大弹性势能为多少？

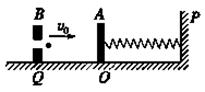
参考答案：2.5J

本题解析：
弹丸进入靶盒后，设弹丸与靶盒A的共同速度为v，由系统动量守恒定律mv0="(m+M)v"
靶盒A 的速度减为零时，弹簧的弹性势能最大 ，由机械能守恒定律可得：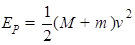
解得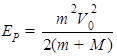：，代入数据得：EP=2.5J

本题难度：一般

5、简答题  如图，质量为m的小船甲在静止在水面上，一质量为

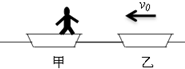
参考答案：设两船恰好不相撞，最后具有共同速度v1，以乙船的初速度方向为正方向，由动量守恒定律：
(2m+m3)v1=mv0
人从甲船跃出的过程动量守恒，乙船的速度方向为正方向，由动量守恒定律得：
0=mv1+13m(-v+v1)，
解得：v=127v0；
答：速率v至少为127v0才能避免两船相撞．

本题解析：

本题难度：简单