1、选择题  

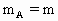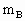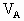如图所示，A、B为两个装有条形磁铁的小车，在光滑水平木板上沿一直线相向运动，已知，=2m，=V，=2V，设两磁铁始终不接触，则当它们相距最近时，A的速度为

参考答案：B

本题解析：
A、B组成的系统动量守恒，取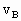方向为正，当它们相距最近时是相对静止的，即具有相同速度，设该速度为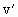，则：


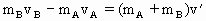
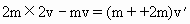
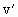=v，说明A的速度大小为v，与原来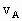方向相反．

本题难度：简单

2、简答题  将带电量Q=0．3 C，质量m′=0．15 kg的滑块，放在小车的绝缘板的右端，小车的质量M=0．5 kg，滑块与绝缘板间的动摩擦因数μ=0．4，小车的绝缘板足够长，它们所在的空间存在着磁感应强度B="20" T的水平方向的匀强磁场，开始时小车静止在光滑水平面上，当一个摆长为L=1．25 m，摆球质量m=0．4 kg的单摆从水平位置由静止释放，摆到最低点时与小车相撞，如图所示，碰撞后摆球恰好静止，g取10 m/s2．求：

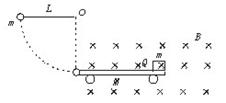
（1）摆球与小车碰撞过程中系统损失的机械能E是多少？
（2）碰撞后小车的最终速度是多少？

参考答案：（1）ΔE=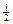mv2－Mv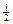12="1.31J?" （2）v2/=1.2m/s

本题解析：（1）由机械能守恒定律得：mgL=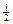mv2，?
代入L、g解得v =" 5m/s" 。
在m碰撞M的过程中，由动量守恒定律得：
mv－Mv1 = 0，
代入m、M解得v1=1.5m/s
ΔE=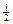mv2－Mv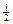12=1.31J
（2）假设m′最终能与M一起运动，由动量守恒定律得：
Mv1=（M+m′）v2
代入m′、M解得v2 = 0.9375m/s
m′以v2=0.83m/s速度运动时受到的向上洛仑兹力f = BQv2=5.625N＞m/g=3N
所以m′在还未到v2=0.9375m/s时已与M分开了。由上面分析可知当m′的速度为v3=3/（0.3×20）=0.5m/s时便与M分开了，根据动量守恒定律可得方程：
Mv1 = Mv2/+m/v3?解得v2/=1.2m/s

本题难度：简单

3、计算题  如图所示，已知水平面上的P点右侧光滑，左侧与滑块间的动摩擦因数为μ。质量分别为m1和m2的两个滑块在水平面上P点的右侧分别以速度v1、v2向右运动，由于V1>V2而发生碰撞(碰撞前后两滑块的速度均在一条直线上)。二者碰后m1继续向右运动，m2被右侧的墙以原速率弹回，再次与m1相碰，碰后m2恰好停止，而m1最终停在Q点。测得PQ间的距离为L。求第一次碰后滑块m1的速度。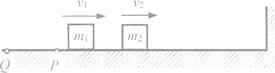

参考答案：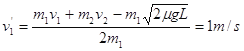

本题解析：根据动量守恒定律有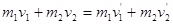?①? (3分)
第二次碰撞?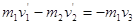?② (3分)
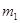过P点向左运动过程中，由动能定理得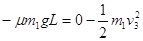?③(2分)
解得：?④ (2分

本题难度：简单

4、选择题  如图所示，质量分别为m和2m的A、B两物块用轻弹簧相连，放在光滑水平面上，A靠紧竖直墙。现用力F向左缓慢退物块B压缩弹簧，当力F做功为W时，突然撤去F，在A物体开始运动以后，弹簧弹性势能的最大值是

A.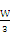?B.?
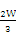C.?D.W

参考答案：A

本题解析：撤去F，在A物体开始运动以后，A在加速，B在减速，A、B间的距离在增大，当A、B间距离最大时，二者速度相等，此时弹簧有最大弹性势能。撤去F，系统机械能守恒，由题意可知，系统总的机械能为W。在A开始离开墙壁时，弹簧处于原长，此时B物体的动能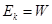为，动量为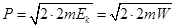，此后动量守恒。弹簧有最大弹性势能时，根据动量守恒有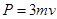，所以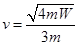，此时系统的动能为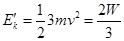，弹簧最大弹性势能。
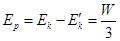故选A
点评：本题要注意哪个阶段开始机械能守恒，哪个阶段开始动量守恒，并且要知道机械能在各个时刻存在的形式。

本题难度：一般

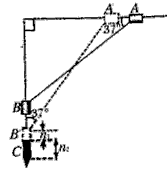
5、计算题  某机械打桩机原理可简化为如图所示，直角固定杆光滑，杆上套有mA=55kg和mB=80kg两滑块，两滑块用无弹性的轻绳相连，绳长为5m，开始在外力作用下将A滑块向右拉到与水平夹角为37°时静止释放，B滑块随即向下运动带动A滑块向左运动，当运动到绳子与竖直方向夹角为37°时，B滑块（重锤）撞击正下方的桩头C，桩头C的质量mC=200kg。碰撞时间极短，碰后A滑块由缓冲减速装置让其立即静止，B滑块反弹上升h1=0.05m，C桩头朝下运动h2=0.2m静止。取g=10m/s2。求：
（1）滑块B碰前的速度；
（2）泥土对桩头C的平均阻力。

参考答案：解：（1）设碰前A的速度为vA，B的速度为vB，由系统机械能守恒定律：

物体A和物体B沿绳的分速度相等：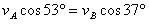
联立以上两式得：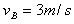
（2）B与C碰撞动量守恒：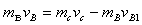
B碰后竖直上抛：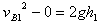
联立以上两式得：
对C用动能定理：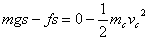
所以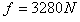

本题解析：

本题难度：困难