1、选择题  质量不计的弹簧下端固定一小球。现手持弹簧上端使小球随手在竖直方向上以同样大小的加速度a（a＜g）分别向上、向下做匀加速直线运动。若忽略空气阻力，弹簧的伸长分别为x1、x2；若空气阻力不能忽略且大小恒定，弹簧的伸长分别为、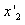。则
[? ]
A．
B．
C．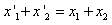
D．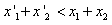

参考答案：A

本题解析：

本题难度：一般

2、计算题  2008年5月12日，四川汶川地区发生8级特大地震，给人民生命和财产造成极大危害。危急关头，在党和政府的积极指挥下，英雄的消防官兵及时地出现在灾区人民面前，为他们排忧解难。在一次救援行动中，一名消防队员沿着长为12m的竖立在地面上的钢管往下滑。这名队员的质量为60kg，他从钢管顶端由静止开始先匀加速再匀减速下滑，滑到地面时速度恰好为零。如果加速时的加速度大小是减速时的加速度大小的2倍，下滑的总时间为3s，那么该消防队员下滑过程中的最大速度是多少？加速和减速下滑时，消防队员与钢管间的摩擦力之比是多少？

参考答案：解：设最大速度为Vm，由S=Vmt／2 得：Vm=8m／s
又Vm=a1t1=a2t2
由题意a1=2a2，t=t1+ t2=3
则t1=1s，t2=2s，a1=8m／s2，a2=4m／s2
mg－f1=ma1
且f2－mg=ma2
则f1=l20N，f2=840N
所以f1：f2=1：7

本题解析：

本题难度：困难

3、计算题  如图(a)所示，质量m=1 kg的物体沿倾角θ=37°的固定粗糙斜面由静止开始向下运动，风对物体的作用力沿水平方向向右，其大小与风速v成正比，比例系数用k表示，物体的加速度a与风速v的关系如图(b)所示， （sin37°=0.6，cos37°=0.8，g取10 m/s2）求：
(1)物体与斜面间的动摩擦因数μ；
(2)比例系数k。

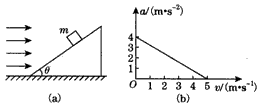
参考答案：解：(1)由题图知v=0时，a0=4 m/s2
由牛顿第二定律得：mgsinθ-μmgcosθ=ma0
解得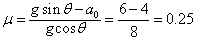
(2)由题图知v=5m/s时，a=0
由平衡条件得：mgsinθ-μFN-kvcosθ=0，FN=mgcosθ十kvsinθ
联立两式得：mg(sinθ-μcosθ)-kv(μsinθ+cosθ)=0
解得k=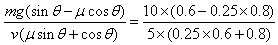kg/s=0.84 kg/s

本题解析：

本题难度：困难

4、简答题  在海滨游乐场里有一种滑沙运动，如图所示，人坐在滑板上从斜坡的高处A点由静止开始滑下，滑到斜坡底端B点后沿水平的滑道再滑行一段距离到C点停下来．若某人和滑板的总质量m=60.0kg，滑板与斜坡滑道和水平滑道间的动摩擦因数均为μ=0.50，斜坡的倾角θ=37°（sin37°=0.6，cos37°=0.8），斜坡与水平滑道间是平滑连接的，整个运动过程中空气阻力忽略不计，重力加速度g取10m/s2．求：
（1）人从斜坡上滑下的加速度为多大？
（2）若由于场地的限制，水平滑道的最大距离BC为L=20.0m，则人在斜坡上滑下的距离AB应不超过多少？

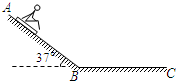
参考答案：（1）人在斜面上受力如图所示，建立图示坐标系，设人在斜坡上滑下的加速度为a1

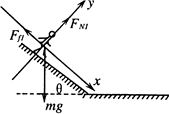
由牛顿第二定律有 mgsinθ-Ff1=ma1
FN1-mgcosθ=0
又 Ff1=μFN1
联立解得　a1=g（sinθ-μcosθ）=2.0 m/s2
（2）根据动能定理，选取从开始到停止，
则有：mgLABsinθ-μmgL-μmgcosθLAB=0-0；
解得：LAB=50m；
答：（1）人从斜坡滑下的加速度为2m/s2；（2）若由于场地的限制，水平滑道的最大距离为L=20.0m，则人在斜坡上滑下的距离AB应不超过50m．

本题解析：

本题难度：一般

5、简答题  如图所示，A为放在气垫导轨（气垫导轨是一种常见的实验仪器，它是利用气泵使带孔的导轨与滑块之间形成气垫，使滑块浮在导轨上，滑块在导轨上的运动可看作没有摩擦）上的滑块，B为砝码，某同学用此装置来探究物体运动的加速度a与所受外力F的关系.保持滑块的质量M不变，通过增减砝码个数来改变细绳对滑块拉力F的大小；再借助光电计时器、光电门等测得有关数据，从而计算出滑块的加速度a,并将实验数据记入下表.


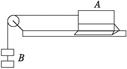
该同学在分析表中的实验数据时发现：对于前三组数据，砝码的重力G跟滑块加速度a的比值近似等于一个常数（即a随G的增大而正比例增大）；而后三组数据，砝码的重力G跟滑块加速度a的比值则存在明显的差异（即a随G的增大不成正比例增大）.通过分析列式说明造成这一情况的原因.

参考答案：当砝码质量m远小于滑块质量M时，F≈mg=G,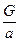≈M=常量（故前三组数据基本反映a∝F的关系）；当m接近M时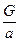，=M+m≠常量（故后三组数据不能反映a∝F的关系）.

本题解析：根据牛顿运动定律，对滑块有F=Ma
对砝码有：mg-F=ma,从而可得F=.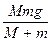
可知：当砝码质量m远小于滑块质量M时，F≈mg=G,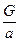≈M=常量（故前三组数据基本反映a∝F的关系）；当m接近M时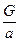，=M+m≠常量（故后三组数据不能反映a∝F的关系）.

本题难度：简单