1、计算题  用如图8-6-6所示装置验证动量守恒定律，质量为mA的钢球A用细线悬挂于O点，质量为mB的钢球B放在离地面高度为H的小支柱N上,O点到A球球心的距离为l，使悬线在A球释放前绷紧，且线与竖直线的夹角为α，A球释放后摆动到最低点（初始位置是水平的）时恰好与B球正碰，碰撞后，A球把轻质指示针OC推移到与竖直方向夹角β处，B球落在地面上，地面上铺一张盖有复写纸的白纸D，保持α角不变，多次重复上述实验，白纸上记录到多个B球的落点.

图8-6-6
（1）图中s应是B球初始位置到_________的水平距离.
（2）为了验证两球碰撞过程动量守恒，应测得_________等物理量.
（3）用测得的物理量表示碰撞前后A球、B球的动量：pA=_____，pA′=_________,pB=_______,pB′=_________.

参考答案：(1)落地点
(2)mA、mB、α、β、H、s、L
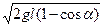(3)mAmA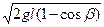? 0? mBs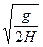

本题解析：图中s应是B球初始位置到落地点的水平距离.
碰前A球到最低点时的速度满足mvA2=mgl(1-cosα)
pA=mAvA=mA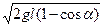
B球：pB=0
碰后：mvA′2=mgl(1-cosβ)
pA′=mAvA′=mA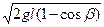
vB′=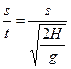,pB′=mBs.

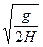本题难度：简单

2、选择题  如图所示，质量相等的A、B两小物块在光滑水平面上沿同一直线同向运动，动量分别为pA="8.0" kg·m/s，pB="4.0" kg·m/s.A追上B并与B相碰，碰后A、B的动量分别为pA′和pB′，pA′、pB′的值可能为(? )

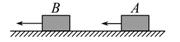
A.pA′=pB′="6.0" kg·m/s?
B.pA′="9.0" kg·m/s，pB′="3.0" kg·m/s
C.pA′="-2.0" kg·m/s，pB′="14.0" kg·m/s?
D.pA′="-4.0" kg·m/s，pB′="17.0" kg·m/s

参考答案：A

本题解析：本题考查的是动量守恒定律的问题，两个物块质量相等，相向运动，相碰之后任何一个物块的动量不可能超过碰前其中一个物块的动量，故只有A符合；

本题难度：简单

3、填空题  质量为100kg的小船静止在水面上，船两端有质量40kg的甲和质量60kg的乙，当甲、乙同时以3m/s的速率向左、向右跳入水中后，小船的速度大小为     m/s，方向是       。

参考答案：0.6m/s,向左

本题解析：规定向左为正，小船和两人组成的系统，动量守恒，故有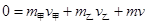，代入数据可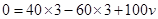得：，解得，速度为正，说明向正方向运动，
考点：考查了动量守恒定律的应用

本题难度：一般

4、选择题  质量相等的A、B两球在光滑水平面上沿同一直线运动，A球的动量是7kg·m/s，B球的动量是3kg·m/s，当A球追上B球时发生碰撞，则碰撞后A、B两球的动量可能值是
A．PA=5kg·m/s，PB= 5kg·m/s? B．PA=6kg·m/s，PB=4kg·m/s
C．PA=-2kg·m/s，PB=12kg·m/s? D．PA=-4kg·m/s，PB=17kg·m/s

参考答案：A

本题解析：本题考查的是动量守恒定律等问题，两球相碰满足动量守恒，如果开始是同向运动，两球质量相等，则碰后动量相等，A选项符合实际情况，如果开始是反向运动，两球质量相等，则碰后动量仍然相等，都是2kg·m/s，故只有A选项正确；

本题难度：一般

5、计算题  如图所示，半径为R，内表面光滑的半球形容器放在光滑的水平面上，容器左侧靠着竖直墙壁，一个质量为m的小球，从容器顶端A无初速释放，小球能沿球面上升的最大高度距球面底部B的距离为3R/4，小球的运动在竖直平面内。求：
（1）容器的质量M
（2）竖直墙作用于容器的最大冲量。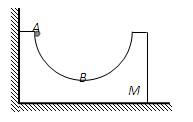

参考答案：（1）在A球释放到B点时，M未动，对A由机械能守恒有：
mgR=mv02（2分）
此后A继续向右运动，但B在A给它作用力情况下，离开墙壁向右运动，
对A、B系统：由水平方向动量守恒得：
mv0="(M+m)" v1（2分）
由机械能守恒得：
mg·R=mv02－(M+m) v12（2分）
由以上三式解得v0=?M=3m（2分）
（2）由于在A球释放到B点时，M未动，此后M离开墙壁向右运动，所以对A、B系统来讲，由动量定理知，竖直墙对容器的最大冲量为A球水平动量的变化，
即Im=mv0
代入v0得Im=m（2分）

本题解析：略

本题难度：一般