微信搜索关注"91考试网"公众号,领30元,获取公务员、事业编、教师等考试资料40G!
1、选择题 在光滑水平面上,一质量为m、速度大小为v的A球与质量为2m静止的B球碰撞后,A球的速度方向与碰撞前相反.则碰撞后B球的速度大小可能是
A.0.6v
B.0.4v
C.0.3v
D.0.2v
参考答案:A
本题解析:由动量守恒定律得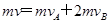 ,规定A球原方向为正方向,由题意可知vA为负值,则
,规定A球原方向为正方向,由题意可知vA为负值,则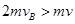 ,因此B球的速度可能为
,因此B球的速度可能为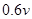 ,故选A。
,故选A。
本题难度:简单
2、简答题 如图,水平足够长光滑固定直杆AB上穿有质量为M的滑块,其上用光滑铰链着一个长为L的轻杆,杆的另一端固定着一个质量为M的小球,初始时,系统静止,轻杆水平。
小题1:1给小球以竖直向上的初速v01,球到达最高点时杆与水平方向呈θ角,(θ<900),求v01。
小题2:2给小球以竖直向上的初速v02,球到达最高点时的速度为v,求v02。
 ?
?
参考答案:
小题1: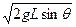 ?
?
小题2: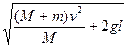
本题解析:
小题1:此题中须弄清的几个问题是,小球上升过程中,滑块是向左还是向右运动;小球到达最高点时是否有速度;此时滑块的速度方向如何;我们不妨这样来分析,若没有杆连接,则滑块不动,且小球将竖直向上运动。即最初杆有被拉伸的趋势。则滑块将向左运动。运动中小球和滑块在水平方向上不受外力,所以系统水平方向上动量守恒,①问中,假设小球在最高点时有水平向左的速度,则由水平方向动量守恒得滑块将有向右的速度,则上面的分析可知,滑块向左运动中出现向右的速度这是不可能的;若小球在最高点时有向左的速度,则由水平方向动量守恒可知,这时滑块将具有水平向左的速度,二者速度相反,则小球还是要上升,那么此时的位置就不是最高的;若小球具有向上或向下的速度,即小球处于上升或下降的过程中,则小球此时的位置也不是最高的。
 ①问中小球在最高点时不可能有速度。即速度为0,则由系统水平方向动量守恒得滑块此时的速度也是0,
①问中小球在最高点时不可能有速度。即速度为0,则由系统水平方向动量守恒得滑块此时的速度也是0,
则由系统机械能守恒(并非小球的机械能守恒)
得?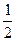 mv012=mgLsinθ,?解得v01=
mv012=mgLsinθ,?解得v01=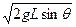 ?
?
小题2:2问中小球在最高点时的速度不为0,即小球到达最高点时轻杆竖直且速度向右。
由水平方向动量守恒得
mv-Mvx=0
又由系统机械能守恒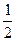 mv022=mgL+
mv022=mgL+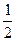 mv2+
mv2+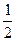 Mvx2
Mvx2
以上两式联立,可解得v02=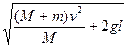
本题难度:简单
3、选择题 在光滑水平面上,两球沿球心连线以相等速率相向而行,下列现象可能的是(?)
A.若两球质量相等,碰后以某一相等速率互相分开
B.若两球质量相等,碰后以某一相等速率同向而行
C.若两球质量不同,碰后以某一相等速率互相分开
D.若两球质量不同,碰后以某一相等速率同向而行
参考答案:AD
本题解析:整体动量为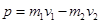
当两球质量相等时,总动量为零,碰撞总动量为零就是可能的,A对B错
若两球质量不等,设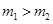 ,则
,则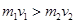 ,总动量与
,总动量与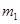 速度
速度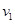 同向,当碰后以某一相等速率分开,
同向,当碰后以某一相等速率分开,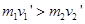 。则总动量方向一定与
。则总动量方向一定与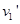 同向而与
同向而与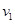 反向,不遵守动量守恒,不可能,C错
反向,不遵守动量守恒,不可能,C错
若两球质量不等,碰后粘合在一起有共同速度v运动,是可能的。D正确
正确答案AD
点评:基础题,难度适中,关键是紧扣碰撞前后动量守恒判断分析
本题难度:一般
4、计算题 如图所示,质量均为m的小车与木箱紧挨着静止在光滑的水平冰面上,质量为2m的小明站在小车上用力向右迅速推出木箱,木箱相对于冰面的速度为v,接着木箱与右侧竖直墙壁发生弹性碰撞,反弹后被小明接住,求小明接住木箱后三者共同速度的大小。

参考答案:v/2
本题解析:取向左为正方向,根据动量守恒定律 有推出木箱的过程:
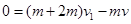 ? 1分
? 1分
接住木箱的过程: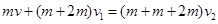 ?1分
?1分
解得 共同速度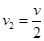 ? 2分
? 2分
本题难度:一般
5、选择题 如图所示,现有甲、乙两滑块,质量分别为3m和m,以相同的速率v在光滑水平面上相向运动,发生碰撞。已知碰撞后,甲滑块静止不动,则
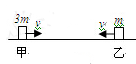
A.碰撞前总动量是4mv
B.碰撞过程动量不守恒
C.碰撞后乙的速度大小为2v
D.碰撞属于非弹性碰撞